Basics of Neural Network - Perceptron Model
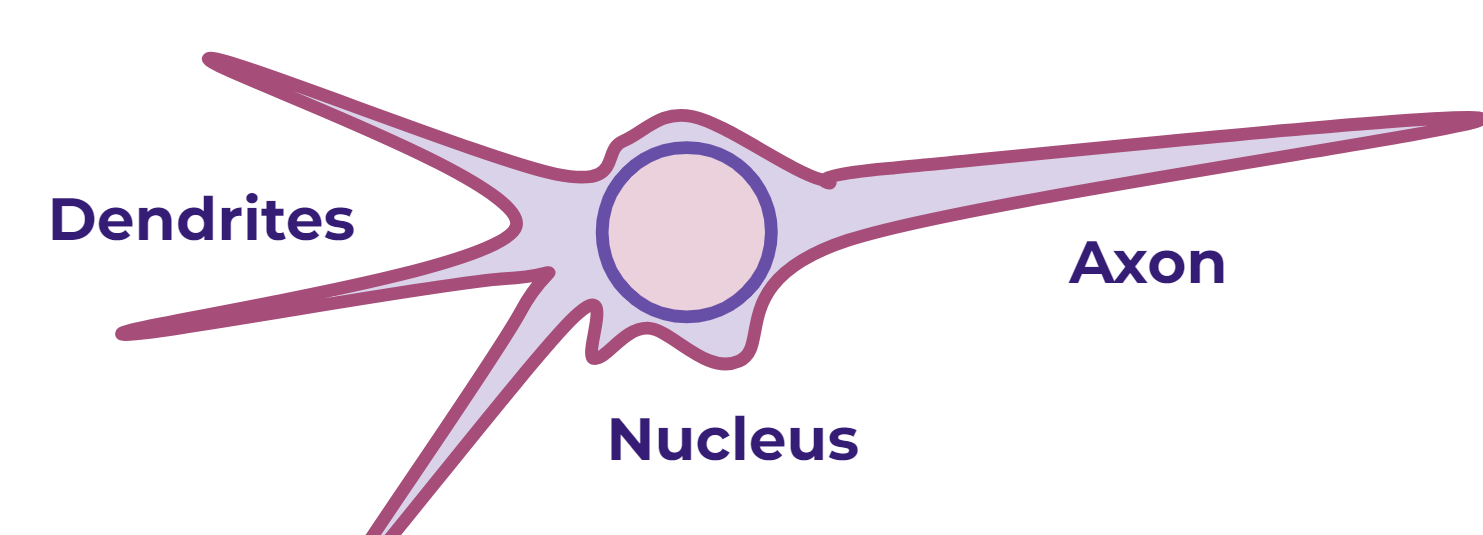
Biological Neurons
- Dendrites : inputs going into nucleus
- Nucleus : does the calculation
- Axon : passes output to other neurons
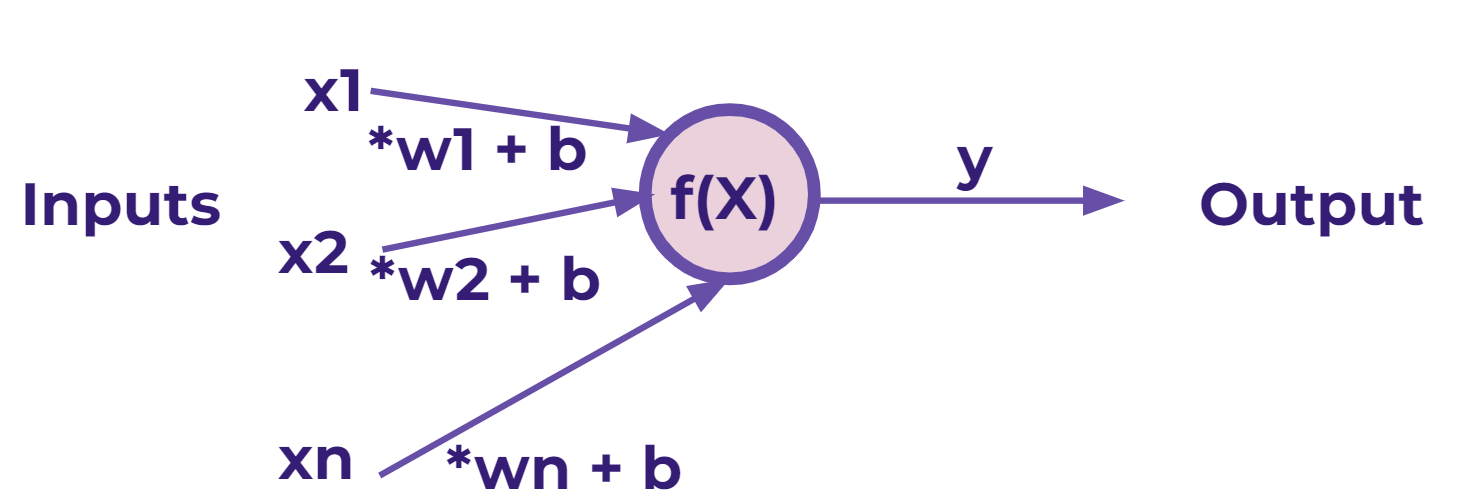
Perceptron Models
-
Neural Networks mimic this model
-
Generalized formula for perceptrons
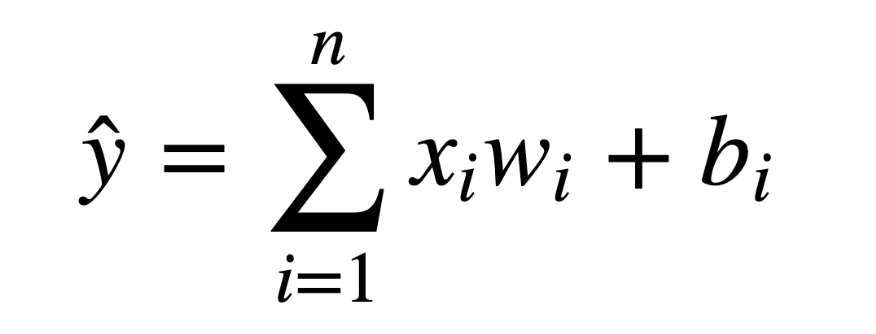
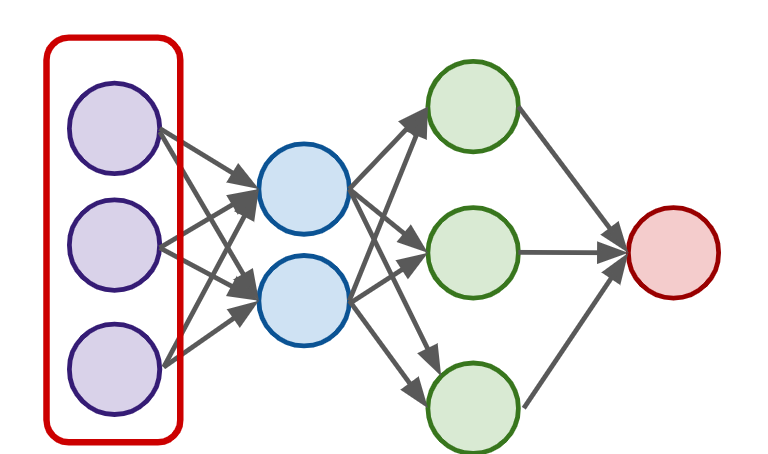
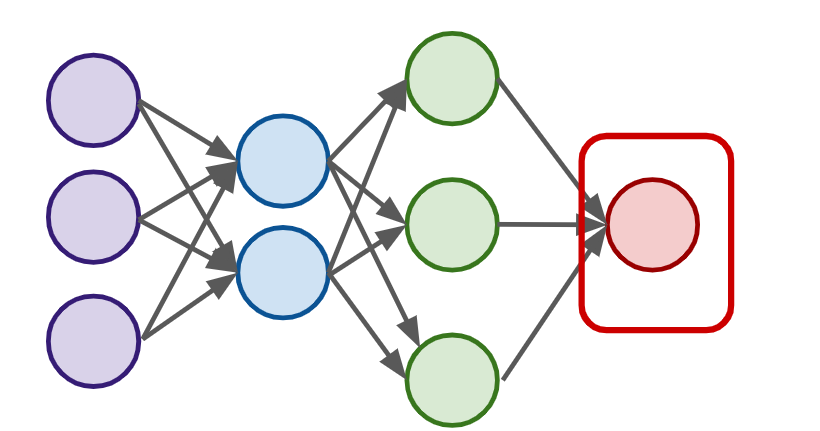
Neural Networks
- A single perceptron won’t be enough to learn complicated systems.
- To build a network of perceptrons, we can connect layers of perceptrons, using a multi-layer perceptron model.
-
Input Layer
-
Output Layer : final estimate of the output
- There could be multiple output layers
-
Hidden Layer : the layers in the middle
- Deep Network : 2 or more hidden layers
- Might be difficult to interpret
Activation Functions
-
z = x*w + b: basic formula for each perceptron
-w: how much weight or strength to give the incoming input
-b: an offset value, makingx*whave to reach a certain threshold before having an effect -
Activation Function (
f(z) or X) : sets boundaries to output values from the neuron -
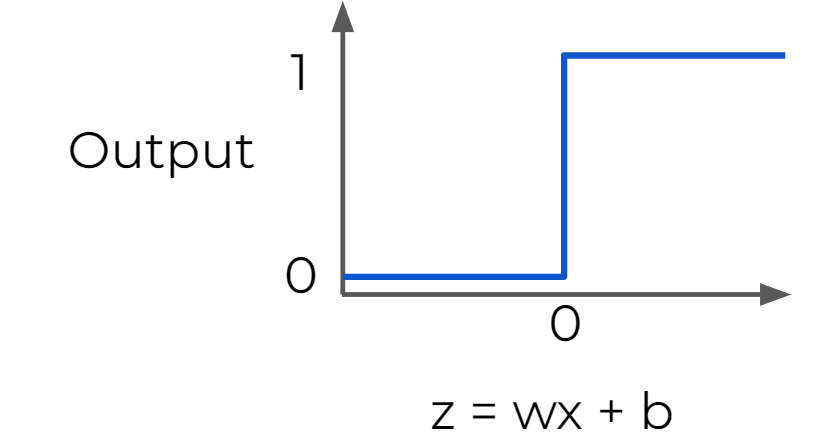
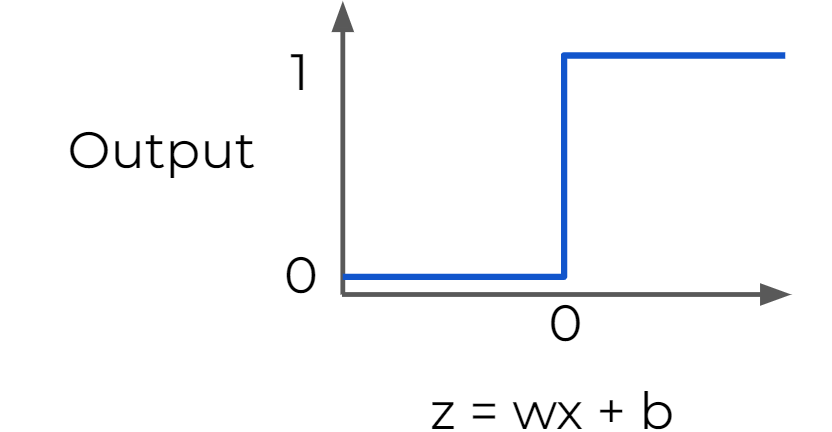
Step Function : Useful for classification
- a strong function - small changes aren't reflected
-
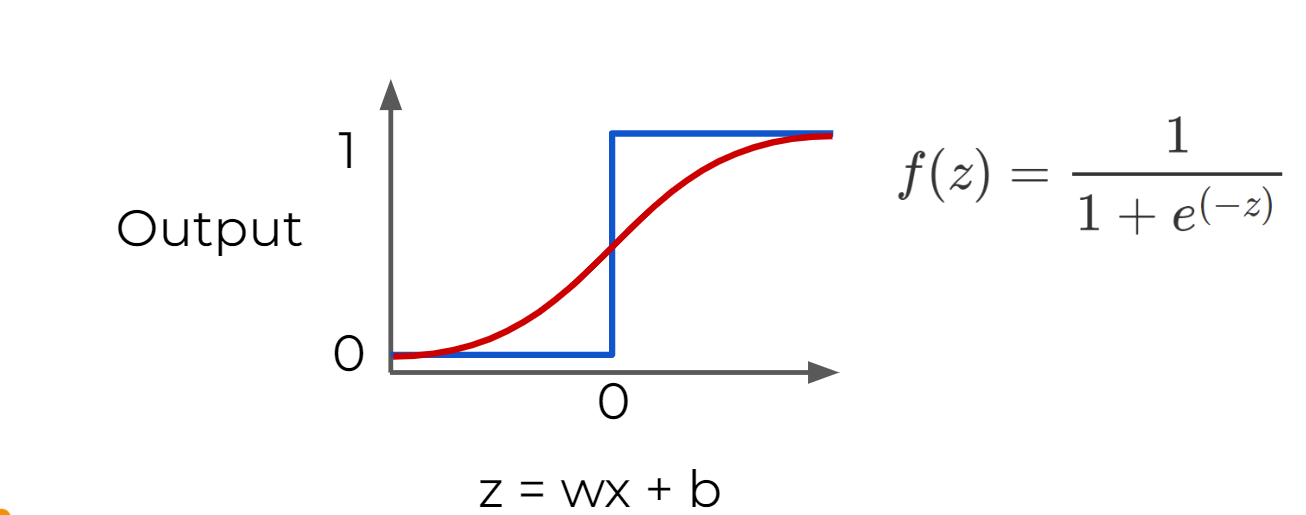
Sigmoid Function : moderate form of a step function
- more sensitive to small changes
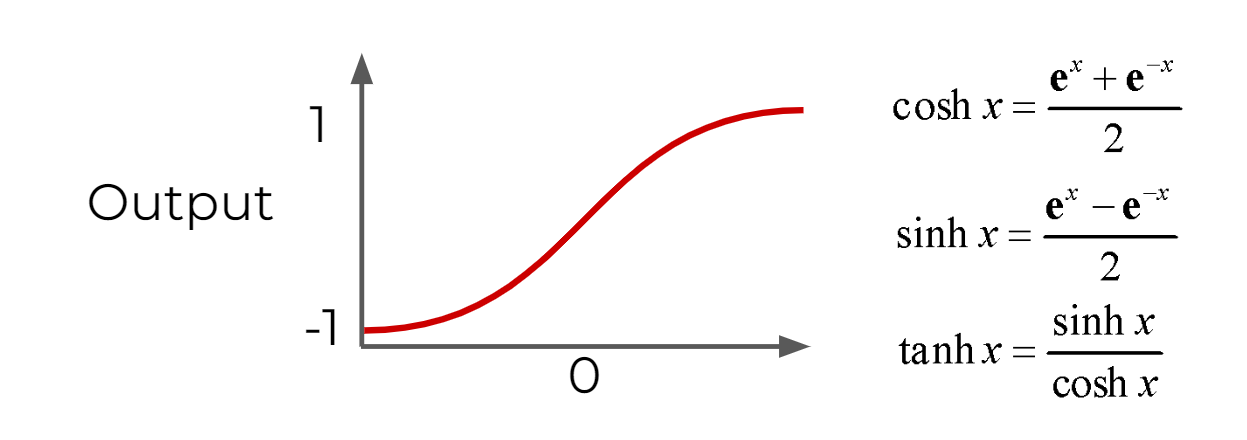
- Hyperbolic Tangent : outputs between -1 and 1
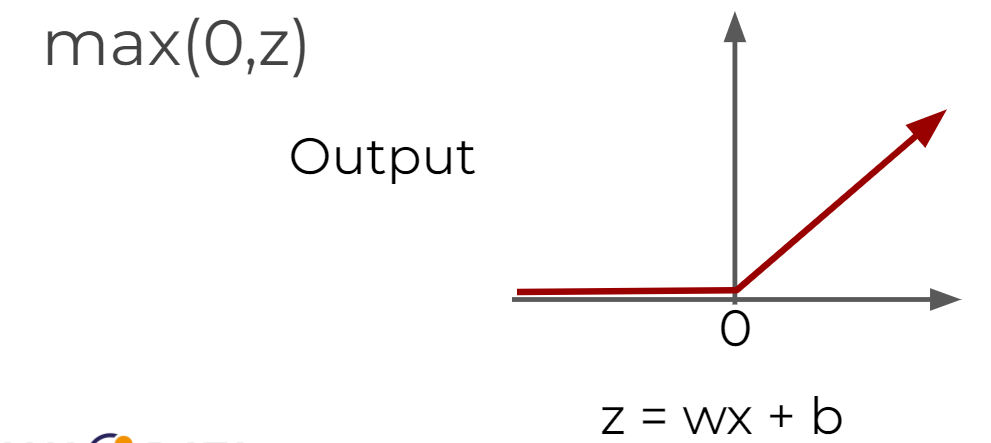
- Rectified Linear Unit (ReLU) :
max(0,z)
- deals with the issue of vanishing gradient
- usually used as the default activation function
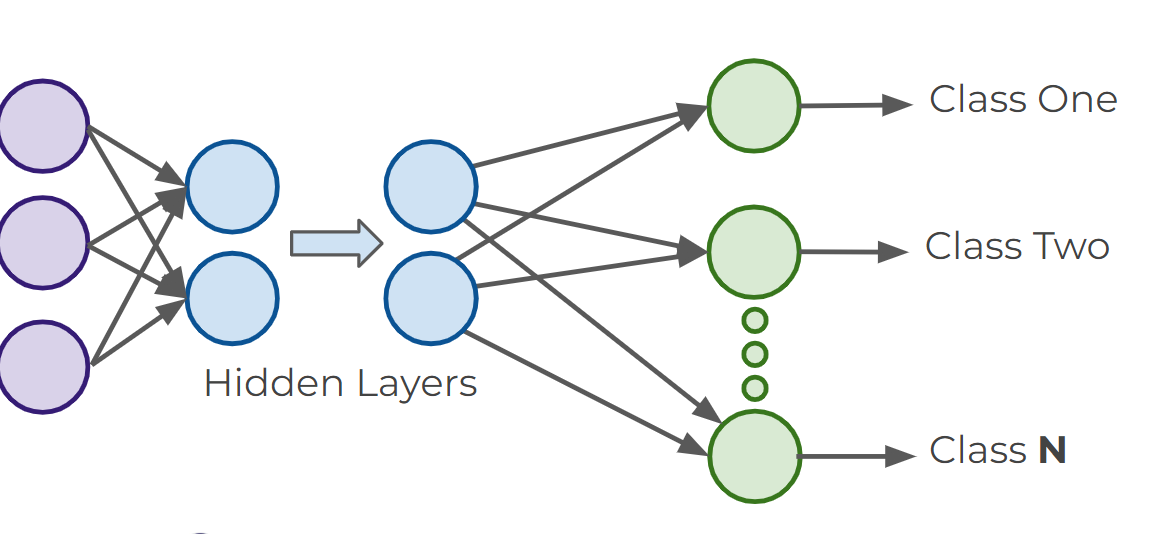
Multiclass Classifications
- There are 2 types of multi-class situations:
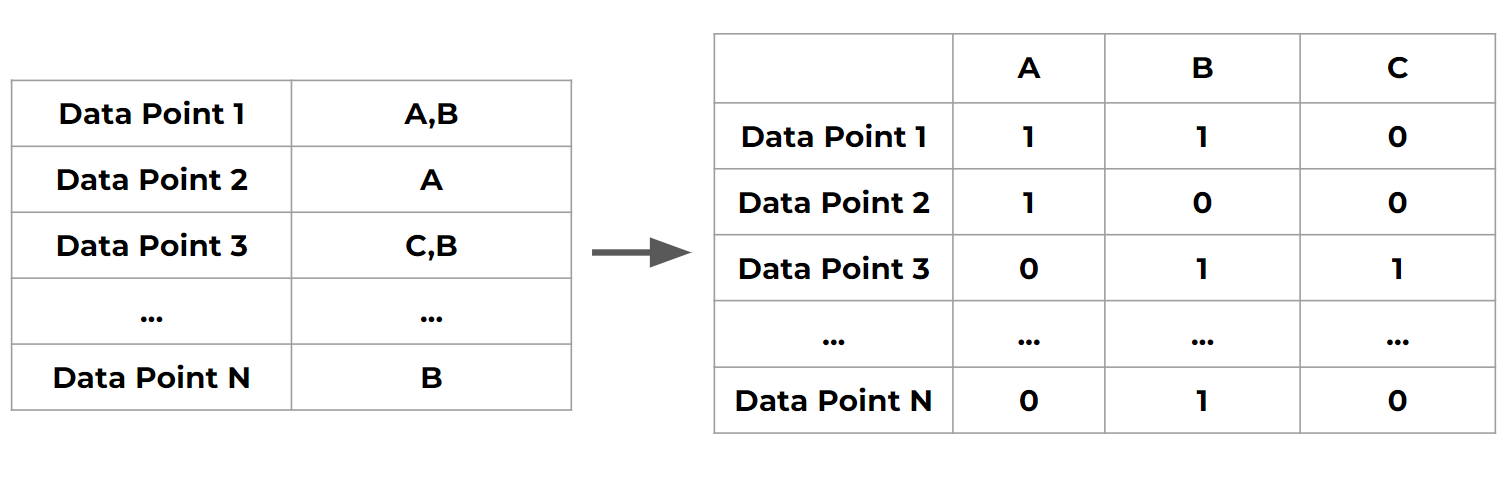
- Non-exclusive classes : a data point can have multiple classes/ categories assigned to it (e.g. tagging photos )
- Mutually Exclusive Classes : only one class per data point
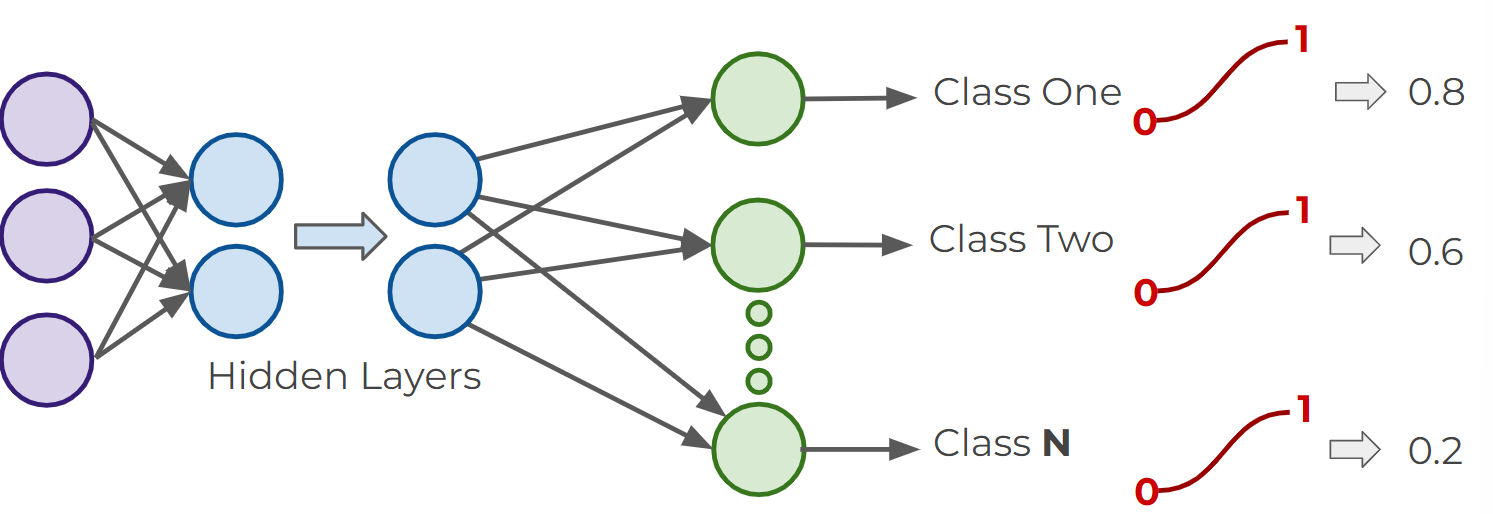
- For multiclass classifications, arrange multiple output layers
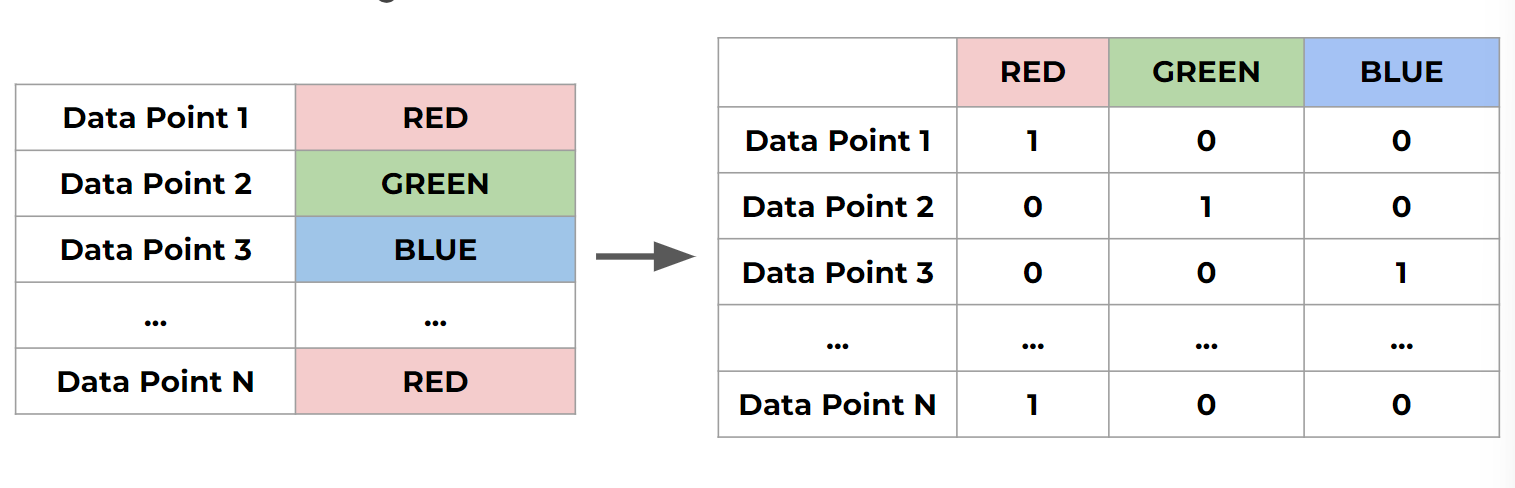
- One-hot encoding : how to turn classes into vectors
- Mutually Exclusive Classes
- Non-exclusive classes
-
Activation functions for multiclass classification (Non-exclusive)
-
Activation functions for multiclass classification (Exclusive)
- Softmax Function : the target class chosen will have the highest probability
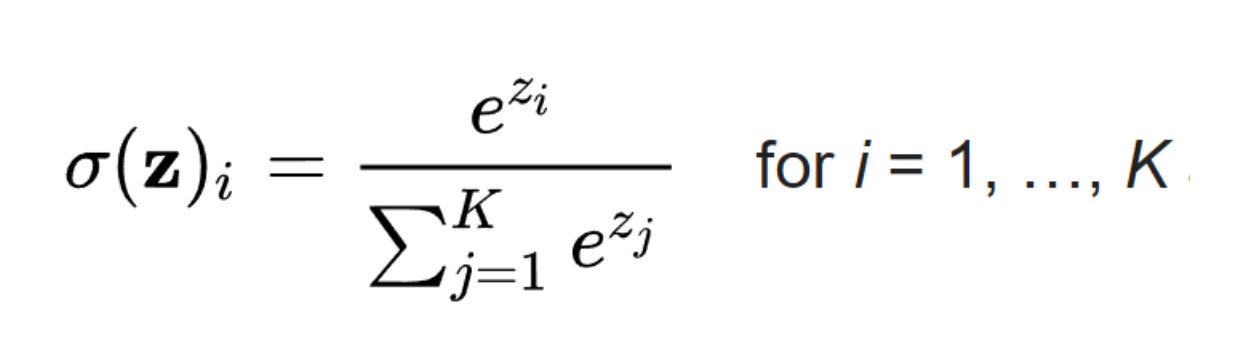

Cost Functions and Gradient Descent
-
Notations
-ŷ: estimation of what the model predicts the label to be
-y: true value
-a: neuron's prediction -
Cost Function
- must be an average so it can output a single value
- Used to keep track of our loss/cost during training to monitor network performance
-
Quadratic cost function
- aL is the prediction at L layer
- Why do we square it?- punish large errors
- keeps everything positive
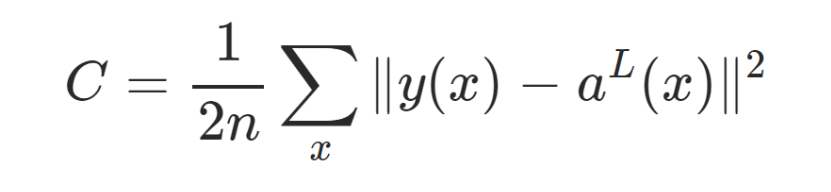
-
Generalization of cost function
-Wis our neural network's weights,Bis our neural network's biases,Sris the input of a single training sample, andEris the desired output of that training sample.
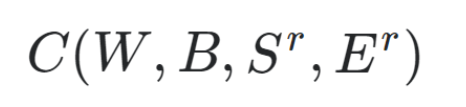
-
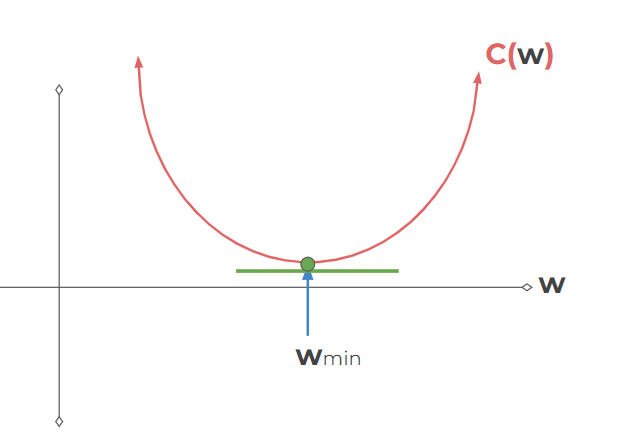
Gradient Descent : find the
wvalues that minimizes the cost
- Learning Rate : how much you should move each time- Larger learning rates result in overshooting but lower computing rate
- Adaptive Gradient Descent : We could adjust the step size in for each step
-
Gradient : derivative for N-dimensional Vectors
∇C(w1,w2,...wn)
-
Cross Entropy Loss Function : for classification problems
- binary classfication :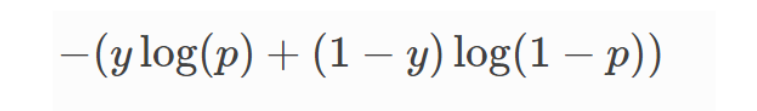
- multi class classification :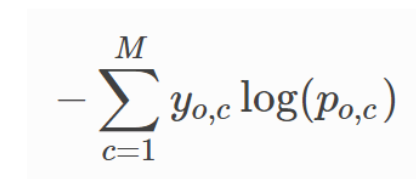
Back Propagation
- Usage of derivatives : find out how sensitive is the cost function to changes in
w
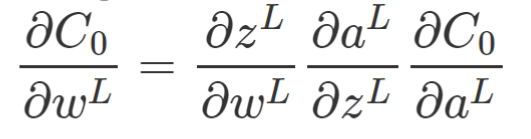
- repeat the same for bias
- Back Propagation Process :
- Step 1 : use inputxto set the activation functionafor the input layer & repeat
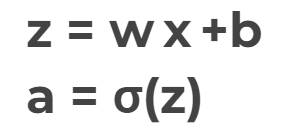
- Step 2 : For each layer, compute
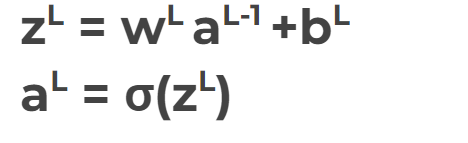
- Step 3 : compute error vector
