#01 ゲームエンジンを支えるゲーム数学_数の構造

我々が最終的に構築するゲーム世界「Vector」は、堅牢なシステムの上に成り立っている。

この「Vector」を正確に理解するためには、「数」が持つシステムや体系についての理解が必要です。

数にはさまざまな種類がありますが、本システムでは

実数集合（The set of real numbers）を使用します。

実数集合とは、数の間に隙間が存在しない連続的な無限の要素で構成された集合です。

---

数の表現方法

「Vector」システムに慣れるためには、数を捉える視点を変える必要があります。
単一の体系に基づいた大小関係で数を並べるのではなく、原点（0）を基準に正負の二つの体系に分け、"大きさ（絶対値）"と"方向（符号）"で数を表現する必要があります。

• 通常の数の並べ方（大小比較）
  例：$-4 < 4$

  

• 原点を中心に、絶対値と方向で表す方法
  例：$-|4| \quad\cdots\quad +|4|$

  

大きさ：$|x|$
方向：正負記号（+ / -）

---

二項演算（Binary Operation）

集合（Set）とは、要素（Element）の集まり（Collection）です。
数の集合が通常の集合と異なる点は、演算が定義されているということです。

---

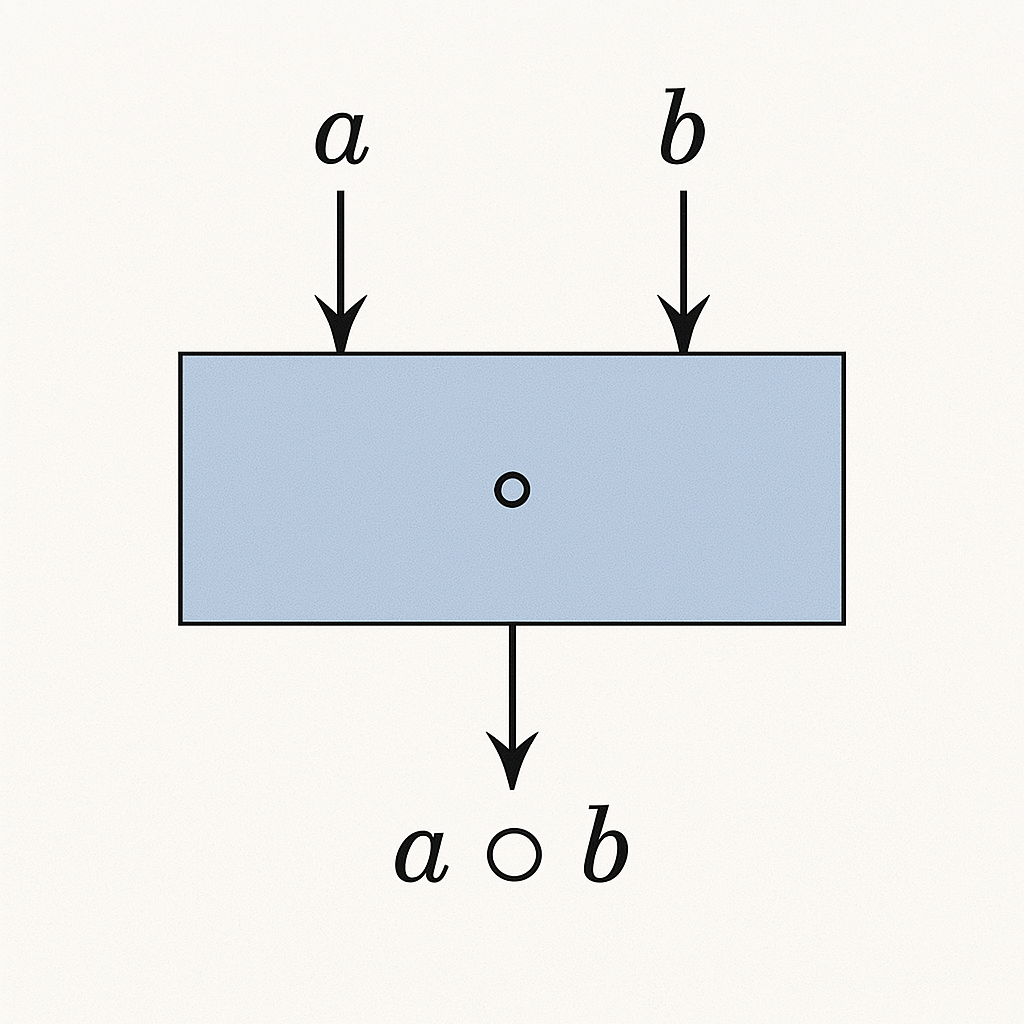
四則演算の再構成

• 減算：$10 - 3 = 10 + (-3)$
• 除算：$10 \div 3 = 10 \cdot \frac{1}{3}$

※ 記号の都合上、掛け算には「×」ではなく「・」を使用することが多い。

---

二項演算の性質

• 交換法則（Commutativity）：$a \cdot b = b \cdot a$
• 結合法則（Associativity）：$(a \cdot b) \cdot c = a \cdot (b \cdot c)$
• 分配法則（Distributivity）：$a \cdot (b + c) = a \cdot b + a \cdot c$

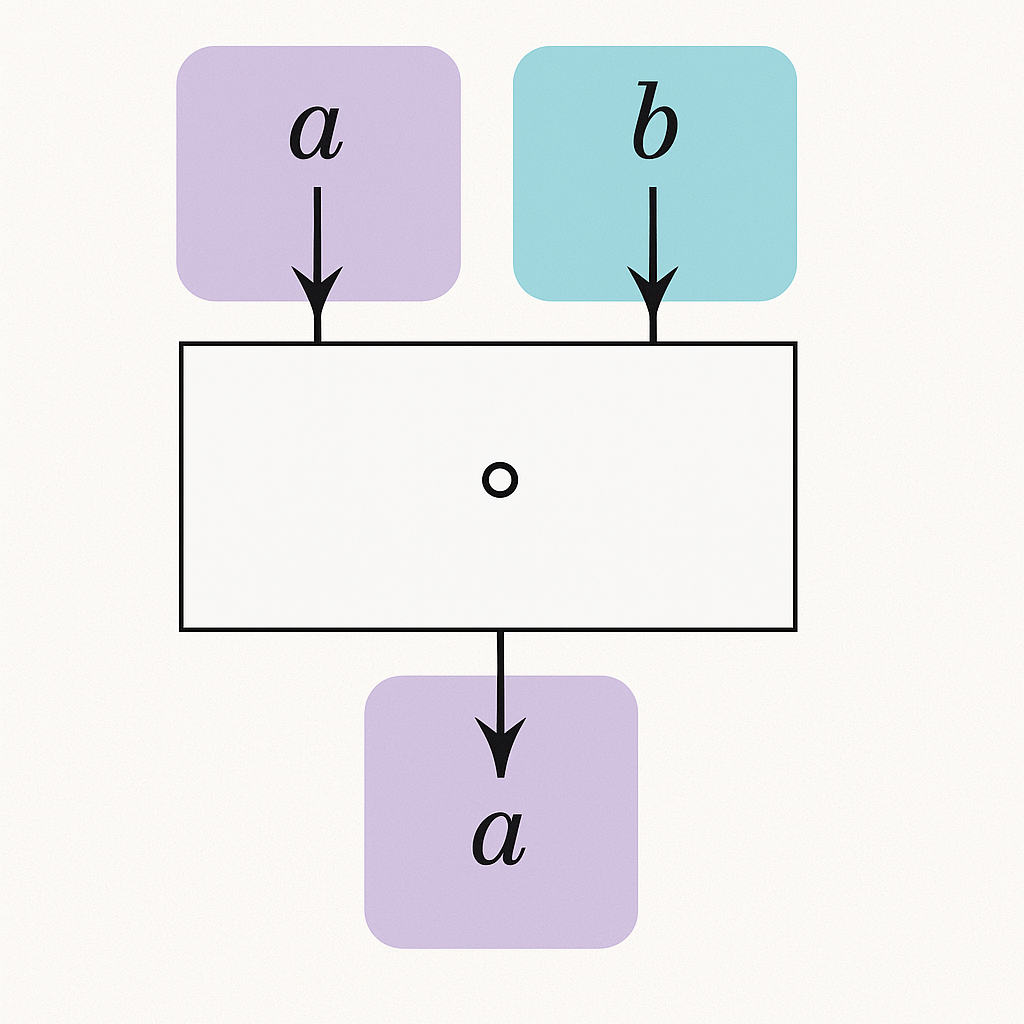
単位元（Identity）

任意の要素 $a$ に対して、演算結果が $a$ 自身となるような特別な要素を単位元と呼びます。

• 加法の単位元：$a + 0 = a$
• 乗法の単位元：$a \cdot 1 = a$

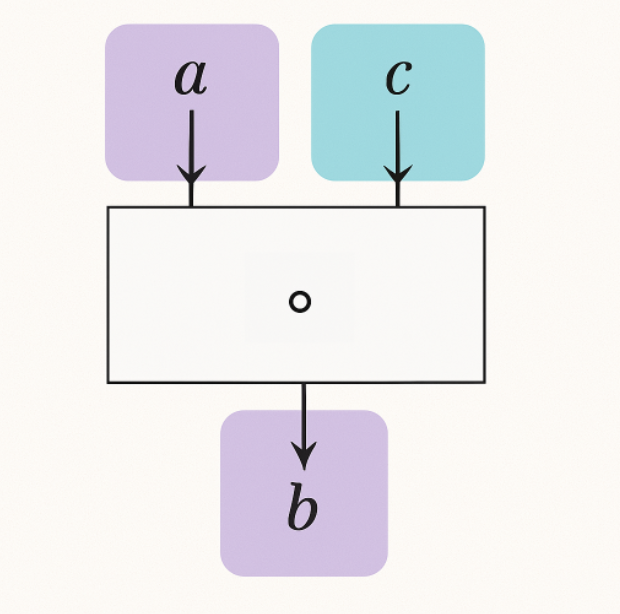
逆元（Inverse）

演算の結果が単位元となるような要素を逆元と呼びます。

• 加法の逆元（反数）：$a + (-a) = 0$
• 乗法の逆元（逆数）：$a \cdot \frac{1}{a} = 1 \quad (a \ne 0)$

引き算は加法の逆元を加える操作と見なせる：$a - b = a + (-b)$
割り算は乗法の逆元を掛ける操作：$a \div b = a \cdot \frac{1}{b}$

---

体（Field）の公理（Axiom）

公理とは、理論体系の中で証明を必要としない基本命題のことです。
これにより、さまざまな数の構造が定義されます。

---

群（Group）の公理

加法に関して以下の公理を満たす数の体系：

1. 加法について閉じている（Closure）
2. 加法は結合法則を満たす（Associativity）
3. 加法の単位元が存在する（Identity）
4. 加法の逆元が存在する（Inverse）

アーベル群（Abelian Group）

加法について交換法則を満たす群

---

環（Ring）の公理

加法・乗法の二つの演算に関して以下の公理を満たす数の体系：

1. 乗法について閉じている（Closure）
2. 乗法は結合法則を満たす（Associativity）
3. 加法と乗法は分配法則を満たす（Distributivity）
4. 乗法の単位元が存在する（Identity）

可換環（Commutative Ring）

乗法において交換法則を満たす環

---

体（Field）の公理（再掲）

体とは、以下を満たす数の構造：

• 0以外のすべての要素に対して乗法の逆元が存在する。
• 加法・乗法共に、交換法則・結合法則・分配法則・単位元・逆元が存在する。

→ 四則演算が自由に適用でき、順序を柔軟に扱える数の体系。
→ 体の構造を持つ数集合には、有理数（$\mathbb{Q}$）、実数（$\mathbb{R}$）、複素数（$\mathbb{C}$）がある。

現実的には多くの場面で実数を用いるが、理論的な体系においては「体の構造を持つ数集合を用いる」と表現することで、明確性と拡張性が高まる。

体集合は通常 $F$ と表記され、その要素をスカラー（Scalar）と呼ぶ。

---

数と演算の抽象化

1. 実数 $a$ と 実数 $b$ を加える
   → 四則演算が使えるが、特定の数体系に限定される

2. スカラー $a$ と スカラー $b$ を加える
   → 体の性質を満たす任意の数体系（$\mathbb{Q}, \mathbb{R}, \mathbb{C}$）で利用可能

→ より汎用的な数と演算のシステムを構築できる

---