#1_週末Study シェーダー・グラフ

With : https://x.com/Creta5164
https://bsky.app/profile/cretapark.me/post/3lnpf32di2k2x

毎日、週末、土曜日、日曜日の 2 時間ずつ
シェーダーグラフを勉強しています。

今日の課題

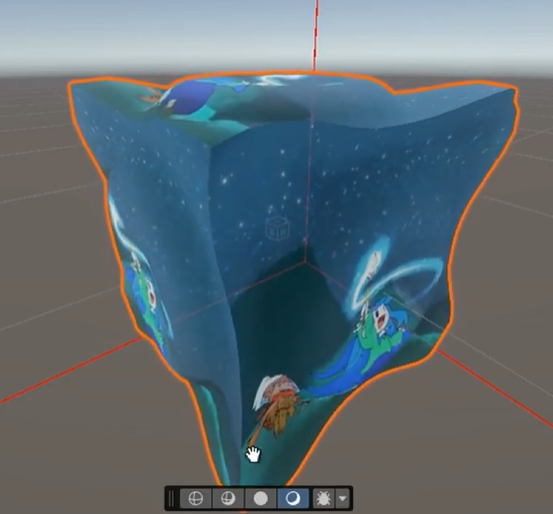
正解

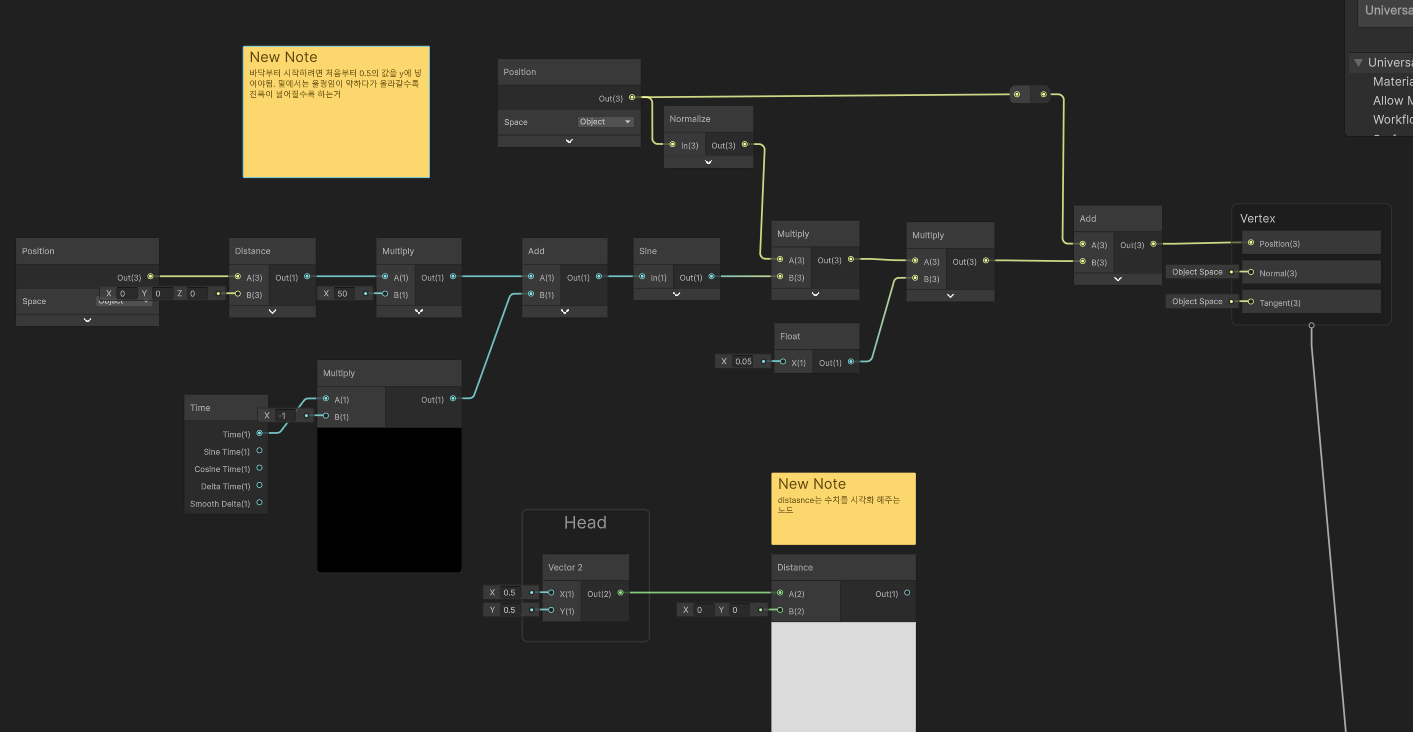
解釈

このグラフがやっていること

• バーテックスの Object Space Position を取得する。
  （＝各頂点の位置情報）

• バーテックスの位置（Position）と (0,0,0) との 距離 (Distance) を計算する。
  → 「中心からの距離」という意味。

• 距離の値に 50 を掛ける。
  → 距離ベースの値を速く大きくするため。（周波数調整のイメージ）

• 現在の 時間 (Time) を取得する。

• 距離 + 時間 を加算した後、Sine 関数 を適用する。
  → 「距離による時間差」を持った Sine 波形を作る。
  → 結果として「中心から波が広がっていく」ような動きになる。

• Sine の値を Normalize 方向 に掛ける。
  → バーテックスをノーマル方向（通常は上方向）に押し出す。
  → メッシュがドーナツ状に膨らむように動く。

• この移動量に 0.05 を掛けて、揺れの大きさを抑える。
  → 動きが大きすぎないようにスケール調整。

• 最後に、元の位置（Position）に動きを加算して、
  最終的な新しいバーテックス位置を作る。

要点まとめ

「中心(0,0,0)からの距離に応じて時間差のあるSine波を生成し、
バーテックスをノーマル方向に押し出すウェーブシェーダー」

Distance を使う理由

• 距離 (Distance) によって Sine 波の進み具合や位相が変わるため。
• その結果、「波が中心から広がっていく」ような表現ができる。

図を見て理解したフローを一言でまとめると

「中心点基準で距離別のSine波を作り、ノーマル方向にバーテックスを押し出す構成」