네트워크 유량 : 알고리즘 노트

Drakk·2021년 7월 26일

C mcmf 네트워크유량 알고리즘 알고리즘노트 이분매칭 최대유량

알고리즘노트

목록 보기

2/5

🔪소개및 개요

🔴임시공지

본 포스팅은 미완성 포스팅입니다.
계속 만들어지는 중입니다.
예상 완성일은 2021-08-06입니다.

🔴 미완성요소 🔴
🔴 MCMF
🔴 네트워크유량이 사용된 알고리즘 문제들 예제
🔴 추가설명
🔴 이분매칭

💎개요

본 포스팅에서는 알고리즘 문제풀이에서 사용하는 몇가지 네트워크유량과 관련된 기본적인 요소들을 종류별로 작성할것입니다.
이 글은 어디까지나 저의 개인적인 노트, 정리같은것이기 때문에 이론들을 깊게 설명하는것은 하지 않겠습니다.

소스코드는 c++ , c# 사용하겠습니다.

💎참고

안경잡이 개발자
알고리즘 문제해결전략

💎개발환경

2021-07-27기준 Windows10 Home 사용했으며, 컴파일러는 MSVC, GCC를 사용했습니다.
c++버전은 17사용했습니다.
c#버전은 .Net6.0이랑 .Net4.72사용했습니다.

🔪네트워크 유량

💎포드-풀커슨

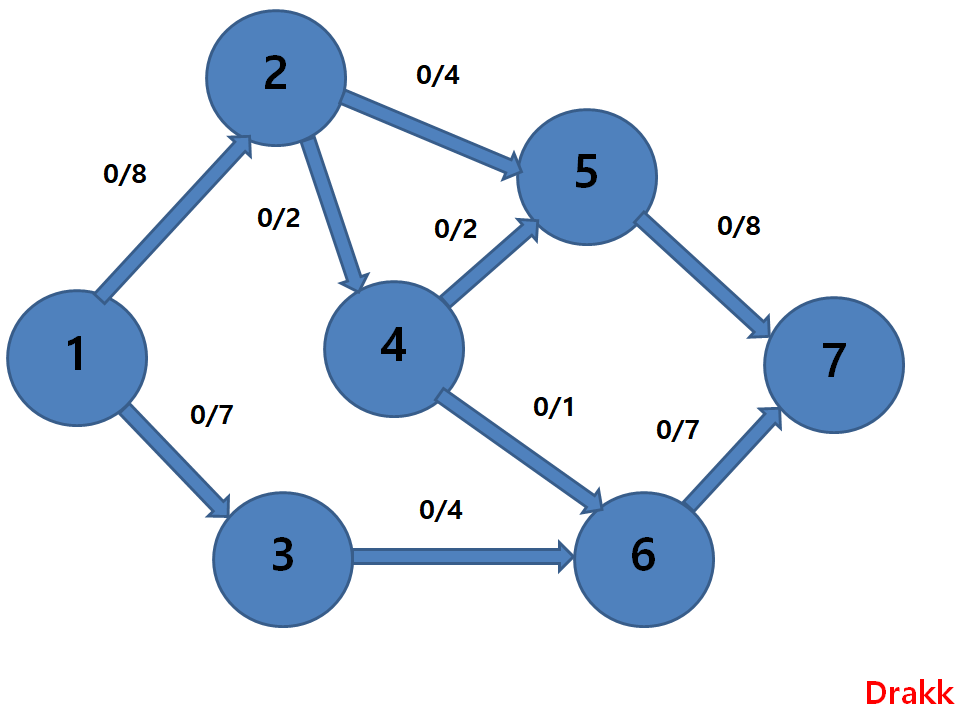
포드-풀커슨 알고리즘은 네트워크 유량을 해결하는데 사용되는 가장 기본적인 알고리즘입니다.

C++

#include <bits/stdc++.h>

constexpr int MAX = 7 + 1;
constexpr int INF = 987654321;

std::vector<int> adj[MAX];
int c[MAX][MAX], f[MAX][MAX];

void makeGraph(int a, int b, int cost) {
	adj[a].push_back(b);
	adj[b].push_back(a);
	c[a][b] = cost;
	c[b][a] = 0;
}

int FordFulkerson(int start, int end) {
	int result = 0;

	while (true) {
		std::vector<int> dist(MAX, -1);
		std::queue<int> q;
		q.push(start);

		while (!q.empty()) {
			int current = q.front();
			q.pop();

			for (int i = 0; i < adj[current].size(); ++i) {
				int next = adj[current][i];

				if (c[current][next] - f[current][next] > 0 && dist[next] == -1) {
					dist[next] = current;
					q.push(next);
					if (next == end)
						break;
				}
			}
		}

		if (dist[end] == -1)
			break;

		int flow = INF;
		for (int i = end; i != start; i = dist[i])
			flow = std::min(flow, c[dist[i]][i] - f[dist[i]][i]);

		for (int i = end; i != start; i = dist[i]) {
			f[dist[i]][i] += flow;
			f[i][dist[i]] -= flow;
		}

		result += flow;
	}

	return result;
}

int main() {
	makeGraph(1, 2, 8);
	makeGraph(1, 3, 7);
	makeGraph(2, 4, 2);
	makeGraph(3, 6, 4);
	makeGraph(2, 5, 4);
	makeGraph(4, 5, 2);
	makeGraph(4, 6, 1);
	makeGraph(5, 7, 8);
	makeGraph(6, 7, 7);

	std::cout << FordFulkerson(1, 7);
}

C#

using System;
using System.Collections.Generic;

namespace NetworkFlow
{
    class Program
    {
        private const int MAX = 7 + 1;
        private const int INF = 987654321;

        static private List<List<int>> adj = new List<List<int>>();
        private static int[,] c = new int[MAX, MAX];
        private static int[,] f = new int[MAX, MAX];

        static private void makeGraph(int a, int b, int cost)
        {
            adj[a].Add(b);
            adj[b].Add(a);
            c[a, b] = cost;
            c[b, a] = 0;
        }

        static private int FordFulkerson(int start, int end)
        {
            int result = 0;

            while (true)
            {
                List<int> dist = new List<int>();
                for (int i = 0; i < MAX; ++i) dist.Add(-1);
                Queue<int> q = new Queue<int>();
                q.Enqueue(start);

                while(q.Count > 0)
                {
                    int current = q.Dequeue();

                    for(int i = 0; i < adj[current].Count; ++i)
                    {
                        int next = adj[current][i];

                        if(c[current, next] - f[current, next] > 0 && dist[next] == -1)
                        {
                            dist[next] = current;
                            q.Enqueue(next);
                            if (next == end)
                                break;
                        }
                    }
                }

                if (dist[end] == -1)
                    break;

                int flow = INF;
                for (int i = end; i != start; i = dist[i])
                    flow = Min(flow, c[dist[i], i] - f[dist[i], i]);

                for (int i = end; i != start; i = dist[i])
                {
                    f[dist[i], i] += flow;
                    f[i, dist[i]] -= flow;
                }

                result += flow;
            }

            return result;
        }

        static private int Min(int a, int b)
        {
            return a < b ? a : b;
        }


        static void Main(string[] args)
        {
            for (int i = 0; i < MAX; ++i)
                adj.Add(new List<int>());
            
            makeGraph(1, 2, 8);
            makeGraph(1, 3, 7);
            makeGraph(2, 4, 2);
            makeGraph(3, 6, 4);
            makeGraph(2, 5, 4);
            makeGraph(4, 5, 2);
            makeGraph(4, 6, 1);
            makeGraph(5, 7, 8);
            makeGraph(6, 7, 7);

            Console.WriteLine(FordFulkerson(1, 7));
        }
    }
}

💎in-out 분할정점 최대유량

in-out 분할정점 최대유량은 한 정점 안에서 두개의 정점으로 분할되는 정점을 말합니다. 이러한 정점들의 최대유량을 포드풀커슨알고리즘과 결합합니다.

C++

#include <bits/stdc++.h>

constexpr int N = 7;
constexpr int MAX = (N + 1) * 2;
constexpr int OUT = (N + 1);

constexpr int INF = 987654321;

std::vector<int> adj[MAX];
int c[MAX][MAX], f[MAX][MAX];

void makeGraph(int a, int b, int cost) {
	adj[a + OUT].push_back(b);
	adj[b].push_back(a + OUT);
	c[a + OUT][b] = cost;
	c[b][a + OUT] = 0;

	adj[b + OUT].push_back(a);
	adj[a].push_back(b + OUT);
	c[b + OUT][a] = cost;
	c[a][b + OUT] = 0;
}

int FordFulkerson(int start, int end) {
	int result = 0;

	while (true) {
		std::vector<int> dist(MAX, -1);
		std::queue<int> q;
		q.push(start);

		while (!q.empty()) {
			int current = q.front();
			q.pop();

			for (int i = 0; i < adj[current].size(); ++i) {
				int next = adj[current][i];

				if (c[current][next] - f[current][next] > 0 && dist[next] == -1) {
					dist[next] = current;
					q.push(next);
					if (next == end)
						break;
				}
			}
		}

		if (dist[end] == -1)
			break;

		int flow = INF;
		for (int i = end; i != start; i = dist[i])
			flow = std::min(flow, c[dist[i]][i] - f[dist[i]][i]);

		for (int i = end; i != start; i = dist[i]) {
			f[dist[i]][i] += flow;
			f[i][dist[i]] -= flow;
		}

		result += flow;
	}

	return result;
}

int main() {
	for (int i = 1; i <= N; ++i) {
		adj[i].push_back(i + OUT);
		adj[i + OUT].push_back(i);
		c[i][i + OUT] = 1;
		c[i + OUT][i] = 0;
	}

	makeGraph(1, 2, 8);
	makeGraph(1, 3, 7);
	makeGraph(2, 4, 2);
	makeGraph(3, 6, 4);
	makeGraph(2, 5, 4);
	makeGraph(4, 5, 2);
	makeGraph(4, 6, 1);
	makeGraph(5, 7, 8);
	makeGraph(6, 7, 7);

	std::cout << FordFulkerson(1 + OUT, 7);
}

이번에 C#은 WinForm Framework로 해봤습니다.
설정화면은 이렇습니다.
"ClickMe!"라는 라벨을 누르면 최대유량이 나오게끔 했습니다.

C#

using System;
using System.Collections.Generic;
using System.Windows.Forms;

namespace inOut
{
    public partial class Form1 : Form
    {
        private const int N = 7;
        private const int MAX = (N + 1) * 2;
        private const int OUT = N + 1;
        private const int INF = 987654321;

        static private List<List<int>> adj = new List<List<int>>();
        private static int[,] c = new int[MAX, MAX];
        private static int[,] f = new int[MAX, MAX];

        static private void makeGraph(int a, int b, int cost)
        {
            adj[a + OUT].Add(b);
            adj[b].Add(a + OUT);
            c[a + OUT, b] = cost;
            c[b, a + OUT] = 0;

            adj[b + OUT].Add(a);
            adj[a].Add(b + OUT);
            c[b + OUT, a] = cost;
            c[a, b + OUT] = 0;
        }

        static private int FordFulkerson(int start, int end)
        {
            int result = 0;

            while (true)
            {
                List<int> dist = new List<int>();
                for (int i = 0; i < MAX; ++i) dist.Add(-1);
                Queue<int> q = new Queue<int>();
                q.Enqueue(start);

                while (q.Count > 0)
                {
                    int current = q.Dequeue();

                    for (int i = 0; i < adj[current].Count; ++i)
                    {
                        int next = adj[current][i];

                        if (c[current, next] - f[current, next] > 0 && dist[next] == -1)
                        {
                            dist[next] = current;
                            q.Enqueue(next);
                            if (next == end)
                                break;
                        }
                    }
                }

                if (dist[end] == -1)
                    break;

                int flow = INF;
                for (int i = end; i != start; i = dist[i])
                    flow = Min(flow, c[dist[i], i] - f[dist[i], i]);

                for (int i = end; i != start; i = dist[i])
                {
                    f[dist[i], i] += flow;
                    f[i, dist[i]] -= flow;
                }

                result += flow;
            }

            return result;
        }

        static private int Min(int a, int b)
        {
            return a < b ? a : b;
        }


        static private void Init()
        {
            for (int i = 0; i < MAX; ++i)
                adj.Add(new List<int>());

            for(int i = 1; i <= N; ++i)
            {
                adj[i].Add(i + OUT);
                adj[i + OUT].Add(i);
                c[i, i + OUT] = 1;
                c[i + OUT, i] = 0;
            }

            makeGraph(1, 2, 8);
            makeGraph(1, 3, 7);
            makeGraph(2, 4, 2);
            makeGraph(3, 6, 4);
            makeGraph(2, 5, 4);
            makeGraph(4, 5, 2);
            makeGraph(4, 6, 1);
            makeGraph(5, 7, 8);
            makeGraph(6, 7, 7);
        }

        public Form1()
        {
            InitializeComponent();
        }

        private void Form1_Load(object sender, EventArgs e)
        {
            Init();
        }

        private void label1_Click(object sender, EventArgs e)
        {
            label1.Text = FordFulkerson(1 + OUT, 7).ToString();
        }
    }
}

💎최소비용 최대유량 (MCMF)

미완성(현재 만드는중입니다!)

C++

C#

💎이분매칭

이분매칭은 어떠한 정점과 다른정점을 일련의 순서에 맞게 매치시키는 알고리즘입니다.

C++

#include <bits/stdc++.h>

constexpr int MAX = 4;
constexpr int INF = 987654321;

std::vector<int> adj[MAX + 1];
int dist[MAX + 1];
bool visit[MAX + 1];

bool dfs(int start) {
	for (int i = 0; i < adj[start].size(); ++i) {
		int next = adj[start][i];

		if (visit[next])
			continue;
		visit[next] = true;

		if (dist[next] == 0 || dfs(dist[next])) {
			dist[next] = start;
			return true;
		}
	}
	return false;
}

int BipartiteMatching() {
	int result = 0;

	for (int i = 1; i <= MAX; ++i) {
		std::fill(visit, visit + MAX + 1, false);
		if (dfs(i))
			++result;
	}

	return result;
}

int main() {
	adj[1].push_back(1);
	adj[1].push_back(2);
	adj[2].push_back(1);
	adj[3].push_back(4);
	adj[4].push_back(3);

	int result = BipartiteMatching();
	std::cout << result << '\n';

	for (int i = 1; i <= MAX; ++i) {
		if (dist[i] != 0)
			std::cout << dist[i] << " =>> " << i << '\n';
	}
}