최소비용 경로탐색 : 알고리즘 노트

Drakk·2021년 8월 3일
C경로탐색벨만포드알고리즘알고리즘노트최소비용최소비용 경로탐색
0

알고리즘노트

목록 보기
3/5
post-thumbnail

🔪소개및 개요

💎개요

본 포스팅에서는 벨만포드 알고리즘을 이용한 최소비용 경로탐색 알고리즘에 관한 개인적인 정리에 대한 내용을 담고있습니다.
이 글은 어디까지나 저의 개인적인 노트, 정리같은내용이기 때문에 이론들을 깊게 설명하는것은 하지 않겠습니다.

프로그래밍언어는 c++ , c# 사용하겠습니다.

💎참고

CP_ALGORITHMS

💎개발환경

2021-08-04기준 Windows10 Home 사용했으며, 컴파일러는 MSVC, GCC를 사용했습니다.
c++버전은 17사용했습니다.
c#버전은 .Net6.0이랑 .Net4.72사용했습니다.

🔪벨만-포드 알고리즘

💎정리노트

벨만-포드 알고리즘은 어떠한 그래프가 있을때, 시작지점에서 도착지점까지 이르는데 필요한 최소비용을 구하는 알고리즘입니다.

*V: 간선의 개수
우선 이번에 만들어볼 알고리즘의 전체적인 시간복잡도는 O(M + N) + O(VE)입니다.

minV함수와 출력부분을 제외하고, 순수 알고리즘 부분은 O(VE)입니다.

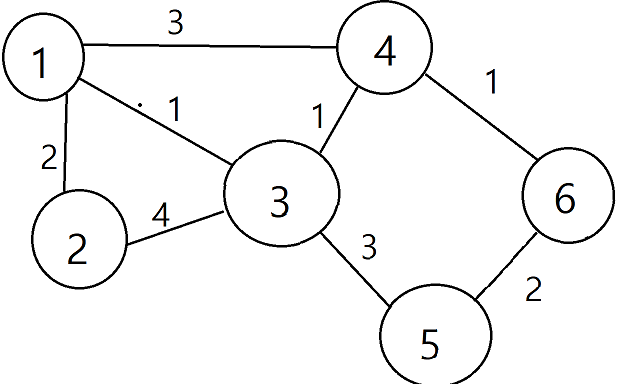
아래사진은 이번내용의 알고리즘을 적용해볼 예시용 그래프입니다.
참고로 단방향그래프입니다, 화살표를 그리는것을 까먹었습니다.
하지만 다 작은정점에서 큰정점으로 가는 방향입니다.



💎소스코드

C++17 (소스코드가 길어보이는것은 착시입니다. 주석때문입니다.)

#include <bits/stdc++.h>

// INF: 무한대수정의
constexpr int INF = 987654321;

// a: 현재지점, b: 다음지점, cost: 거리에 대한 비용
struct edge
{
	int a, b, cost;
};

// e: 연결된 간선과 비용을 저장하는 배열
std::vector<edge> e;

// n: 정점의 개수, m: 간선의 개수, v: 출발점, t: 도착점 
int n, m, v, t;

// minV: 만약 출발점이 0이 아닐경우에 대비하여 만든 함수
// *만약 출발점이 1이고, 도착점이 6인데 n이 6이면 오버플로우 발생하기때문이다.
// *위의 예시에 대한 경우를 안정화시키기 위한 함수
int minV() {
	int result = INF;
	for (std::size_t i = 0; i < e.size(); ++i) {
		result = std::min(result, std::min(e[i].a, e[i].b));
	}

	result = std::max(v, result);
	return result;
}

void BellmanFord()
{
	// 이 부분은 굳이 안넣어주셔도됩니다.
    	// 넣어준이유는 출발점이 0이아닐경우에 대비해서 넣은겁니다.
	n += minV();

	// visit: 방문여부확인 & 해당 정점에대한 비용저장용 변수
	std::vector<int> visit(n, INF);
    
    	// 시작지점은 이동비용이 0입니다.
	visit[v] = 0;
    
    	// p: 경로탐색에 필요한 경로저장용 배열
	std::vector<int> p(n, -1);

	// 이 부분은 평범한 벨만-포드 알고리즘 구현부분입니다.
    	// 모르시는 분들은 그래프이론공부하고 오시는것을 추천드립니다.
	while (true)
	{
		bool flag = false;
		for (int j = 0; j < m; ++j)
			if (visit[e[j].a] < INF)
				if (visit[e[j].b] > visit[e[j].a] + e[j].cost)
				{
					visit[e[j].b] = visit[e[j].a] + e[j].cost;
					p[e[j].b] = e[j].a;
					flag = true;
				}
		if (!flag)  break;
	}

	// 조건분기[TRUE]: 도착지점까지 갈수없는 그래프
	if (visit[t] == INF)
		std::cout << "이 그래프에서 최소비용경로는 존재하지 않습니다.";
        
        // 조건분기[FALSE]: 도착지점까지 갈수있는 그래프
	else
	{
    		// path: 최소비용에 대한 탐색된 경로가 저장된 배열
		std::vector<int> path;
        
        	// -1이 나올때까지 거꾸로 순회하면서 그때의 정점을 push한다.
		for (int cur = t; cur != -1; cur = p[cur])
			path.push_back(cur);
		std::reverse(path.begin(), path.end());

		std::cout << "최소비용은 " << visit[t] << "입니다." << '\n';
		std::cout << v << "에서 " << t << "까지의 최소비용경로: ";
		for (std::size_t i = 0; i < path.size(); ++i)
			std::cout << path[i] << ' ';
	}
}

// makeGraph: 간선만드는 함수
void makeGraph(int start, int end, int cost) {
	e.push_back({ start, end, cost });
}

int main() {
	n = 6; //정점의 개수 
	m = 8; //간선의 개수 
	v = 1; //출발점 
	t = 6; //도착점 

	makeGraph(1, 2, 2);
	makeGraph(1, 4, 3);
	makeGraph(1, 3, 1);
	makeGraph(2, 3, 4);
	makeGraph(3, 4, 1);
	makeGraph(3, 5, 3);
	makeGraph(4, 6, 1);
	makeGraph(5, 6, 2);

	BellmanFord();
}



C#은 Winform .netframework로 했습니다.
뭔가 시각적으로 보이니까 더 재밌어요!!ㅠㅠㅋㅋ

C# (.Net 6.0)

using System;
using System.Collections.Generic;
using System.Linq;
using System.Windows.Forms;

namespace ShortestPath
{
    public partial class Form1 : Form
    {
        struct Edge
        {
            public int a, b, cost;

            public Edge(int a, int b, int cost)
            {
                this.a = a;
                this.b = b;
                this.cost = cost;
            }
        }

        struct ReturnType
        {
            public List<int> Path;
            public int Cost;
        }

        private static List<Edge> edges = new List<Edge>();
        private static int N, M;


        private static int Min(int a, int b)
        {
            return (a < b) ? a : b;
        }

        private static int Max(int a, int b)
        {
            return (a > b) ? a : b;
        }

        private static int MaxVertax()
        {
            int result = 0;

            for(int i = 0; i < edges.Count; ++i)
            {
                result = Max(result, Max(edges[i].a, edges[i].b));
            }

            return result;
        }

        private static int MinVertax(int s)
        {
            int result = 987654321;

            for (int i = 0; i < edges.Count; ++i)
            {
                result = Min(result, Min(edges[i].a, edges[i].b));
            }

            result = Max(result, s);

            return result;
        }

        private static ReturnType Bellman_ford(int start, int end)
        {
            M = edges.Count;

            N = MaxVertax();
            N += MinVertax(start);

            ReturnType rType = new ReturnType();
            List<int> visit = new List<int>();
            List<int> p = new List<int>();
            for (int i = 0; i < N; ++i)
            {
                visit.Add(987654321);
                p.Add(-1);
            }

            visit[start] = 0;

            while (true)
            {
                bool flag = false;
                for(int i = 0; i < M; ++i)
                {
                    if (visit[edges[i].a] < 987654321)
                    {
                        if (visit[edges[i].b] > visit[edges[i].a] + edges[i].cost)
                        {
                            visit[edges[i].b] = visit[edges[i].a] + edges[i].cost;
                            p[edges[i].b] = edges[i].a;
                            flag = true;
                        }
                    }
                }
                if (!flag) break;
            }

            List<int> Path = new List<int>();
            if (visit[end] != 987654321) {
                for (int i = end; i != -1; i = p[i])
                {
                    Path.Add(i);
                }
                Path.Reverse();
            }

            rType.Cost = visit[end];
            rType.Path = Path;
            return rType;
        }

        public Form1()
        {
            InitializeComponent();
        }

        private void Form1_Load(object sender, EventArgs e)
        {
            textBox4.ReadOnly = true;
            textBox5.ReadOnly = true;
        }

        private void button1_Click(object sender, EventArgs e)
        {
            edges.Add(new Edge(
                Convert.ToInt32(textBox1.Text),
                Convert.ToInt32(textBox2.Text),
                Convert.ToInt32(textBox3.Text)));

            textBox1.Text = "";
            textBox2.Text = "";
            textBox3.Text = "";
        }

        private void button2_Click(object sender, EventArgs e)
        {
            var result = Bellman_ford(Convert.ToInt32(textBox6.Text), Convert.ToInt32(textBox7.Text));
            if (result.Path.Count != 0)
            {
                string str = "";
                var arr = result.Path.ToArray<int>();

                for (int i=0;i<arr.Length;++i)
                {
                    str = str + arr[i].ToString();
                    if (i != arr.Length - 1) str += " -> ";
                }

                textBox5.Text = str;
                textBox4.Text = result.Cost.ToString();
            }
        }

        private void button3_Click(object sender, EventArgs e)
        {
            edges.Clear();
            textBox1.Text = "";
            textBox2.Text = "";
            textBox3.Text = "";
            textBox4.Text = "";
            textBox5.Text = "";
            textBox6.Text = "";
            textBox7.Text = "";
        }

        private void textBox1_TextChanged(object sender, EventArgs e) { } // A
        private void textBox2_TextChanged(object sender, EventArgs e) { } // B
        private void textBox3_TextChanged(object sender, EventArgs e) { } // Cost
        private void textBox4_TextChanged(object sender, EventArgs e) { } // 최소비용
        private void textBox5_TextChanged(object sender, EventArgs e) { } // 최소비용 경로
        private void textBox6_TextChanged(object sender, EventArgs e) { } // Start
        private void textBox7_TextChanged(object sender, EventArgs e) { } // End
    }
}



💎프로그램 실행

C++17

사실 이것말고 개인적으로 다익스트라 알고리즘에도 아래 코드와같이 똑같은 테크닉을 사용했는데 정상적으로 작동했습니다. 신기!!방기!!하네요~

똑같은 테크닉을 다익스트라에다가도 적용시켜본 C++17소스코드

#include <bits/stdc++.h>

constexpr int MAX = 101;
constexpr int INF = 987654321;

std::vector<std::pair<int, int>> adj[MAX];
int cost[MAX];

void dijkstra(int start){
	std::vector<int> p(MAX, -1);
	std::priority_queue<std::pair<int, int>, std::vector<std::pair<int, int>>, std::greater<std::pair<int, int>>> pq;
	cost[start] = 0;
	pq.push({ start, 0 });
	
	while(!pq.empty()){
		int current = pq.top().first;
		int dist = pq.top().second;
		pq.pop();
		
		if(cost[current] < dist) continue;
		for(std::size_t i=0;i<adj[current].size();++i){
			int next = adj[current][i].first;
			int ndist = dist + adj[current][i].second;
			
			if(ndist < cost[next]){
				cost[next] = ndist;
				p[next] = current;
				pq.push({ next, ndist });
			}
		}
	}
	
	std::vector<int> path;
	for(int i=5;i!=-1;i=p[i]){
		path.push_back(i);
	}
	std::reverse(path.begin(), path.end());
	
	for(auto const& i : path){
		std::cout << i << ' ';
	}
	std::cout << "\n\n";
}

void makeGraph1(int s, int e, int c){
	adj[s].push_back({ e, c });
}

void makeGraph2(int s, int e, int c, int rc){
	adj[s].push_back({ e, c });
	adj[e].push_back({ s, rc });
}

int main(){
	int n = 5;
	
	makeGraph1(0, 1, 2);
	makeGraph1(0, 2, 4);
	makeGraph1(1, 2, 5);
	makeGraph1(1, 4, 3);
	makeGraph1(0, 3, 6);
	makeGraph2(3, 5, 3, 3);
	makeGraph2(2, 4, 2, 3);
	makeGraph2(2, 3, 2, 1);
	makeGraph2(4, 5, 5, 1);
	
	for(int i=0;i<=n;++i) cost[i] = INF;
	dijkstra(0);
	
	for(int i=0;i<=n;++i){
		std::cout << cost[i] << ' ';
	}
}


첫번째줄이 0에서 5까지가는데 드는 최소비용 경로이고,
그다음줄은 0부터 5까지의 정점에 대한 각각의 최소비용입니다.

C# (.Net 6.0)



💎다운로드

C# winform은 만들기 귀찮으실것같아서 저가 만들던거 공유하겠습니다.
C# winform 샘플 다운로드
비번은 "naw6"입니다.



🔴마치며...

벨만-포드 알고리즘은 최소비용을 구하는데 사용하는 알고리즘으로써,
비슷한 최소비용 알고리즘으로는 다익스트라, 플로이드-와샬 알고리즘이 존재합니다.

개인적으로 최소비용을 구하는데에만 연습했었는데, 이번 계기로 최소비용에 대한 경로탐색을 하는 테크닉에 대해서도 공부하게되었습니다.

개인적으로 되게 도움이 많이 되었던 공부였습니다.

profile
Drakk
C++ / Assembly / Python 언어를 다루고 있습니다!
이전 포스트

네트워크 유량 : 알고리즘 노트

다음 포스트

a* 길찾기 알고리즘 : C++

0개의 댓글