✅혼자 공부하는 머신러닝+딥러닝
진도: Chapter 03
keyword : 지도학습 알고리즘 > 회귀 regression >
[k-최근접이웃 회귀 / (선형회귀 / 다항회귀 / 다중회귀) / (릿지회귀, 라쏘회귀)] > 예측 predict
사용 sklearn 패키지 :
1. neighbors (KNeighborsRegressor),
2. model_selection (train_test_split),
3. metrics (mean_absolute_error),
4. linear_model(=추정기estimator)(LinearRegression),
5. preprocessing(=변환기transformer)
: fit 특성조합찾기(train만 input!!)
: transform 특성변환(train, test input)
(PolynomialFeatures다중회귀)(StandardScaler정규화)
실습파일 : Perch.ipynb

(완료) 기본 미션 : Ch.03(03-1) 2번 문제 출력 그래프 인증하기
=>이웃 개수인 n이 커질 수록 모델이 단순해진다!!!

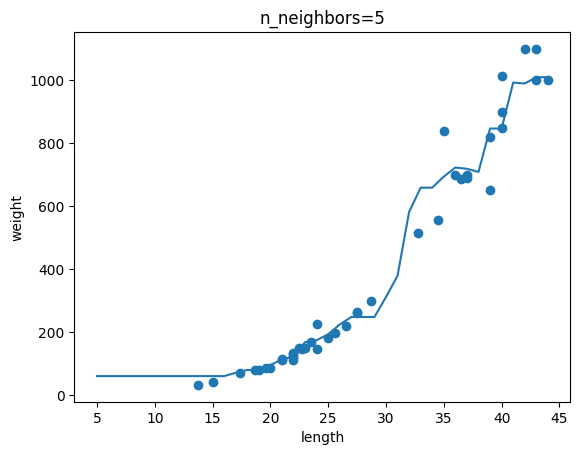
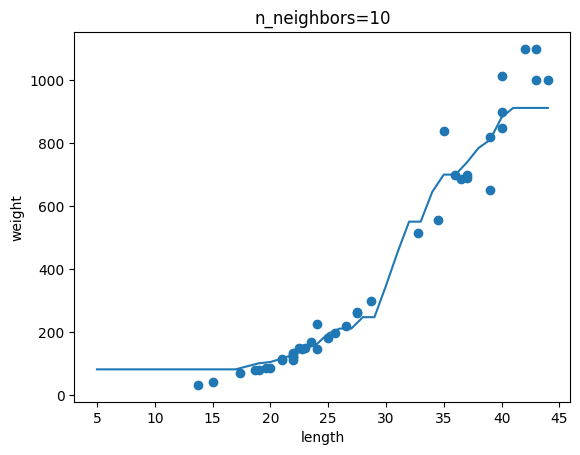
(완료) 선택 미션 : 모델 파라미터에 대해 설명하기
*모델 파라미터 model parameter
: 가중치와 보정치를 머신러닝 알고리즘이 모델에서 찾은 값(특성에서 학습한 파라미터)이다.
머신러닝 알고리즘의 훈련 과정은 최적의 모델 파라미터를 찾는 것이다. 이를 모델 기반 학습이라고 부른다.*k-최근접 이웃의 경우 모델 파라미터가 없는 사례 기반 학습이다.
회귀 알고리즘의 유래 : 19세기 Francis Galton이 부모와 아이의 키 상관관계를 비교하던 중, 아이가 부모보다 크지 않은 사실을 관찰하고 '평균으로의 회귀' 를 알았다.
이후, 두 변수 사이의 상관관계를 분석하는 방법을 회귀라 일컫는다.
✅03-1 : k-최근접 이웃 회귀
[k-최근접 이웃 회귀모델 만들기]
예측하려는 샘플에 가장 가까운 k개의 이웃 지정.
이웃한 샘플의 타깃값을 평균하면, 샘플의 예측 타깃값 알 수 있다.
- 1) 데이터 준비
- 2) 데이터 가공 : array.reshape(행,열)
# sklearn의 훈련 세트는 2차원 배열이어야 한다.
ex) train_input의 크기가 (42, )인 1차원 배열일 때, 2차원 배열 (42,1)로 바꾸는 법
-> train_input.reshape(42,1)
-> train_input.reshape(-1,1) #크기에 -1을 지정하면 나머지 원소개수로 채우라는 뜻.-
3) 훈련 세트 분리 : train_test_split()
-
4) 알고리즘 : 회귀모델 (R^2값 반환)
from sklearn.neighbors import KNeighborsRegressor
knr = KNeighborsRegressor() -
5) 모델 훈련 : knr.fit(train_input, train_target)
-
6) 모델 평가 : knr.score(test_input, test_target)
-> (임의의 예측값, 임의의 타깃) 으로 회귀
-> 결정계수 출력 #0.992809406101064
# 결정계수 coefficient of determination (=R^2)
R^2 = 1 - (target-predict)^2 의 합 / (target-mean)^2 의 합
: target의 평균정도를 예측 시(분자가 분모와 비슷) = 0에 가까운 값
: target에 가깝게 예측 시(분자가 0에 가까움) = 1에 가까운 값
# 예측의 오차값 구하기
-> target과 predict 값 사이의 차이를 구하기.
-> mean_absolute_error : 타깃, 예측의 오차의 절댓값을 평균하여 반환
from sklearn.metrics import mean_absolute_error
# 테스트 세트에 대한 예측을 만들기
test_prediction = knr.predict(test_input)
#테스트 세트에 대한 평균 절댓값 오차를 계산
mae = mean_absolute_error(test_target, test_prediction)
print(mae)
>19.157142857142862 : 결과에서 예측이 평균 19g정도 타깃값과 다름scikit-learn은 회귀 모델의 점수로 R^2(결정계수) 값을 반환한다.
이 값은 1에 가까울 수록 좋다.
정량적인 평가를 하려면 절댓값 오차 등 사용 가능하다.
(from sklearn.metrics import mean_absolute_error)
과대적합 vs 과소적합
-과대적합 overfitting : 훈련세트점수 좋음, 테스트세트점수 나쁨 (실전에 부적합, 새로운 샘플에 대해 예측 힘듦)
-과소적합 underfitting : 훈련세트점수 나쁨, 테스트세트점수 좋음 or 둘다 점수 나쁨 (학습이 덜 됨, 모델이 너무 단순)
-> 이웃의 개수를 줄이면 국지적 패턴에 민감해짐 = 모델 복잡해짐
k-최근접 이웃의 문제점
최근접 이웃값으로 샘플을 지정하기 때문에, 새로운 샘플이 훈련 세트의 범위를 벗어나면 예측이 힘들어진다.
ex) 값이 아무리 증가해도, 일정 값 초과라면 같은 결과만 예측.
-> 머신러닝 모델은 새로운 데이터를 사용해 주기적, 반복적으로 훈련해야 한다.
✅03-2 : 선형 회귀
- 선형 회귀 linear Regression
: 특성이 하나인 경우 어떤 직선을 학습하는 알고리즘.
from sklearn.linear_model import LinearRegression
lr = LinearRegression()모델 파라미터 (a,b)
[1차 방정식]
y = a * x + b
a : lr.coef_ (=기울기, 계수coefficient, 가중치weight)b : lr.intercept_ (=보정치)
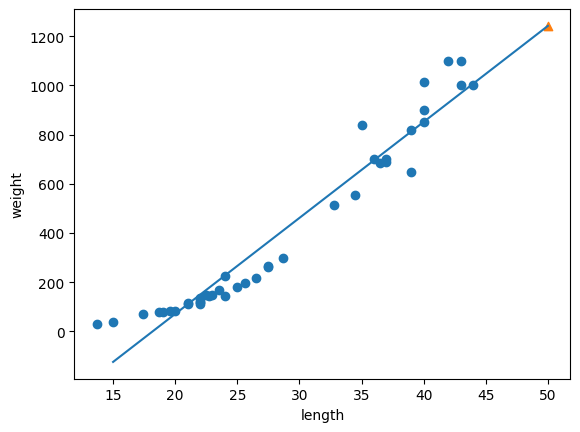
#훈련세트 plt.scatter(train_input, train_target) #농어 (15~50) 직선그래프 plt.plot([15,50],[15*lr.coef_+lr.intercept_, 50*lr.coef_+lr.intercept_]) #a*x + b #농어(50) 추가 plt.scatter(50, 1241.8, marker='^') plt.xlabel('length') plt.ylabel('weight')
- 다항 회귀 polynomial regression
: 최적의 곡선모델 파라미터 (a,b,c)
-> 이 때는 곱해지는 a,b가 가중치, c가 보정치[2차 방정식]
y = (a x^2) + (b x) + c

x^2 열 추가 train_poly = np.column_stack((train_input**2, train,input)) test_poly = np.column_stack((test_input**2, test_input)) lr = LinearRegression() lr.fit(train_poly, train_target) print(lr.predict([[50**2,50]])) #[1573.98423528] print(lr.coef_,lr.intercept_) #[1.01433211 -21.55792498] 116.0502107827827
✅03-3 : 특성 공학과 규제
[다중 회귀] multiple regression : 특성이 여러개인 선형 회귀
선형회귀는 특성이 많을 수록 좋다. 여러 특성을 다항회귀에 함께 적용하기!
-> 선이 아닌 평면을 학습
-> 그러나 특성이 너무 많으면 선형회귀 모델을 제약하기 위한 규제가 필요 (릿지 회귀, 라쏘 회귀의 'alpha' 등)
- 다중 회귀 적용
#특성 공학 : 기존의 특성을 사용해 새로운 특성을 뽑아내는 작업
#현재 perch_full = [[ length height width ]]
#perch_weight = weight
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(perch_full, perch_weight, random_state =42)
#주어진 특성을 조합해 새로운 특성을 만듦, 특성공학
# y= a*x_1 + b*x_2 + c*x_3 + d*1
# 특성은 (길이,높이,두께,1) -> 선형방정식의 절편은 '항상 값이 1인 특성'과 곱해지는 계수 d.
# But, sklearn 선형모델은 자동으로 절편(bias)을 추가하므로, 매개변수include_bias=False 지정.
# 매개변수degree=고차항의 최대 차수
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(include_bias = False)
# 예시 - 특성이 2,3 으로 이루어진 샘플
# 해 = [[2. 3. 4. 6. 9.]]
poly.fit([[2,3]])
print(poly.transform([[2,3]]))
#특성 추가하기 - degree 매개변수 사용
poly = PolynomialFeatures(degree=5, include_bias=False)
poly.fit(train_input)
train_poly = poly.transform(train_input)
test_poly = poly.transform(test_input)
print(train_poly.shape)
# (42, 55) 특성개수 엄청 늘어남
lr.fit(train_poly, train_target)
print(lr.score(train_poly, train_target))
print(lr.score(test_poly, test_target))
# 0.9999999999996433
# -144.40579436844948 >>> 엄청난 과대적합 발생
-> 해결법 : 1)특성 줄이기 / 2)정규화스케일링 & 규제 모델 사용
- 정규화 Normalization
: 특성의 스케일을 서로 맞추어 곱해지는 계수값의 차이를 줄이는 전처리 과정.
-> 보다 공정하게 제어 가능
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_poly)
train_scaled = ss.transform(train_poly)
test_scaled = ss.transform(test_poly)- 규제 regularization
: 머신러닝 모델 훈련세트의 과대적합 방지.
ex) 선형회귀 모델의 경우, 특성에 곱해지는 계수(=기울기)의 크기를 작게 만듦
-> 보다 보편적인 패턴 학습
[선형회귀 모델에 규제를 추가한 모델 : 릿지, 라쏘]
-> 계수를 줄인다. 하이퍼파라미터 매개변수인 'alpha='로 조정.
-> 적절한 alpha 값을 찾기 위해, alpha 값에 대한 R^2 값의 그래프 그려보기.
-> 훈련 세트 & 테스트 세트 점수가 가장 가까운 지점이 최적의 alpha값
- 릿지회귀 Ridge : 계수를 제곱한 값 기준으로 규제 적용
from sklearn.linear_model import Ridge
train_score = []
test_score = []
alpha_list = [0.001,0.01,0.1,1,10,100]
for alpha in alpha_list:
#릿지 모델 만들기
ridge = Ridge(alpha=alpha)
#릿지 모델 훈련
ridge.fit(train_scaled, train_target)
#훈련점수, 테스트점수 저장
train_score.append(ridge.score(train_scaled, train_target))
test_score.append(ridge.score(test_scaled, test_target))
#alpha_list 를 로그 함수로 바꾸어 지수로 표현. 10단위라 log10사용
#각각의 값을 동일한 간격으로 나타내기 위함 (각각 -3~2로 순차배정)
#np.log() : 자연상수 e를 밑으로 하는 자연로그
#np.log10() : 10을 밑으로 하는 상용로그
plt.plot(np.log10(alpha_list), train_score)
plt.plot(np.log10(alpha_list), test_score)
plt.xlabel('alpha')
plt.ylabel('R^2')
plt.show()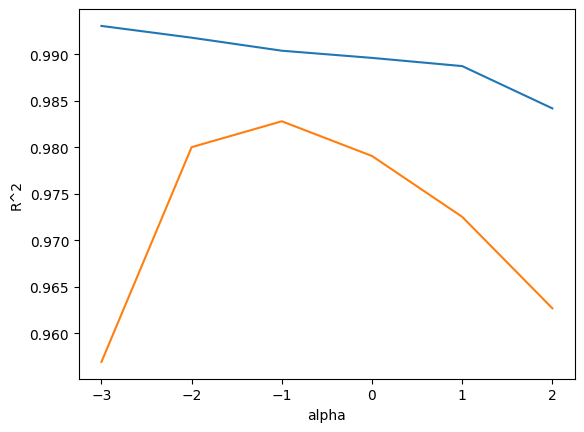
-> 각 alpha 값일 때 반환하는 결정계수 값 R^2 그래프
-> alpha 값이 -1 일 때 (alpha_list의 10^-1=0.1 값일 때) 두 그래프가 가장 가깝고, 테스트 세트 점수가 가장 높다.
#최적의 alpha로 재훈련
ridge = Ridge(alpha=0.1)
#릿지 모델 훈련
ridge.fit(train_scaled, train_target)
#훈련점수, 테스트점수
print(ridge.score(train_scaled, train_target))
print(ridge.score(test_scaled, test_target))```
>0.9903815817570367
>0.9827976465386928- 라쏘 Lasso : 계수의 절댓값을 기준으로 규제 적용
해당 클래스는 최적의 모델을 찾기 위해, 좌표축을 따라 최적
화를 수행해가는 좌표 하강법 coordinate descent를 사용
max_iter=1000(기본값) : 알고리즘의 수행 반복 횟수를 지정
print(np.sum(lasso.coef_==0))
-> 라쏘 모델의 계수는 coef에 저장되어있다.
계수 값을 0으로 만든 것의 결과가 출력된다.
[모델]
1. 데이터 준비
2. 사이킷런-변환기 (다중특성. 특성공학)
3. 사이킷런-다중회귀모델훈련
(회귀모델은 전부 linear_model import LinearRegression)
4. 스케일링(정규화), 규제모델 지정
5. 릿지회귀 / 라쏘회귀 모델 사용
6. 하이퍼파라미터(여기서는 alpha) 값 조정
