1.연관성분석
연관성분석(Association AnaIysis)
- 조사 대상에서 수집한 자료의 적도를 기준으로 변수들 간에 어느 정도 밀접한 관계가 있는지를 판단하기 위한 분석 방법
- 자료의 적도를 기준으로 변수 간의 연관성을 파악하기 때문에
척도에 따라 연관성 분석 방법도 달라짐
- 연속형 적도 : 피어슨 상관분석
- 범주형 척도 : 교자분석
1. 상관분석(Correlation Analysis)
- 조사 목적에 맞게 구성된 변수들 간의 연관성을 분석하는 방법
- 상관관계는 두 개의 변수를 기준으로 양의 방향과 음의 방향으로 일정한 규칙이 나타나는 선형관계의 형태와 연관 정도를 수치로 표현한 것
- 예. 키와 몸무게의 관계, 광고비와 매출액의 관계, 흡연과 수명의 관계
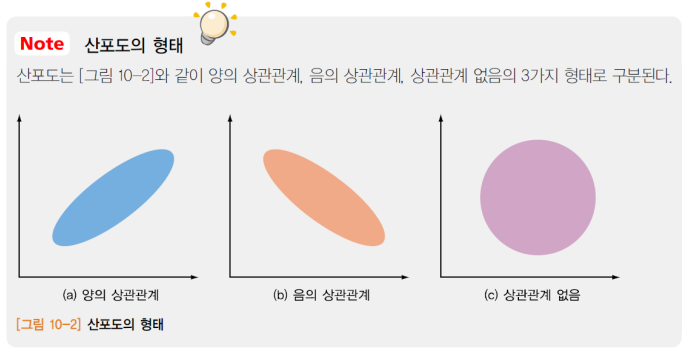
1. 산포도(Scatter Diagram)
- 두 개의 변수를 x와y의 그래프로 나타내어,이들의분포 정도를확인
- 표본이 가지는 중심 경향을 파악한 후, 표본이 분포하고 있는 정도를 나타낸 것

# data 입력
ht <- c(160,155,165,166,170,176,169,169,180,178)
wt <- c(55,49,57,58,65,66,66,60,77,70)# 산점도 그리기
plot(ht, wt)
# ggplot2 이용
dt <- data.frame(ht, wt)
ggplot(dt, aes(x=ht, y=wt)) + geom_point()2. 상관계수(Correlation Coefficient)
- 공분산 : 두 개의 확률변수에 대한 흩어짐의 정도가 동일한 방향인 양(+) 의 방향인지 혹은 반대 방향인 음(-)의 방향인지를 나타내는 수치
- 상관계수 : 공분산의 표준화
- 두 변수가 서로 변하는 정도를 수치로 나타낸 것
- 예. x가 변하면y는 어떻게 변하는지를 표현
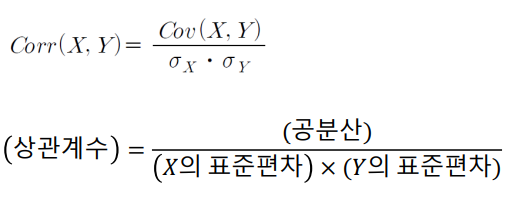
A”와 Y가 서로 양(+)의상관관계를가지면상관계수는0< Corr(X, Y) < 1의 값을 가지며.X와Y가 사로 음(-)의 상관관계를 가지면 상관계수는-1 < Corr(X,Y) <0의 값을 가진다. X와 Y가 일정한 규칙 없이 (+)값과 (-)값이 동시에 대응하면 상관계수는 0이다.

# 상관계수를 구하고 분석
cor.test(ht, wt)# 예제
# data 입력
m<-matrix(c(1:10, (1:10)^2), ncol=2)
> m
[,1] [,2]
[1,] 1 1
[2,] 2 4
[3,] 3 9
[4,] 4 16
[5,] 5 25
[6,] 6 36
[7,] 7 49
[8,] 8 64
[9,] 9 81
[10,] 10 100
# 산포도 그리기
# 상관계수를 구하고 분석2. 교차분석(Cross-tabulation Analysis)
-
범주형으로 구성된 자료듬 간의 연관관계를 확인하기 위해 교자표를
-
만들어 관계를 확인하는 분석 방법
-
변수들의빈도(frequency)를 이용하여상호 연관성을판단
-
검정통계량: 카이제곱 통계량
-
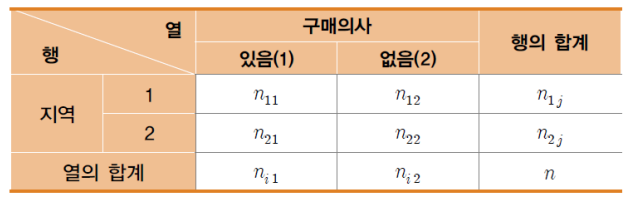
교자표 (Cross-tabuIation, Contingency TabIe)
-
2개의 조사 요인에 대한 자료값을 각각 행과 열로 배열하여 교자되
는 항목에 대한 빈도를 나타낸 표 -
교자표의 행과 열에 범주형 변수를 구분하여 입력
-
서로 연관성이 있는 빈도를 확인할 수 있음
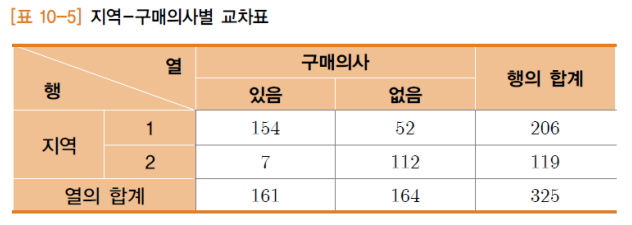
독립성검정(lndependence Test)
-
여러 범주를 대상으로 각 범주들이 독립적인지를 판단하는 검정 방법
-
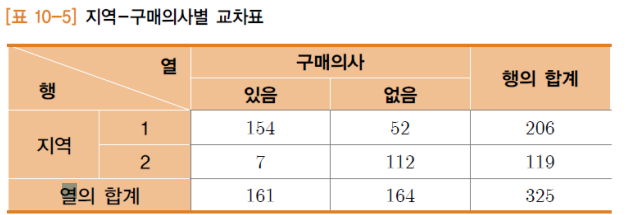
예. 어떤 상품에 대하여 지역과 구매의사는 서로 독립인가?
동질성검정(homogeneity Test)
- 여러 모집단에서 추출한 표본의 분포가 비슷한지 알아보는 검정
• 예. 어떤 상품의 구매 의사는 지역과 상관없이 일정한 분포를 따르는가?
적합도검정(Goodness-of-fit Test)
- 실험 또는 조사 결과가 이론적으로 주어진 분포를 따르는지 검정
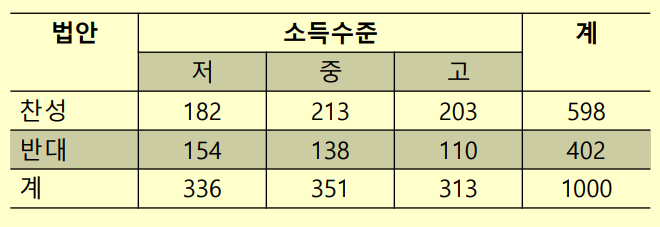
예제1. 다음은 어떤 법안에 대한 찬반 결과를 투표자의 소득 수준에 따라 분류한 분할표이다. 소득 수준에 따른 찬반 결과가 서로 독립인지 검정하라.
# data 입력
income <- c(182,213,203,154,138,110)
level <- c("1.low","2.middle","3.high","1.low","2.middle","3.high")
opinion<- c("1.yes","1.yes","1.yes","2.no","2.no","2.no")
# table 형태로 변경
sample.table <- xtabs(income ~ opinion + level)
sample.table# 분할표 검정을 위해 "gmodels" package 설치
install.packages("gmodels")
library(gmodels)
# Contingency Table 검정
CrossTable(sample.table, expected = TRUE)
# Chi-square Test
chisq.test(sample.table)예제2. 주사위를 120번 던져 각 눈이 나온 횟수가 다음과 같았다.
이를 토대로 주사위가 공정한지 검정하라

# data 입력
x=c(31,26,22,18,13,10)
# 카이제곱 검정
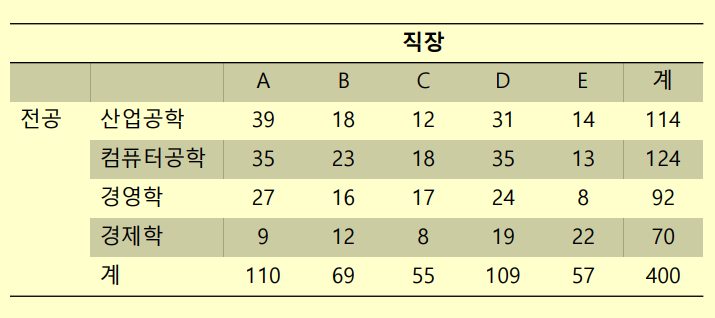
chisq.test(x)예제3. 대학생 400명을 대상으로 희망하는 직장과 전공을 조사한 결
과가 다음 표와 같다.
희망하는 직장과 전공은 서로 관계가 있는가?
2. 회귀분석
1. 회귀분석
1. 회귀분석 용어
- 독립변수 (lndependent VariabIe)
- 연구나 조사의 연구모텔에서 변수에 일어나는 현상을 설명하거나 원인이 되어 다른 변수에 영향을 주는 변수
- 설명변수 (ExpIanatory VarlabIe)
- 종속변수 (Dependent Variable)
- 연구나 조사의 연구모텔에서 설명되거나 결과가 되어 다른 변수로부터 영향을 받는 변수
- 반응변수(Response Variable)

2. 회귀분석 예제
- 증권회사에서는 미래의 주식 시세를 예측하기 위해 많은 연구
- 주식 시세는 기업의 매출액, 원유가격, 국제정세, 정부정책 발표 등 매우 많은 요인들에 의해 영향 받음
• 독립변수 : 주식시세에 영향을 미치는 요인들
• 종속변수 : 독립변수의 영향에 따라 값이 결정되는 주식시세
3. 회귀분석 용어
- 예측모텔 (Prediction Model) 또는 예측모형
- 독립변수에 해당하는 자료와 종속변수에 해당하는 자료를 모아 관계를 분석하고 이를 예측에 사용할 수 있는 통계적 방법
- 회귀분석 (Regression Analysis)
- 회귀 이론을 기초로 독립변수(설명변수)가 종속변수(반응변수)에 미치는 영향을 파악하여 예측 모텔을 도출하는 통계적 방법

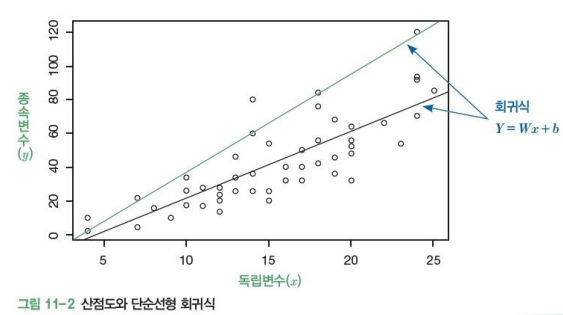
2. 단순선형회귀분석 (Simple Linear Regression Analysis)
- 독립변수(X)와 종속변수(Y) 사이의 선형관계를 파악하고 이를 예측에 활용하고자 함
- 회귀식을 이용하여 변수 X를 원인으로 Y가 어떻게 될지 추정하거나 설명하는 것이 목적
- 예. 기온(X) 자료를 이용하여 아이스크림 판매량(Y)을 예측하는문제
- 1자식의 형태를 가짐
- y =ax + b
a: 기울기
b: y절편
3. R을 이용한 선형회귀모형
주행속도와 제동기리 사이의 회귀모형 구하기
- lm(y~x,data="dataset이름”)
- y:종속변수
- x:독립변수
# car 자료 이용
head(cars)
# 산점도를 통해 선형 관계 확인
plot(dist~speed, data=cars)# 회귀모형 구하기
model <- lm(dist~speed, cars)
model
# 회귀선을 산점도 위에 표시
abline(model)
# y절편
coef(model)[1]
# 기울기
coef(model)[2]# 예측값 구하기
b <- coef(model)[1]
a <- coef(model)[2]
speed <- 30
dist <- a*speed + b
dist
speed <- 35
dist <- a*speed + b
dist
speed <- 40
dist <- a*speed + b
dist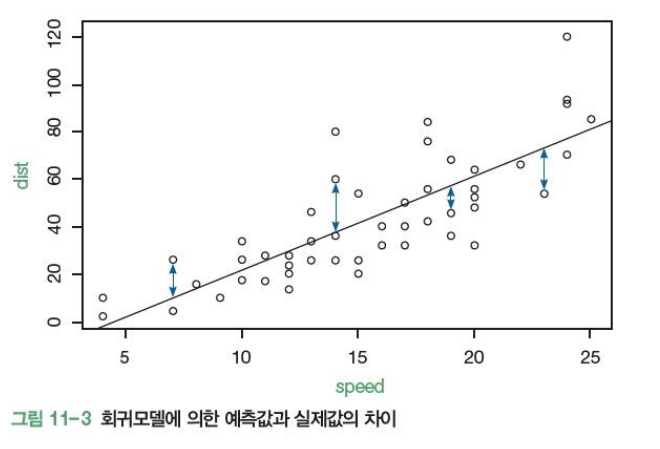
# 실제 주행속도
speed <- cars[,1]
# 예상 제동거리
pred <- a * speed + b
pred
# 오차
compare <- data.frame(pred, cars[,2], pred-cars[,2])
colnames(compare) <- c('예상','실제','오차')
head(compare)4. 예제. iris 데이터를 이용한 선형회귀모형
# 산점도 그리기
# plot( ), pairs( )
plot(iris[1:4],main="scatter diagram")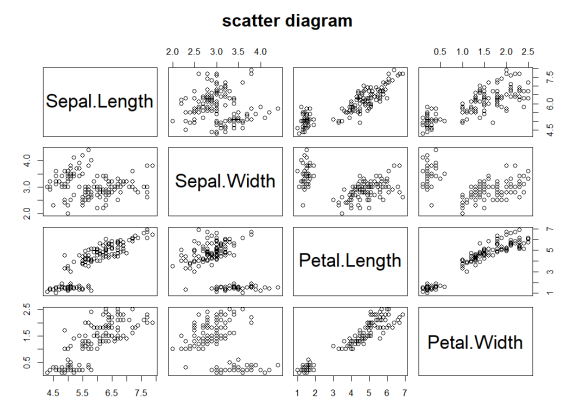
# 산점도 그리기
# plot( ), pairs( )
plot(iris[1:4],main="scatter diagram")
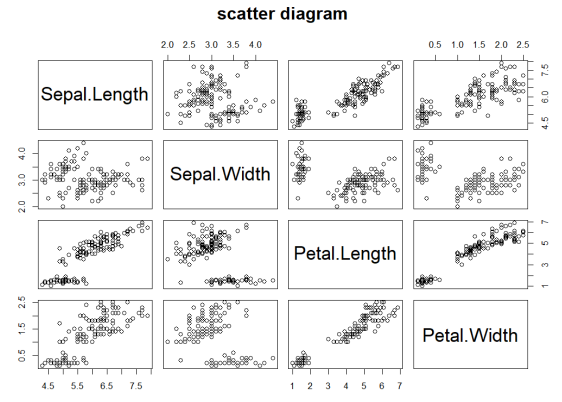
pairs(iris[1:4],main="scatter diagram")
pairs(~Sepal.Length+Sepal.Width+Petal.Length+Petal.Width,
data=iris,main="scatter diagram")pairs(iris[1:4],upper.panel=NULL,main="scatter diagram")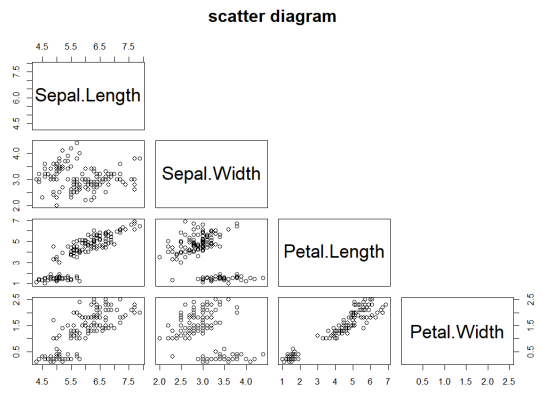
# 산점도 그리기
# plot( ), pairs( )
plot(iris[1:4],main="scatter diagram")
# 선형회귀모형
model2 <- lm(Petal.Length ~ Petal.Width, iris)
summary(model2)
# estimates : 각 변수의 coefficients
# p-value : coefficients의 유의성 판단
# R-squared : 모형의 설명력
# F-statistic, p-value : 모형의 유의성 판단
# 추정된 회귀모형
model2$coef
model2$fitted
model2$resid
