이원 분산분석(Two-way ANOVA)

강림·2023년 12월 11일
R데이터분석분산분석
0

Data Analysis

목록 보기
10/13
post-thumbnail

1.이원분산분석(Two-wayANOVA)

1. 분산분석 구분

  • 3개 이상의 집단에 대한 평균 사이를 알아보는 검정
  • 독립변수와 종속변수의 개수에 따른 종류 구분

2. 이원 분산분석

  • 두 가지 요인을 기준으로 집단 간 사이를 조사하는 것
  1. 2개의 독립변수에 따른 종속변수의 평균 사이를 검증
  2. 2개 독립변수 간 상호작용 효과를 검증
  • 상호작용0nteraction) : 종속변수에영향을 미치는두 독립변수 간의 시너지
    효과
    • 독립변수 : 2개의 범주형 자료
    • 종속변수 : 1개의 연속형 자료

3. 효과(effect)

  • 분산분석의 주요 작업 : 셋 이상의 집단 간 차이를 검정
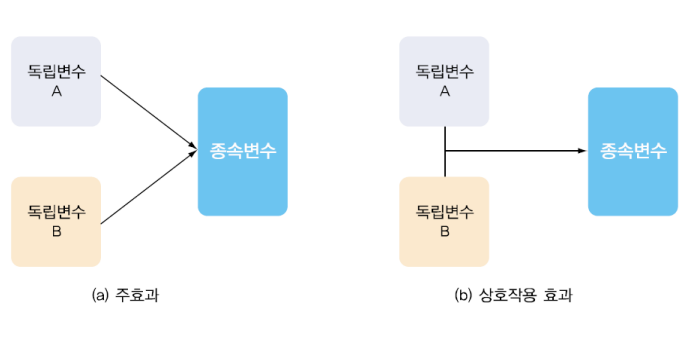
  • 주효과(m해n effect) : 단일 요인과 관련된 결과
  • 상호작용 효과(interaction effect) : 두 요인의 영향을 같이 다루는 것. 즉, 두 개의 독립변수가 동시에 작용하여 종속 변수에 미치게 되는 영향

성별(남성,여성)과 치료 방법(고강도, 저강도 운동)의 두 가지 요인과 결과 변수(체중감량)를 포함한 실험 설계

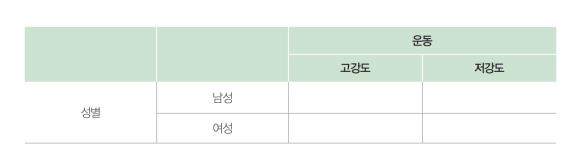
  • 운동 강도의 수준 간 체중 감량 정도에 사이가 존재하는가?
    • 주효과
  • 남성과 여성의 성별 간에 체중 감량 정도에 차이가 존재하는가?
    • 주효과
  • 남성 또는 여성에 대한 운동 강도 수준의 효과는 무엇인가?
    • 상호작용 효과

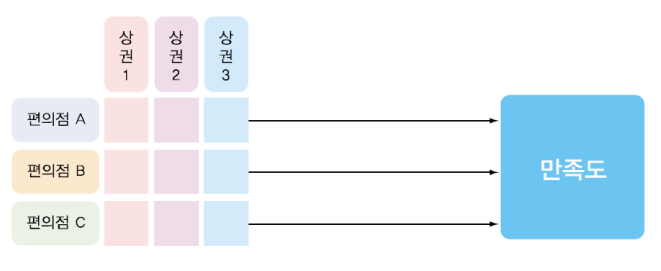
편의점별(A,B,C)과 상권별(강남,홍대,종로)의 두 가지 요인과 결과 변수(만족도)를 포함한 실험 설계

  • 원인이 되는 변수 (독립변수)
  1. 편의점종류(3개)
  2. 상권(3개)
  • 결과가되는 변수 (종속변수)
    • 소비자의 만족도
  • 편의점 종류 간 소비자의 만족도 차이가 존재하는가?
  • 강남, 홍대, 종로의 상권별 간에 소비자의 만족도 차이가 존재하는가?
  • 각각의 편의점 종류에 대한 상권별 효과는 무엇인가?

4. 이원 분산분석의 과정

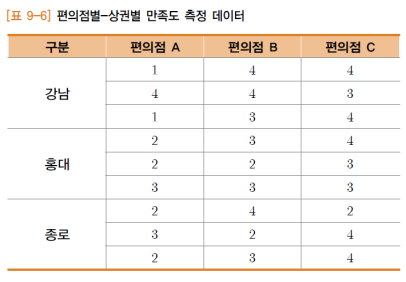
Q. 두 독립변수에 대한 소비자 만족도에 사이가 있는지 여부를 유의수준 5%에 대해 검정하라.

1. 가설 수립

조사의 목적이 편의점별, 상권별 두 독립변수에 대해 소비자 만족도에 사이가 있는지에
맞취져 있으므로 가설은 기본적으로 2개이고 상호작용을 생각하면 총 3개의 가설을 수립
할수 있다.

  • 가설 1 : 편의점별 소비자 만족도의 사이는 없다.
  • 가설 2 : 상권별 소비자 만족도의 사이는 없다.
  • 가설 3 : 각각의 편의점 종류에 대해 상권별 효과는 없다.

2. 검정통계량 계산

  • 이원 분산분석에서도 평균의 차이를 확인하기 위하여 '분산(편자)'를 계산
  • 총편자는 여러 개의 편자로 나눠서 생각할 수 있음

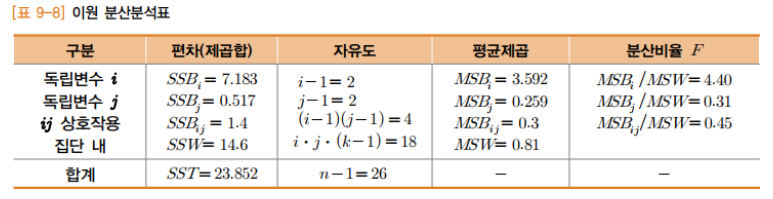
3. 의사 결정



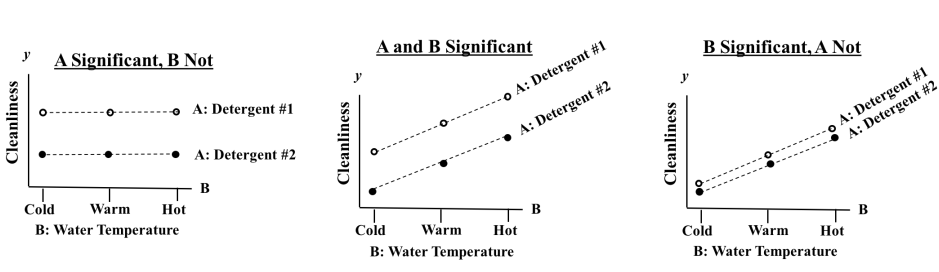
5. 주효과, 상호작용 효과

  • 독립변수 : A(세제의 종류 : #1 , #기, B(세탁 온도 : Hot, Warm, Cold)
  • 종속변수 : 청결도

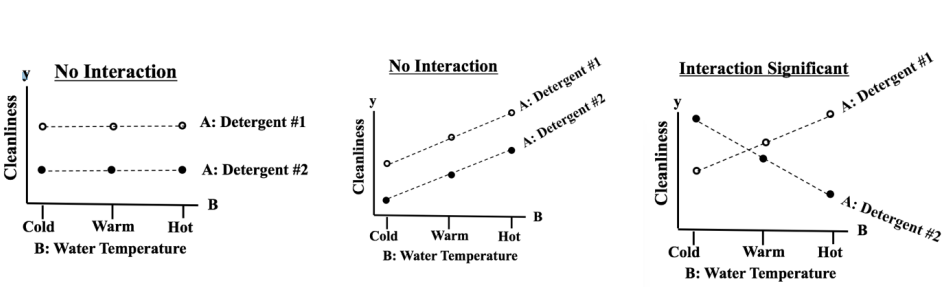
  • 독립변수 : A(세제의 종류 : #1 , #기, B(세탁 온도 : Hot, Warm, Cold)
    y
  • 종속변수 : 청결도

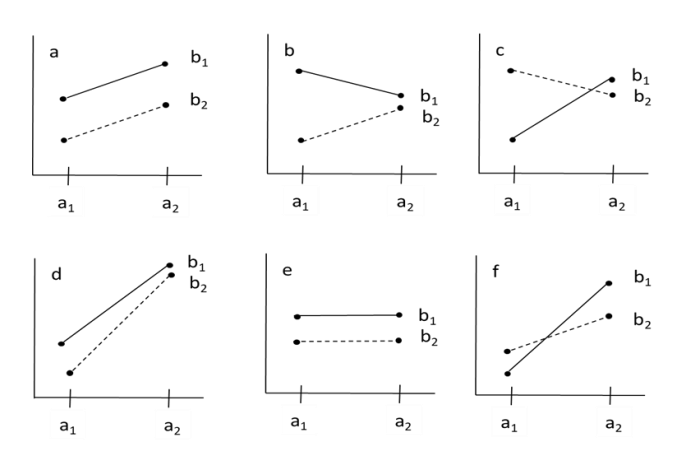
6. 가정사항

  • 분산분석은 모든 모집단이 정규성을 가지고 모든 집단의 분산이 같다고 가정

    2. 이원분산분석R예제

    1. 상호작용 없는 이원 분산분석

  • aov(y~x1+x2, data="dataset이름")

  • Y : 정량적인수치

  • x1 : 첫 번째 요인변수(factor)

  • x2 : 두 번째 요인변수

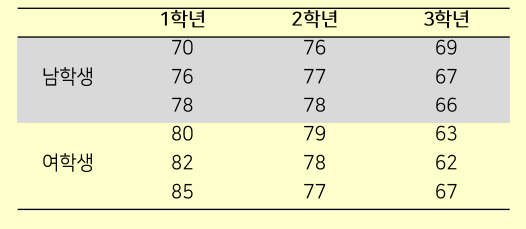
#다음 자료를 대상으로 학년별, 성별로 성적의 차이가 있는지 검정하라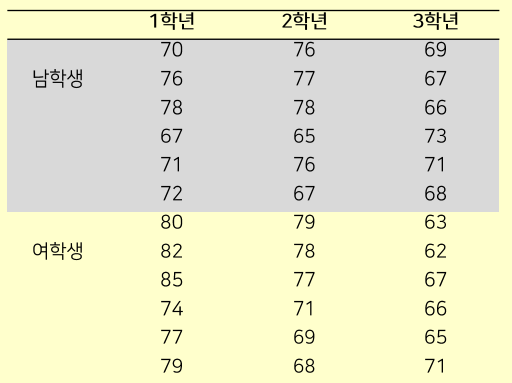

# data 입력
score01 <- c(70,76,78,80,82,85)
score02 <- c(76,77,78,79,78,77)
score03 <- c(69,67,66,63,62,67)
scoreAll <- c(score01,score02,score03)
# 학년 label 만들기
grade <- c(rep(1,6),rep(2,6),rep(3,6))
# 성별 label 만들기
gender <- rep(c('male','male','male','female','female','female'),3)
# 학년을 수치 data에서 요인변수(factor)로 변경
grade <- factor(grade)
sampleData <- data.frame(scoreAll,grade,gender)
sampleData
scoreAll grade gender
1 70 1 male
2 76 1 male
3 78 1 male
16 63 3 female
17 62 3 female
18 67 3 female
# 학년별, 성별 평균
tapply(sampleData$scoreAll,list(sampleData$grade,sampleData$gender), m
ean)
female male
1 82.33333 74.66667
2 78.00000 77.00000
3 64.00000 67.33333
# 학년별, 성별 표준편차
tapply(sampleData$scoreAll,list(sampleData$grade,sampleData$gender), sd
)
female male
1 2.516611 4.163332
2 1.000000 1.000000
3 2.645751 1.527525
# 분산분석
result01 <- aov(scoreAll~grade+gender, data=sampleData)
summary(result01)
 Df Sum Sq Mean Sq F value Pr( >F)
grade 2 611.4 305.72 26.402 1.78e-05 ***
gender 1 14.2 14.22 1.228 0.286
Residuals 14 162.1 11.58
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# TukeyHSD 사후비교
TukeyHSD(result01)
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = scoreAll ~ grade + gender, data = sampleData)
$grade
 diff lwr upr p adj
2-1 -1.00000 -6.141999 4.141999 0.8682151
3-1 -12.83333 -17.975333 -7.691334 0.0000372
3-2 -11.83333 -16.975333 -6.691334 0.0000872
$gender
 diff lwr upr p adj
male-female -1.777778 -5.218267 1.662712 0.2864267

2. 상호작용 있는 이원 분산분석

  • aov(y~x1+x2 x1:x2, data="dataset이름")
    -Y : 정량적인수치
    • x1 : 첫 번째 요인변수(factor)
    • x2 : 두 번째 요인변수
    • x1 :x2 : x1과 x2의 상호작용

# data 입력
score01 <- c(70,76,78,67,71,72,80,82,85,74,77,79)
score02 <- c(76,77,78,65,76,67,79,78,77,71,69,68)
score03 <- c(69,67,66,73,71,68,63,62,67,66,65,71)
scoreAll <- c(score01,score02,score03)
# 학년 label 만들기
grade <- c(rep(1,12),rep(2,12),rep(3,12))
# 성별 label 만들기
gender <- rep(c(rep('male',6),rep('female',6)),3
# 학년을 수치 data에서 요인 변수로 변경
grade <- factor(grade)
sampleData <- data.frame(scoreAll,grade,gender)
sampleData
scoreAll grade gender
1 70 1 male
2 76 1 male
3 78 1 male
.
.
33 67 3 female
34 66 3 female
35 65 3 female
36 71 3 female
# 학년별, 성별 평균
tapply(sampleData$scoreAll,list(sampleData$grade,sampleData$gender), m
ean)
female male
1 79.50000 72.33333
2 73.66667 73.16667
3 65.66667 69.00000
# 학년별, 성별 표준편차
tapply(sampleData$scoreAll,list(sampleData$grade,sampleData$gender), sd
)
female male
1 3.834058 4.033196
2 4.885352 5.636193
3 3.204164 2.607681

#분산분석
result02 <- aov(scoreAIIN grade 十gender 十grade:gender, data=sampIeData)
summary(result02)
Df Sum Sq Mean Sq
grade
gender
2 467.7
1 18.8
233.86
18.78
84.69
17.28
Fvalue
13.535
1.087
4.902
Pr(>F)
6.47e-05 ***
0.3055
grade:gender 2 169.4 0.0144 *
Residuals 30 518.3
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 " 1
# TukeyHSD 사후비교
TukeyHSD(result02)
Tukey multiple comparisons of means
 95% family-wise confidence level
Fit: aov(formula = scoreAll ~ grade + gender + grade:gender, data = sampleD
ata)
$grade
 diff lwr upr p adj
2-1 -2.500000 -6.683435 1.683435 0.3177788
3-1 -8.583333 -12.766768 -4.399898 0.0000574
3-2 -6.083333 -10.266768 -1.899898 0.0032814
# 등분산 검정을 위해 library 설치 및 불러오는 과정
install.packages("car")
library(car)
# Levene's Test를 이용하여 등분산 검정
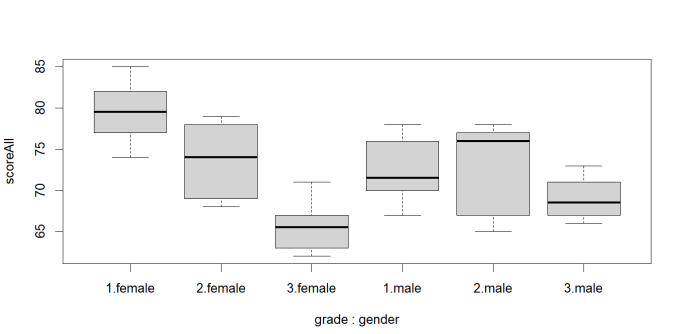
leveneTest(scoreAll ~ grade*gender,data=sampleData)
# boxplot
boxplot(scoreAll~gender*grade,data = sampleData)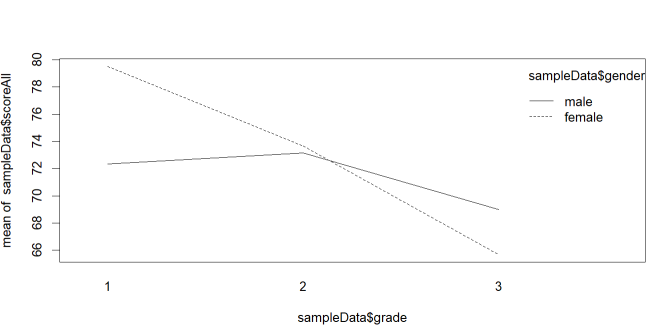

# Interaction plot
interaction.plot(x.factor=sampleData$grade, # x축에 사용할 변수
 trace.factor=sampleData$gender, # 선으로 표현될 변수
 response=sampleData$scoreAll)

업로드중..

profile
강림
DRUDGER
이전 포스트

등분산검정

다음 포스트

연관성 분석

0개의 댓글