통계 기초 (가설 검정, 시계열 분석)

1. 가설 검정

• 가설(Hypothesis): 주어진 사실 또는 조사하려고 하는 사실에 대한 주장
  • 귀무 가설(Null Hypothesis; $H_{0}$): 기존에 널리 알려진 사실, 연구 목적이 아님 ex) A 백신은 효과가 없다.
  • 대립 가설(Alternative Hypothesis; $H_{1}$): 새로운 사실, 연구 목적에 해당함 ex) A 백신은 효과가 있다.
• 오류: 귀무가설 또는 대립가설을 잘못 기각하는 상황
  • 제1종 오류(Type 1 Error): 귀무가설이 참이나, 귀무가설을 기각하는 오류
  • 제2종 오류(Type 2 Error): 대립가설이 참이나, 대립가설을 기각하는 오류
• 검정 통계량: 귀무가설이 참이라는 가정 하에 계산한 통계량
• P-value: 귀무가설이 참일 확률
• 기각역: 귀무가설을 기각시키는 검정통계량의 관측값 영역

2. 검정 종류

• 양측 검정(Two-side Test): '평균이 0과 같지 않다'와 같이 양쪽 방향에 대한 주장
• 단측 검정(One-side Test): '평균이 0보다 작다'와 같이 한쪽 방향에 대한 주장

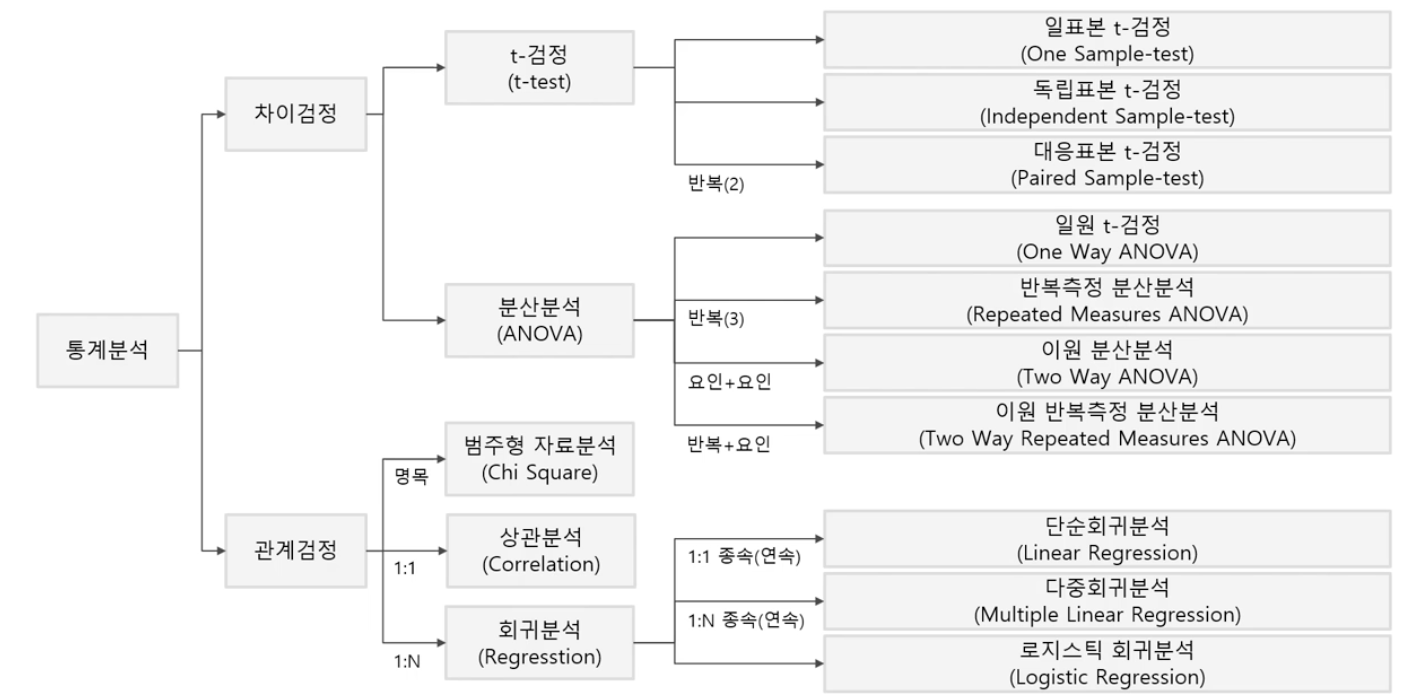
3. 주요 검정방법

4. 범주형 자료 검정

• 적합도 검정(Goodness of Fit): 관측된 값들이 특정 분포를 따르고 있는가?
• 독립성 검정(Test of Independence): 두 요인 간 관련이 있는가?
• 동질성 검정(Test of Homogeneity): 세 개 이상의 모집단에서 관측된 값들이 동일한 비율을 나타내고 있는가?

5. 수치형 자료 검정

• 상관관계 분석: 두 변수 간 유의미한 상관관계가 존재하는가?
• 회귀 분석: 독립변수로 종속변수로 예측하는 회귀 모형을 만드는 분석 기법으로, 회귀선으로부터 각 관측치의 오차를 최소로 하는 선을 찾음(최소제곱법; Method of Leaset Squares)
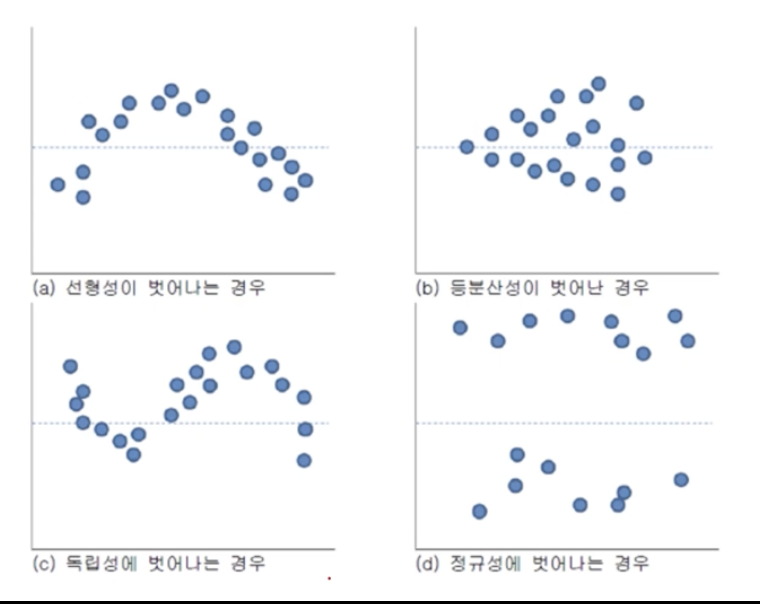
  • 선형성 가정: 종속변수와 독립변수는 선형관계에 있어야 함
  • 정규성 가정: 오차항은 평균이 0인 정규 분포를 따라야 함
  • 등분산성 가정: 오차항의 분산은 독립변수에 관계 없이 일정하여야 함
  • 독립성 가정: 모든 오차항은 서로 독립이어야 함
    
• t 검정: 두 모집단의 평균 차이를 검정
• 분산 분석: 셋 이상의 모집단의 평균 차이를 검정

6. 시계열 분석

• 시간의 흐름에 따라 기록된 데이터(시계열 데이터)를 분석하는 기법
• 이동평균(Moving Average) 모형: 최근 데이터의 평균으로 예측하는 기법
• 자기상관(Autocorrelation) 모형: 변수의 과거 값의 선형 조합으로 예측하는 기법
• ARIMA 모형: 과거 값과 오차를 사용해서 예측하는 기법
• 지수평활법: 현재와 가까운 과거 값일수록 많은 가중치를 주어 미래를 에측하는 기법

*이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다.