통계 기초 (통계량, 확률, 확률분포)

1. 통계학이란?

• 산술적 방법을 기초로 하여, 주로 다량의 데이터를 관찰하고 정리 및 분석하는 방법을 연구하는 수학의 한 분야
  • 기술통계학(Descriptive Statistics): 데이터를 수집하고 수집된 데이터를 쉽게 이해하고 설명할 . 수있도록 정리 요약 설명하는 방법론
  • 추론통계학(Inferential Statistics): 모집단으로부터 추출한 표본 데이터를 분석하여 모집단의 여러가지 특성을 추측하는 방법론

2. 변수와 데이터

• 변수: 어떤 정해지지 않은 임의의 값을 표현하기 위해 사용된 기호, 특정 변수에 대해 관측된 값이 자료에 해당
• 질적(Qualitative) 자료: 몇 개의 범주로 구분할 수 있는 데이터 ex) 성별, 업종 등
• 양적(Quantitative) 자료: 숫자의 형태를 띄며 숫자의 크기가 의미를 갖는 데이터 ex) 몸무게, 나이 등

3. 통계량

• 표본으로 산출한 값으로, 기술통계량이라고도 표현함
• 통계량을 통해 데이터(표본)가 갖는 특성을 이해할 수 있음

4. 중심경향치

• 표본의 중심을 설명하는 대표값을 말함
• 평균(Average): 관측치의 합을 관측치의 개수로 나눈 값
• 중앙값(Median): 관측치를 크기 순으로 나열했을 때, 가운데 위치하는 값
• 최빈값(Mode): 관측치 중에서 가장 많이 관측되는 값

5. 산포도

• 데이터가 흩어진 정도를 나타내는 값을 말함
• 범위(Range): 데이터의 최대값과 최소값의 차이
• 사분위수(Quartile): 데이터를 오름차순으로 정렬하여 4등분 하였을 때, 각 부분(25%, 50%, 75%, 100%)에 위치하는 값
• 백분위수(Percentile): 데이터를 오름차순으로 정렬하여 100등분 하였을 때, 각 부분인 p%에 위치하는 값
• 분산(Variance): 데이터의 분보가 얼마나 흩어져 있는지 나타내는 값
• 표준편차(Standard Deviation): 분산의 제곱근에 해당되는 값
• 변동계수(Coefficient of Variation; CV): 표준편차를 평균으로 나눈 값

6. 왜도와 첨도

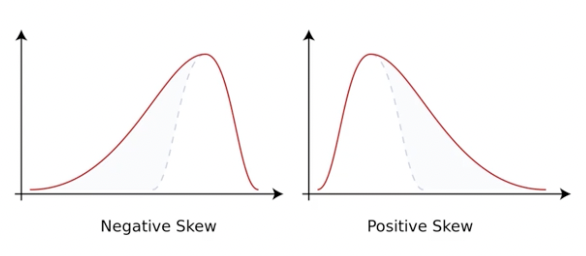
• 왜도(Skew): 자료의 분포가 얼마나 좌우 비대칭인지 표현하는 지표
  
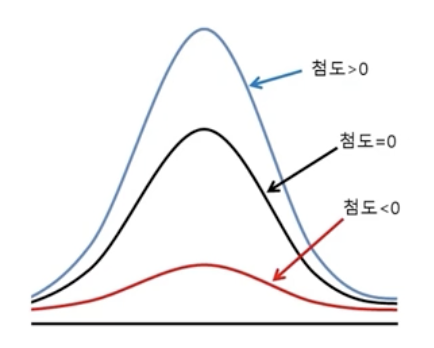
• 첨도(Kurtosis): 확률분포의 꼬리가 두꺼운 정도를 나타내는 지표
  

7. 확률

• 표본 공간(Sample Space): 어떤 실험에서 나올 수 있는 모든 가능한 결과의 집합 ex) 동전 던지기의 표본공간 = {앞면, 뒷면}

• 확률(Probability): 모든 경우의 수에 대한 특정 사건이 발생하는 비율
  $P(A)=\frac{사건\,A가\,일어날\,경우의\,수}{표본공간\,S의\,경우의\,수}$

• 확률의 덧셈법칙: $P(A\cup B) = P(A) + P(B) - P(A\cap B)$

• 조건부 확률: 어떤 사건 A가 발생한 상황에서 또 하나의 사건 B가 발생할 확률
  $P(B|A)=\frac{P(A\cap B)}{P(A)}, P(A)\neq0$

8. 확률 변수

• 표본 공간에서 각 사건에 실수를 대응시키는 함수, 즉 시행의 결과에 따라 값이 정해지는 변수
• 이산 확률 변수: 셀 수 있는 값으로 구성되거나 일정 범위로 나타나는 경우
• 연속 확률 변수: 연속형 또는 무한대와 같이 셀 수 없는 경우
• 확률 변수 자체는 대문자(X, Y 등)로 표현하며, 확률 변수의 특정 값은 소문자(x, y 등)로 표현함
• 기댓값: 확률 변수의 평균에 해당되며, 기대되는 값
  $\mathbb{E}[X] = \sum_{i=1}^{n} x_i \cdot p_i$

9. 확률 분포

• 확률 변수 X가 취할 수 있는 모든 값과 그 값을 나타낼 확률을 표현한 함수

10. 이산형 확률분포

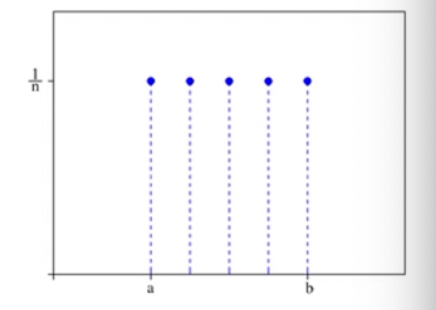
• 균등 분포: 확률 변수 X가 유한하고, 모든 확률변수에 대해 균일한 확률을 갖는 분포
  
• 베르누이 분포: 결과가 성공, 실패의 두 가지 결과만 존재하는 시행에 대하여, 확률변수가 갖는 분포
• 이항 분포: 연속적인 베르누이 시행을 n번 거쳤을 때, 성공한 횟수의 확률 분포
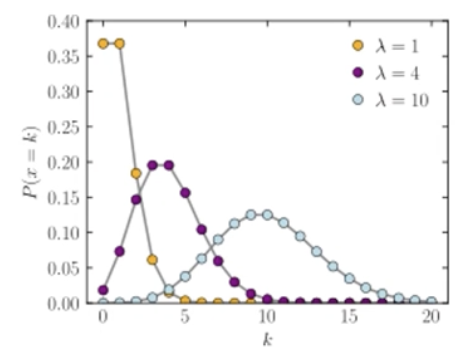
• 포아송 분포: 단위 시간동안 특정 사건이 몇 번 발생하는지 나타내는 확률 분포
  
• 기하 분포: 어떤 실험에서 처음 성공이 발생하기까지 시도한 횟수의 확률 분포
• 음이항 분포: 어떤 실험의 성공확률이 p일 때, r번의 실패가 나올 때까지 발생한 성공 횟수의 확률 분포

11. 연속형 확률분포

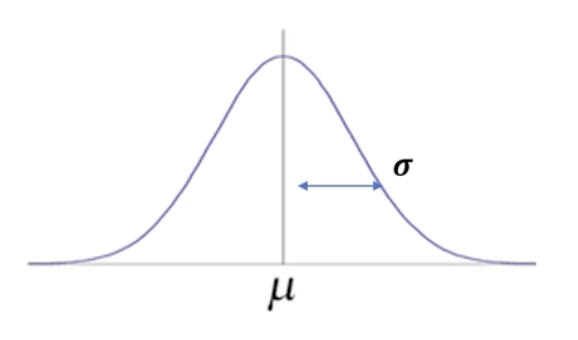
• 정규 분포: 평균을 중심으로 좌우 대칭 형태를 보이는 확률 분포
  
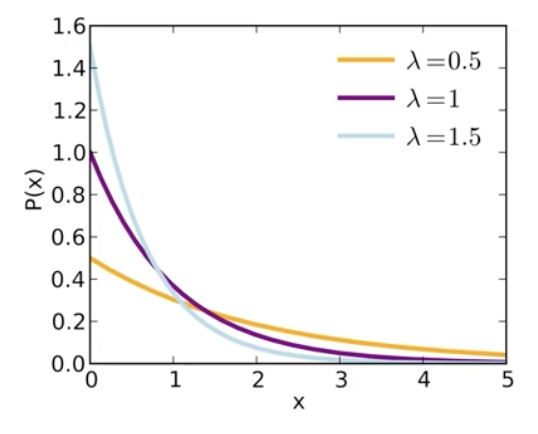
• 지수 분포: 단위 시간당 발생 확률이 $\lambda$인 어떤 사건의 횟수가 포아송 분포를 따를 때, 어떤 사건이 처음 발생할 때까지 걸린 시간의 확률 분포
  
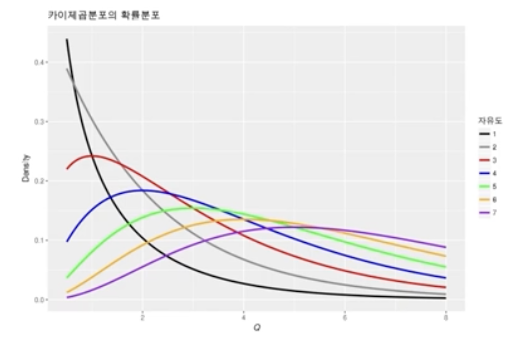
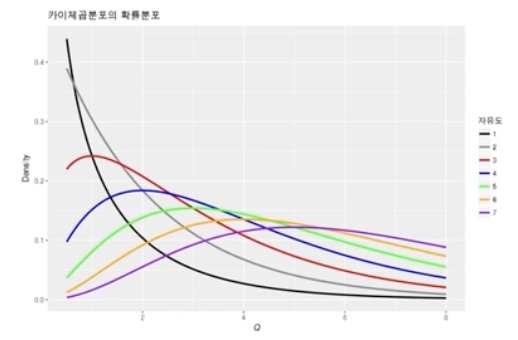
• 카이제곱 분포: 확률 변수 $z$가 표준 정규분포를 따를 때, $z^2_{1}+z^2_{2}+...+z^2_{n}$의 분포
  
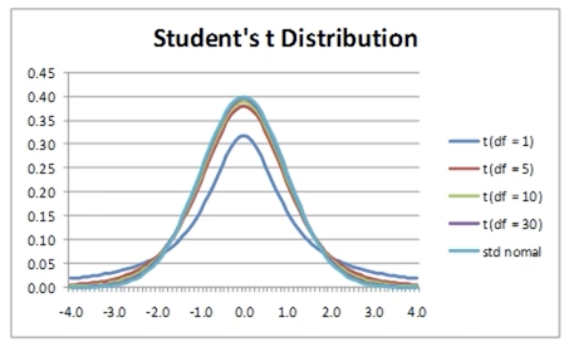
• t-분포: 표준정규분포처럼 0을 중심으로 종형의 모습을 가진 대칭 분포이나, 모분산(모표준편차)을 알 수 없는 경우에 활용 가능
  
• F-분포: 정규분포를 이루는 모집단에서 독립적으로 추출한 표본들의 분산비율이 나타내는 확률 분포

*이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다.