머신러닝 - 의사결정나무

1. 의사결정나무(Decision Tree; DT)의 개념

• 데이터를 기반으로 의사결정을 내리는 과정을 트리(Tree) 구조로 표현한 머신러닝 알고리즘
• 주로 분류(Classification)와 회귀(Regression) 문제에 사용됨
• 트리의 각 노드(Node)는 특징(feature)에 따라 데이터를 분할하고, 최종적으로 결정값(leaf node)을 반환

---

2. DT의 원리

2-1. 분할(Splitting)

• 트리는 특징(feature)을 기준으로 데이터를 반복적으로 분할하여 트리의 깊이를 늘림
• 데이터를 분할하는 기준은 불순도(Impurity)를 최소화하는 방향으로 결정됨

2-2. 불순도(Impurity)와 엔트로피(Entropy)

• 엔트로피는 불순도를 정량적으로 측정하는 척도 중 하나임
• 엔트로피가 0에 가까울 수록 데이터가 잘 분리되었음을 의미하며, 1에 가까울 수록 데이터가 잘 분리되지 않았음을 의미
  • $H(S) = -\sum_{i=1}^{n} p_i \log_2 p_i$
  • $p_i$: 클래스 $i$에 속할 확률
• A: 6개, B: 4개로 분류된 노드의 엔트로피는?
  • $H(S) = - (0.6 \cdot \log_2(0.6) + 0.4 \cdot \log_2(0.4))$
  • $H(S) \approx 0.9708$
• A: 9개, B: 1개로 분류된 노드의 엔트로피는?
  • $H(S) = - (0.9 \cdot \log_2(0.9) + 0.1 \cdot \log_2(0.1))$
  • $H(S) \approx 0.4689$
• 즉 더 낮은 엔트로피를 갖는 A: 9개, B: 1개로 분류된 노드의 분류 성능이 더욱 우수함을 의미함

2-3. 불순도(Impurity)와 지니 계수(Gini Index)

• 지니 계수는 log 계산 없이 불순도를 측정할 수 있는 방법을 나타냄
• 마찬가지로, 지니 계수가 0에 가까울 수록 데이터가 잘 분리되었음을 의미하며, 1에 가까울 수록 데이터가 잘 분리되지 않았음을 의미
  • $Gini = 1 - \sum_{i=1}^{n} p_i^2$
  • $p_i$: 클래스 $i$에 속할 확률
• A: 6개, B: 4개로 분류된 노드의 지니 계수는?
  • $Gini = 1 - (0.6^2 + 0.4^2) = 0.48$
• A: 9개, B: 1개로 분류된 노드의 지니 계수는?
  • $Gini = 1 - (0.9^2 + 0.1^2) = 0.18$

2-4. 정보 이득(Information Gain)

• 정보 이득은 주어진 데이터를 특정 Feature으로 분할했을 때, 불순도(ex. 엔트로피)가 얼마나 감소하는지를 측정하는 개념

• 정보이득이 클수록, 그 속성은 데이터 분할에 더 유용하다고 판단할 수 있음

  • $IG(S, A) = H(S) - \sum_{v \in Values(A)} \frac{|S_v|}{|S|} H(S_v)$
  • $H(S)$: 원래 데이터의 엔트로피
  • $H(S_v)$: 분할된 각 그룹의 엔트로피
  • $|S_v|/|S|$: 분할된 그룹의 비율

• 다음과 같이 분류를 수행한 DT의 엔트로피 기반 정보이득은?
  

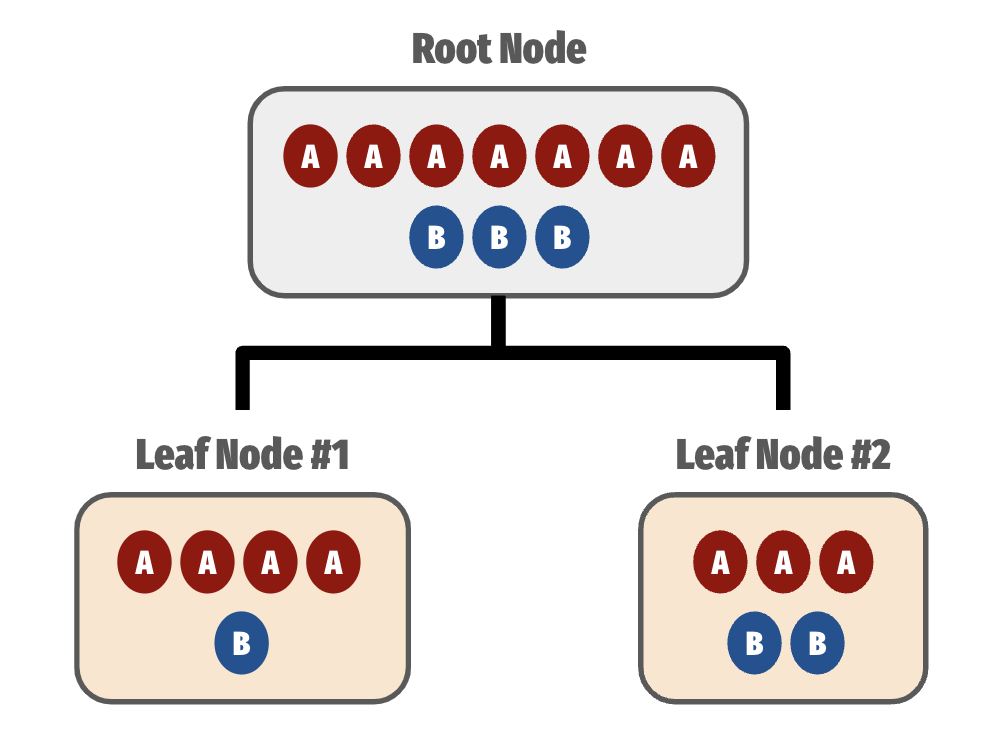
  • Root Node (Before Split):
    $H(S) = - (0.7 \cdot (-0.514) + 0.3 \cdot (-1.737)) \approx 0.863$
  • After Split:
    • Leaf Node #1:
      $H(S_X) = - (0.8 \cdot \log_2(0.8) + 0.2 \cdot \log_2(0.2)) = 0.722$
    • Leaf Node #2:
      $H(S_Y) = - (0.6 \cdot \log_2(0.6) + 0.4 \cdot \log_2(0.4)) = 0.971$
    • 가중평균:
      $\frac{5}{10} \cdot 0.722 + \frac{5}{10} \cdot 0.971 = 0.8465$
  • 정보 이득 (IG; Before Split - After Split):
    $0.863 - 0.8465 = 0.0165$

2-5. 가지치기(Pruning)

• 트리가 과도하게 성장하여 과적합(overfitting)이 발생하는 것을 방지하기 위해, 일부 가지를 제거하는 방법
  • 사전 가지치기: 트리의 성장 제한 (ex. 최대 깊이 설정)
  • 사후 가지치기: 트리 성장 후 성능 향상을 위해 가지 제거

2-6. 정지 조건

• 마찬가지로 과적합(overfitting)을 방지하고, 학습 시간을 절약하기 위해 학습을 정지시기는 조건
  • 노드에 데이터가 단일 클래스만 포함되는 경우 정지
  • 정보 이득이 특정 임계값 이하가 되는 경우 정지
  • 최대 깊이에 도달한 경우 정지 등

---

3. DT의 장단점

• 장점
  - 이해하기 쉽고 의사결정 과정을 보고 이해할 수 있음 (모델 내재적 설명력 보유)
  - 정규화(Normalization)가 불필요함
  - 데이터와 모델 간의 관계를 직관적으로 파악할 수 있음

• 단점
  - 과적합 가능성 높음
  - 데이터 변화에 민감할 수 있음

---

4. DT 기반 주요 알고리즘

• CART(Classification And Regression Tree): 이진 트리 방식으로 분류와 회귀 모두 지원
• ID3: 정보 이득(Information Gain)을 사용하여 분할 기준 결정
• C4.5: ID3의 개선 버전으로 정보 이득비(Gain Ratio)를 사용

---

5. 예시 코드: 붓꽃 분류

• Iris 데이터 로드

iris = load_iris()
X = pd.DataFrame(iris.data, columns=iris.feature_names)
y = pd.DataFrame(iris.target, columns=["target"])
data = pd.concat([X, y], axis=1)

• Pairplot 활용 시각화

sns.pairplot(data=data, hue="target")
plt.show()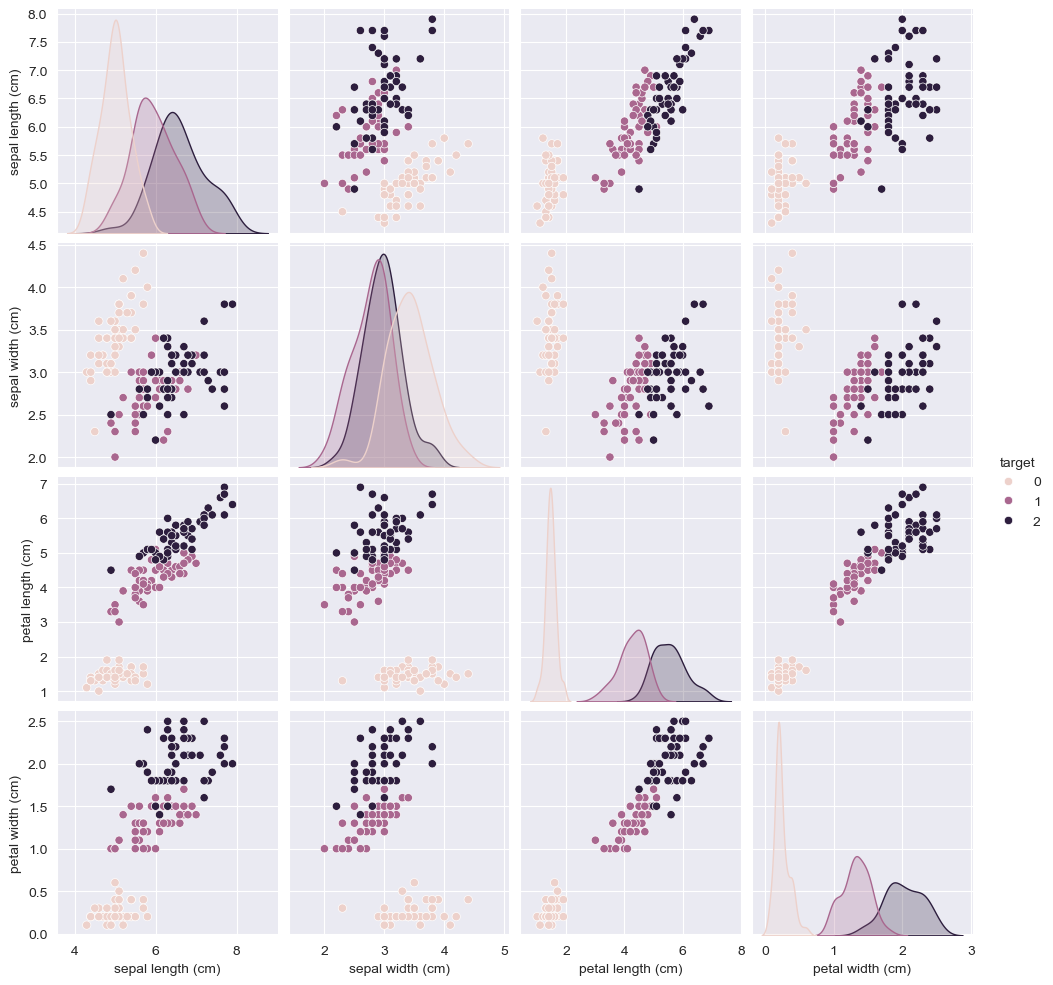

• DT모델 생성

from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import classification_report

# 데이터셋을 8:2 비율로 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 모델 훈련
dt_model = DecisionTreeClassifier(random_state=42)
dt_model.fit(X_train, y_train)

• 예측

y_pred_dt = dt_model.predict(X_test)
classification_report_result_dt = classification_report(y_test, y_pred_dt)

print(classification_report_result_dt)

## 출력 결과
#               precision    recall  f1-score   support
# 
#            0       1.00      1.00      1.00        10
#            1       1.00      1.00      1.00         9
#            2       1.00      1.00      1.00        11
# 
#     accuracy                           1.00        30
#    macro avg       1.00      1.00      1.00        30
# weighted avg       1.00      1.00      1.00        30

• 모델 시각화

from sklearn.tree import plot_tree
plt.figure(figsize=(12, 8))
plot_tree(dt_model, filled=True,
          feature_names=X.columns,
          class_names=["setosa", "versicolor", "virginica"],
          rounded=True)
plt.tight_layout()
plt.show()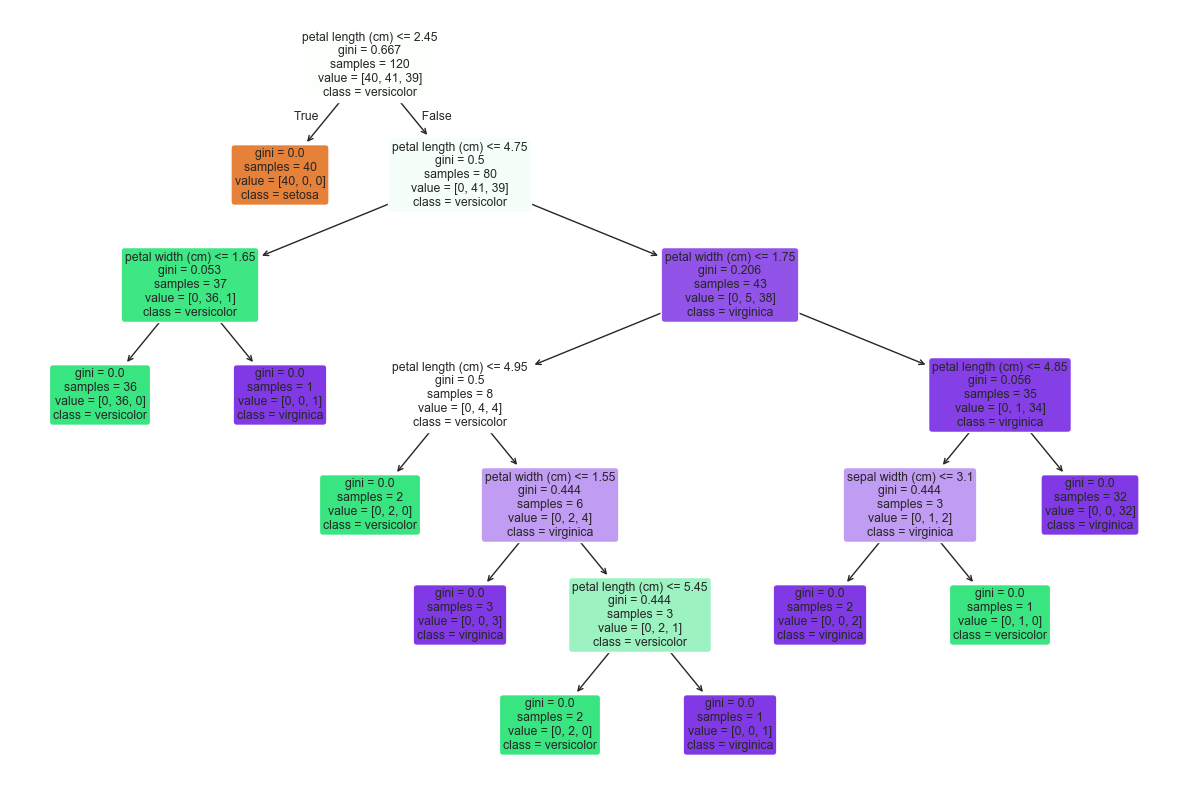

*이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다.