본 강의에서는
증명이나 자세한 설명을 하지 않고 photogrammetry에서 사용되는 수학적 성질들을 다룬다.

Topics

• $Ax = b$ 풀기
• SVD(특이값분해)를 이용하여 $Ax = 0$ 풀기
• Least squares with Gauss Newton
• Skew-symmetric matrix
• Derivative of rotation matrices
• Homogenous coordinates (다음 강의)

---

1

Linear Equation(일차방정식): $Ax = b$

세 가지 경우가 존재한다

• 유일해 (A is square matrix(정방행렬), has full rank)
• 해가 없음 (overedetermined)
• 무수히 많은 해 (underdetermined)

Solving $Ax = b$, w/ Exact Solution

유일해가 나올 조건

• A가 full rank를 갖는 정방행렬(square matrix)
• 식을 푸는 방법은 여러개 존재
  

Solving $Ax = b$, overdetermined

• real-world situation에서 일반적
• 해가 없음
• 따라서 우리의 목표는 $||Ax-b||$를 최소화 하는 것:

  $x^*$ = $argmin_x(||Ax-b||)$

• 최소제곱법(least squares) 사용
• 해(solution)은 다음과 같은 식을 통해 얻어짐

  $x = (A^TA)^{-1}A^Tb$

Solving $Ax = b$, underdetermined

• 무수히 많은 해 존재
• 충분히 많은 정보가 없는 것

  접근법: $Ax = b$의 해가 되고 $||x||$를 최소화하는 $x$를 찾는 것

• 해는 다음과 같음

  $x = A^T(AA^T)^{-1}b$

---

2

Homogeneous System(동차선형시스템) $Ax = 0$

• $Ax = 0$을 만족시키는 $x$가 0이 아닌 해를 찾는 것
• system이 underdetermined (무수히 많은 해 존재)라는 뜻
• $null(A)$라고 불리는 $A$의 null space가 존재하고,
  모든 $x$는 $Ax = 0$를 만족한다.
• $A$의 rank deficiency(차원 부족)은 null space의 dimemsionality(차원)을 정의한다.
  ex. A가 5x5 matrix인 경우, rank(A)=3이라면 null(A)=2라는 뜻

Eigenvalues(고윳값)

• 정방행렬에 대해서
  $dim(A) = dim(null(A)) + rank(A)$

  Q. 이것이 A의 eigenvalues(고윳값)에 미치는 영향이 무엇일까...?
  : $rank(A)$는 고윳값들 중 값이 0이 아닌 개수
  : $dim(null(A))$는 고윳값들 중 값이 0인 개수를 의미한다.

Eigenvector (고유벡터)

• 각각의 eigenvector인 $\nu$는 $A\nu = \lambda\nu$ 성립함
• 따라서 고윳값이 0일 경우에는 $A\nu = 0\nu = 0$

  고유값 0에 대응되는 모든 고유벡터들은 $Ax = 0$

Eigenvector & Singular Vectors(특이벡터)

• A가 정방행렬(square), 실수행렬(real), 대칭행렬(symmetric)이고 + 음수가 아닌 고윳값을 가진다면, 고윳값은 singular value(특이값)이라고 할 수 있다.
• singular vectors and values (특이벡터와 특이값)은 또한 정방행렬이 아닐 때도 존재할 수 있음
• singular vectors and values (특이벡터와 특이값)을 계산하기 위해 SVD 사용

---

3

SVD(Singular Value Decomposition)

• SVD는 행렬 A를 다음과 같이 쪼갠다
  $A = UDV^T$
  

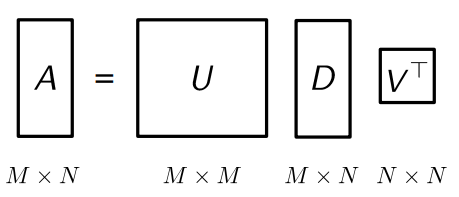
Singular Values

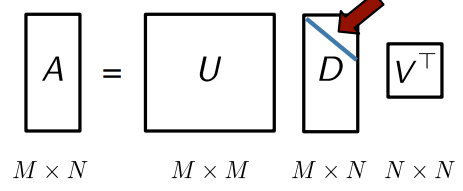
• $D$는 singular value(특이값)을 큰 것부터 작은 것 순으로 정렬한 대각행렬
• $U,V$는 orthogonal matrix(직교행렬)

Singular Vectors

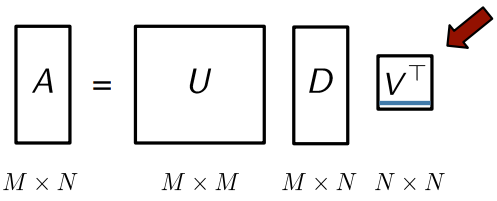
• $V^T$는 singular value(특이값)에 대응되는 singular vectors(특이벡터)를 갖고 있음
  
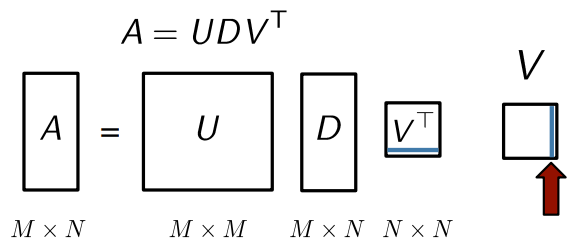
• 코딩할 때 대부분의 libraries는 $V^T$가 아니라 $V$를 반환하기 때문에 주의하기
• $V$의 마지막 열은 가장 작은 특이값에 대응하는 특이벡터를 나타냄

---

Solution to $Ax=0$ via SVD

• SVD를 이용해서 A를 분해함 : $A = UDV^T$

• D에 있는 가장 작은 특이값이 0인지 확인: $D_{NN}=0$

• 그렇다면, V의 마지막 열은 자명하지 않은 해(non-trivial solution)이다.

  자명하지 않은 해(non-trivial solution)
  : $Ax = 0$에서 $x$가 0이 아닌 해 (우리가 관심있음)

• 그렇지 않다면, 자명하지 않은 해(non-trivial solution)가 존재하지 않음 (오직 자명해만 존재)

• 그러나, V의 마지막 열은 $||x|| = 1$보다 작다는 제약 아래, $||Ax||$를 최소화할 수 있는 벡터를 나타냄

---

4

Least Squares (최소제곱법)

Graphical Explanation

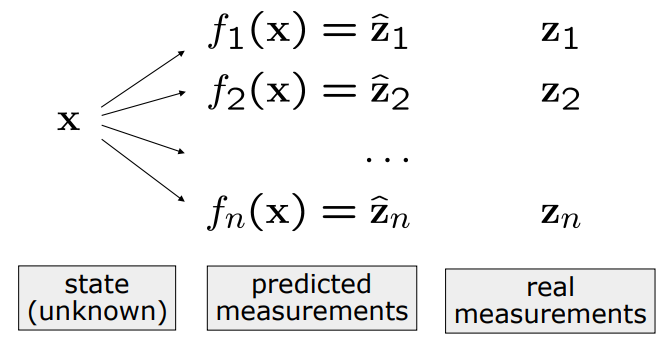
Error Function

• error $e_i$는 predicted와 actual 사이의 차이
  
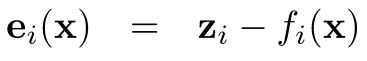
• 우리는 error가 평균이 0이고 정규분포를 따른다고 가정