[참고한 블로그]
https://junsk1016.github.io/opencv/DLT/
https://darkpgmr.tistory.com/108
https://darkpgmr.tistory.com/106
.
.
.
칼럼 주제
행렬 이 정방행렬인 경우,
인 경우,
를 어떻게 구하는가
DLT (강의 자료)
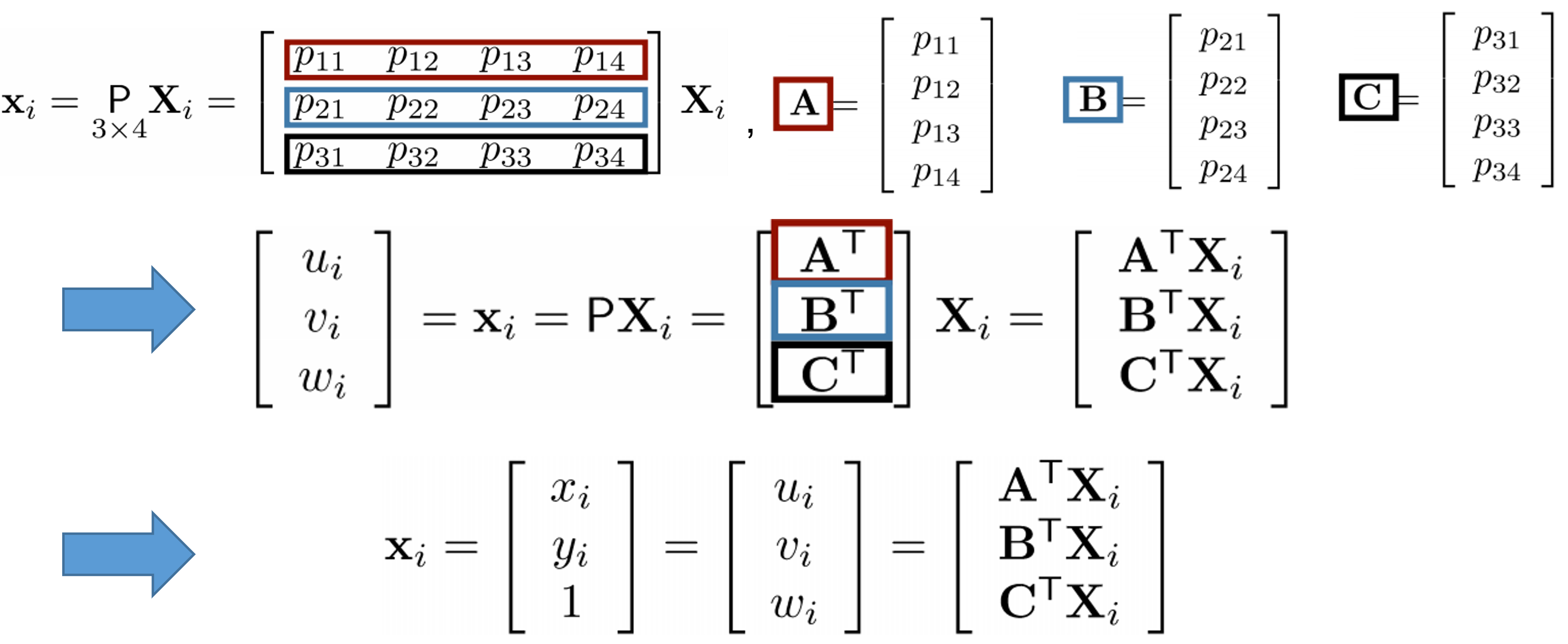
새롭게 벡터 A,B,C를 이용하여 위와 같이 표현할 수 있다.
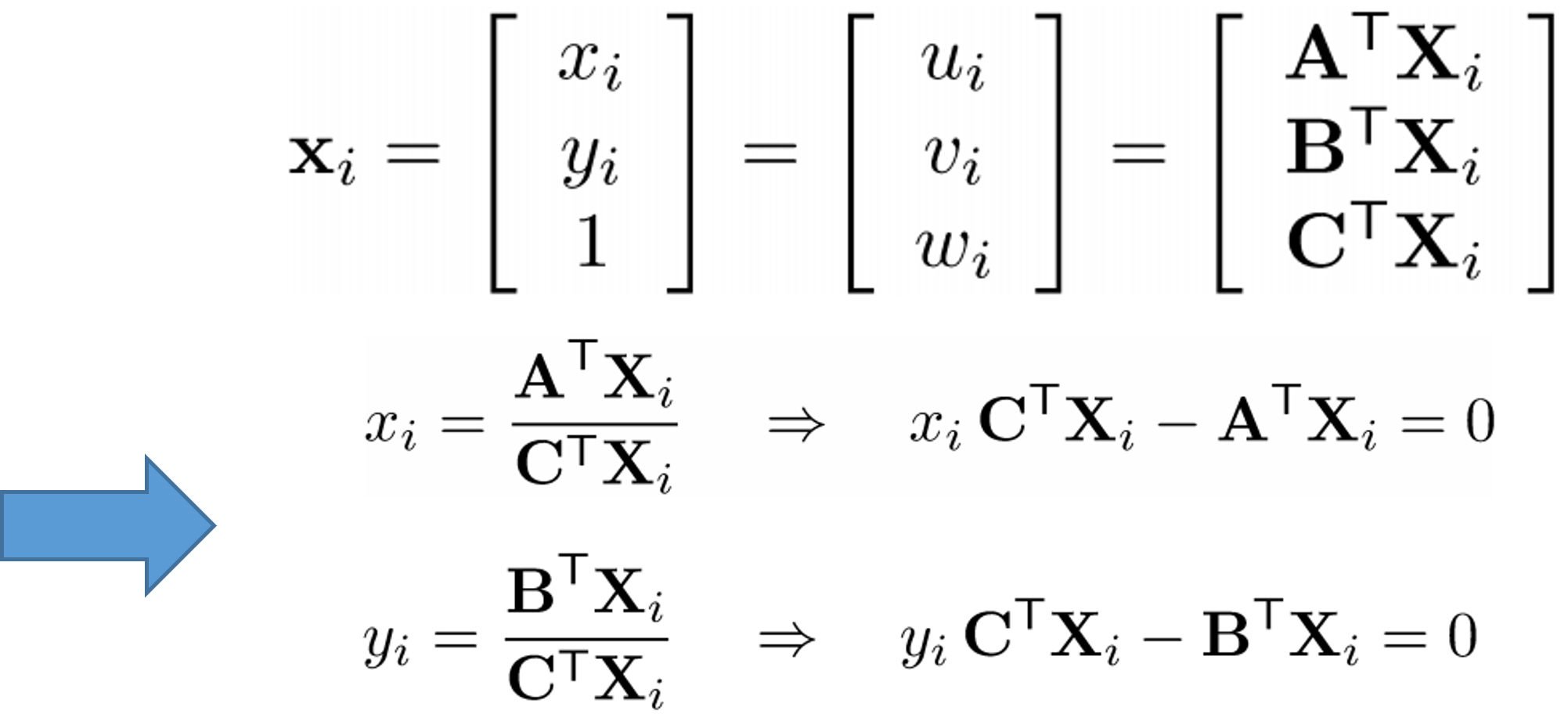
한 개의 이미지에 대한 이미지 좌표인 와 는 우리가 알고 있는 것
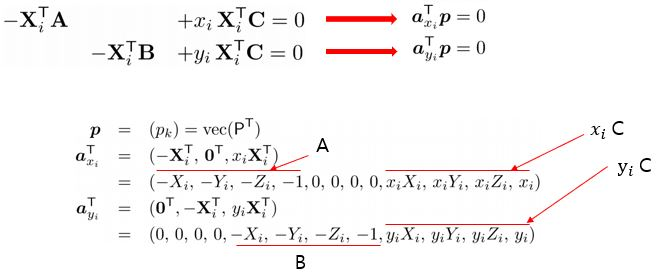
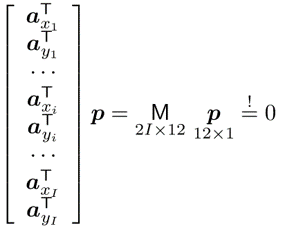
각 point에 대하여 와 를 정의할 수 있고
개의 point에 대해 한번에 쓰면 이와 같이 표현 가능!
이제 이 식을 풀면 되는 것인데
이는 선형방정식 를 푸는 것과 동일

- 를 푸는 것은 의 null space(영공간)을 찾는 것과 같다.
- 따라서 우리는 SVD(특이값 분해)를 통해서 해결할 수 있다.
- 특이값 0에 해당하는 특이벡터 를 선택하기


하지만 실제 세계이기 때문에 실제로는 이 아닌 이다.따라서, 우리의 목표는 를 최소화하는 를 구하는 것!
= M의 SVD를 구해 가장 작은 고유벡터(singular vector) 선택하는 것
= 그 고유벡터를 의 solution으로 사용하는 것
선형방정식의 풀이방법 및 SVD
- 형태일 때,
- 의 역행렬이 존재하는 경우:
- 의 역행렬이 존재하지 않는 경우:
(: 의 유사 역행렬)
- 형태일 때,
- 의 특이값분해(SVD)를 라 할 때,
는 의 가장 오른쪽 열벡터
(즉, 의 최소 특이값에 대응하는 특이벡터)
위에서 언급했듯이
우리는 => SVD =>가장 오른쪽 열벡터
특이값들이 모두 0이 아니면 -> 역행렬 존재
특이값들 중 0이 포함되면 -> 역행렬이 존재하지 x
[결론]
우리는 역행렬이 존재하는 경우를 생각하고 있으므로 특이값이 0이 나오는 경우는 발생하지 않는다.
따라서, 가장 작은 특이값은 하나만 나올 것이고 그에 대한 특이벡터를 구하면 그것이 바로 해가 되는 것...!
.
.
.
:D... 이렇게 간단한 결론이 나오는게 맞을까나..?
