[SSL Paper Review] 0. Semi-Supervised Learning Survey Paper

부스트캠프에서 마스크 정착용 이미지 분류 대회를 진행하며, 데이터 수의 부족과 클래스 불균형 문제의 근본적인 해결을 위해 외부 데이터셋을 찾아 학습에 사용할 방법을 고민했었다.

우리가 가진 원래의 데이터 셋은 사람의 성별, 나이, 마스크 정착용 여부 3가지가 레이블링되어 있었는데, 이 모든 조건이 레이블링 되어있는 외부 데이터셋은 찾을 수 없었다.

따라서 우리가 찾은 약 40만개의 데이터셋을 이용하기 위해 Self-training의 Pseudo-Labeling 기법을 사용하여 외부 데이터셋을 사용했고, 근본적인 문제를 다소 해결할 수 있었다.

이전에도 레이블링이 되어있지 않은 데이터를 활용하는 방법이 있다는 것은 알고 있었지만, 실제로 코드로 구현하여 사용해본 것은 처음이었고 굉장히 큰 재미를 느꼈다. 이 경험이 내가 Semi-Supervised Learning(SSL) 방법론에 대한 관심을 가지게 된 계기였다.

취업 후 인턴 과제로 논문 리뷰를 받았는데 그때 Soft-Teacher를 리뷰했다. 최근 논문이다 보니 SSL 학습방법론의 이전 논문의 방법을 사용했는데, 배경지식이 부족하여 논문을 읽는데에 애를 먹었다. 좀 제대로 깊게 공부해보고 싶어서 SSL survey 논문을 통해 SSL 방법론의 논문을 초기부터 쭉 리뷰해보고자 한다.
A Survey on Deep Semi-supervised Learning, IEEE 2021

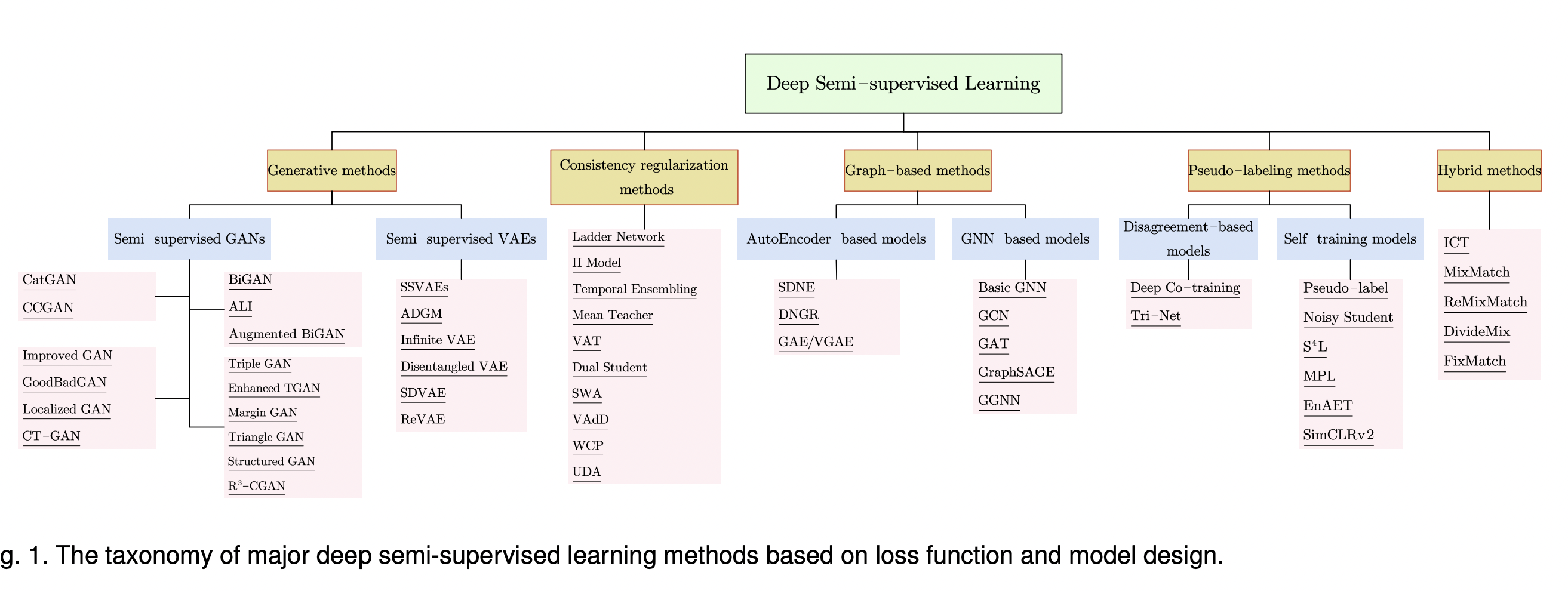
논문에서 보여주는 Deep Semi-supervised Learning의 갈래는 다음과 같다. 모든 것을 리뷰할 수 있으면 좋겠지만 현재는 배경지식의 한계로,,, Pseudo-Labeling methods, Hybrid methods, Consistency regularization methods 세가지를 리뷰할 계획이다.

또한 SSL이 기존 SL 모델의 성능을 올려줄 수 있지만, 항상 그런 것은 아니다. 레이블 되지 않은 데이터가 의미있게 사용되기 위해서는 데이터 분포에 대한 몇 가지 가정이 필요하다.
SSL의 가정은 아래와 같다.

• The smoothness assumption
  "만약 데이터 포인트가 고밀도 지역에서 가까이 위치하다면, 각걱에 연관된 레이블도 가까워야한다."

  이는 같은 class에 속하고 같은 cluster인 두 입력이 입력공간 상에서 고밀도 지역에 위치하고 있다면, 해당하는 출력도 가까워야한다는 것을 의미한다. 반대도 역시 성립하는데, 만약 두 데이터포인트가 저밀도지역에서 멀리 위치한다면, 해당하는 출력도 역시 멀어야 한다. 이러한 가정은 classification엔 도움이 되는 가정이지만 regression에선 별로 도움이 안된다.

• low-density assumption
  "모델의 결정 경계가 데이터의 확률 밀도가 높은 곳을 지나지 않는다."

  low-density 가정은 smoothness 가정과 연관성이 있는데, low-density 가정에 따라 모델의 결정 경계를 두면 low-density 지역은 그 주변에 데이터들이 적기 때문에 smoothness 가정을 위반하지 않는다. 반면에 high-density 지역에는 데이터들이 많이 모여 있을 것이고, 해당 지역에 결정 경계를 놓는다면 가까운 데이터는 같은 레이블을 가진다는 smoothness 가정을 위반하게 된다. 아래 그림은 이러한 가정들을 통해 만들어지는 결정 경계를 보여준다.
  

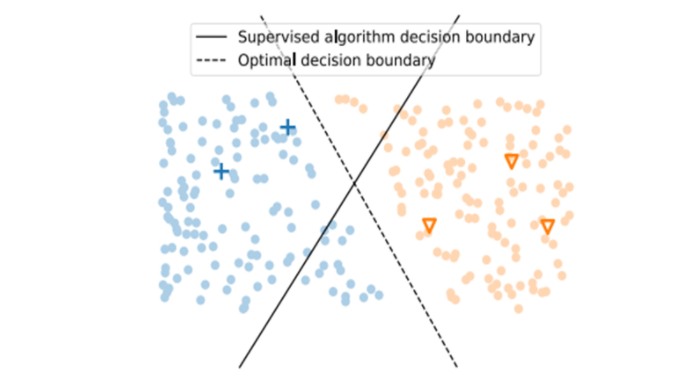
• The manifold assumption
  "고차원의 데이터를 저차원 manifold로 보낼 수 있다."

  이는 입력 데이터가 실제로는 여러 개의 저차원 manifold의 결합으로 이루어져 있다는 것과, 같은 manifold 상의 데이터는 같은 레이블을 가지고 있다는 것을 의미한다. 고차원의 공간상에서 generative task를 위한 진짜 data distribution은 추정하기 어렵다. 또한 discriminative task에서도 고차원에서는 class간의 distance가 거의 유사하기 때문에 classification이 어렵다. 그러나 만약 data를 더 낮은 차원으로 보낼 수 있다면 우리는 unlabeled data를 사용해서 저차원 표현을 얻을 수 있고 labeled data를 사용해 더 간단한 task를 풀 수 있다.
  

• The cluster assumption
  "만약에 데이터들이 같은 cluster에 있다면, 그들은 같은 class일 것이다."

  클러스터 가정은 위 가정들의 일반화로 볼 수 있는데, 이에 따르면 클러스터링을 할 때 유사도(similarity)를 기준으로 클러스터를 나눈다. 이때 입력 공간상에서 가까운 것들을 클러스터로 본다면 smoothness 가정이 되고, 확률 밀도가 높은 지역의 데이터 포인트를 클러스터로 본다면 low-density 가정이 되고, 저차원 manifold 상의 데이터 포인트들을 클러스터로 본다면 manifold 가정이 된다.

ref
A Survey on Deep Semi-supervised Learning, IEEE 2021
Semi-supervised learning (준지도학습): 개념과 방법론 톺아보기
Semi-supervised learning 방법론 소개