강의 내용 복습

(03강) Optimization

용어 정리

1. Generalization

일반적으로 train error가 작다고 해도 성능이 높다는 것을 의미하지 않는다. test data에 대해서는 성능이 안좋을 수도 있기 때문이다.
좋은 Generalization perfomance를 가지고 있다 는 것은 학습데이터만큼의 성능이 테스트데이터에서도 나온다는 것이다. 즉 Generalization Gap이 작다는 것이다.
물론 학습데이터에서 성능이 잘 나오지 않는데 Generalization Gap이 작다고 성능이 좋다고 말할 수는 없다.

2. Under fitting vs. Over fitting
이처럼 train data 에만 fit되어 test data에서는 나쁜 성능을 내는 현상을 Over fitting이라고 한다.
Under fitting은 네트워크가 너무 간단하거나 데이터가 적어 train data에서도 성능이 나쁜 현상을 말한다.

3. Cross Validation
따라서 train, validation 데이터를 나누어 학습에 사용되지 않은 validation data를 기준으로 성능이 잘 나오는지 확인한다.
그렇다면 둘의 비율을 어떻게 나누어야 할까?
validation data의 비율을 너무 크게 한다면 오히려 학습데이터의 수가 적어져 제대로 학습이 안되는 문제가 있다.

사진 출처

따라서 전체 학습데이터를 K개의 fold로 나눈 후 학습 시 에 k-1 개의 fold를 합쳐 학습데이터로, 나머지 하나의 fold를 validation data로 사용하는 방법이 있다. 만약 5개의 fold로 나누었다면 5번의 학습시 fold1부터 fold5까지 돌아가면서 validation data가 된다.
이 방법을 k-fold cross validation이라고 한다.

일반적으로 lr, loss 등의 사람이 직접 정해야하는 최적의 hyper parameter set을 찾고 찾은 hyper parameter를 고정하고 전체 train data로 학습을 시킨다. 이 전체 과정에서 test data는 절대 사용해서는 안된다.

Cross Validation : 모델의 일반화 오차에 대해 신뢰할만한 추정치를 구하기 위해 훈련,평가 데이터를 기반으로 하는 검증기법
<종류>
Holdout CV : 전체데이터를 비복원추출을 이용하여 랜덤하게 학습/평가 데이터로 나눠 검증
Random Sub-Sampling : 모집단으로부터 조사의 대상이 되는 표본을 무작위로 추출
K-Fold CV : 데이터 집합을 무작위로 동일 크기를 갖는 K개의 부분집합으로 나누고, 그중 1개를 validation data로, 나머지 집합을 학습데이터로 선정하여 모델 평가
LOOCV(Leave-One-Out CV) : 전체 데이터 N개 중 1개만을 validation data로 사용하고 나머지를 학습 데이터로 사용하는 과정을 N번 반복
LpOCV(Leave-p-Out CV) : 전체 데이터 N개 중 p개만을 validation data로 사용하고 나머지를 학습 데이터로 사용하는 과정을 $_{n}\mathrm{C}_{p}$번 반복
Bootstrap : 주어진 데이터에서 단순 랜덤 복원추출을 이용하여 동일한 크기의 표본을 여러개 생성하는 샘플링 방법

항목	LOOCV	K-Fold	Random Sub-Sampling
장점	손실되는 데이터 없음	LOOCV에 비해 측정, 평가 비용 적음	측정, 평가 비용 가장 적음
단점	측정, 평가 비용 비쌈	10-fold 사용한다면 10%의 데이터 손실(학습에 사용 못함)	미래 예측시 신뢰성 추정 불가

출처 : 2021 수제비 빅데이터분석기사 필기

4. Bias-variance tradeoff
총을 쐈을 때 항상 과녁의 같은 곳에만 집중되면 low-variance라고 한다. 즉 모델의 예측이 중구난방하지 않고 일관적이라는 것이다.
variance가 크다면 비슷한 입력이 들어와도 출력이 많이 다르고, over fitting될 확률이 크다. >왜? 데이터의 분산이 크면 모델이 각 데이터의 지엽적인 부분까지 학습하기 때문에 오버피팅 되게 된다.

반대로 bias는 비슷한 입력에 대해 (variance가 크더라도) 평균적으로 봤을 떄 true target에 접근하게되면 bias가 낮다고 말한다. bias가 크다면 내가 원하는 어떤 값에서 많이 벗어나 있는 것이다.

학습데이터에 노이즈가 끼어있다고 가정했을 때, 이 노이즈가 끼어있는 target data에서 cost를 minimize하는 것은 사실 3가지 부분으로 나누어져있다.
bias^2, variance, noise

bias를 많이 줄이게 되면 variance가 높아지고, 마찬가지로 variance를 줄이면 bias가 높아지는 trade off가 있다.

5. Bootstrapping
랜덤복원추출을 사용하여 동일한 크기의 표본을 여러개 생성하는 것. 예를 들어 100개의 data중 80개의 data를 뽑아 모델을 만들고, 그 다음 다시 80개의 data를 뽑아 또 다른 모델을 만드는 것을 반복하는 것이다. N번의 bootstrap 이후 train data sample에 한번도 포함되지 않은 data를 test에 사용한다.
이렇게 만든 여러 모델의 결과를 비교하여 불확실성을 예측할 때 사용하는 기법이다.

6. Bagging and Boosting

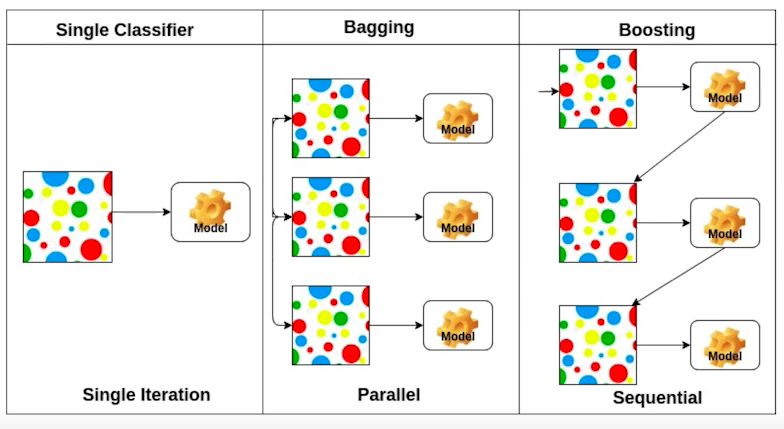
• Bagging(Bootstrapping aggregating)
  bootstraping을 이용하여 여러개의 모델을 만들고 그 결과를 평균을 낸다. 이처럼 여러 모델을 합쳐 voting을 통해 최종 결과를 내는 것을 Ensanble(앙상블)이라고 한다.

• Boosting
  weak learner들은 sequetial 하게 합쳐 하나의 strong leaner를 만드는 방법.
  예를 들어 첫번째 만든 모델이 80개의 data에 대해서는 예측을 잘하지만 20개의 data에 대해서는 성능이 좋지 않을 때, 그 20개의 data를 잘 예측하도록 두번째 모델을 만든다. 이를 반복하여 만든 weak leaner들의 weight를 찾아 취합하는 것을 Boosting이라고 한다.

Ensanble(앙상블)
<특징>
다양한 모델의 예측결과를 결합함으로써 단일모형으로 분석했을 때보다 높은 신뢰성
이상값에 대한 대응력이 높아지고 전체 분사이 감소하여 정확도 상승
모형의 투명성이 떨어지게 되어 현상의 원인 분석에는 부적합
<앙상블 기법의 종류>

<각 알고리즘의 특징 및 적용방안>

항목	Bagging	Boosting	Random Forest
장점	일반적으로 성능향상에 효과적이며 결측값이 존재할 때 강함	일반적으로 과대적합 없음	수천개의 변수를 제거없이 실행하므로 정확도 좋음
단점	계산 복잡도 높음	계산 복잡도 높음	이론적 설명 및 최종 결과 해석 어려움
적용 방안	소량의 데이터, 목표변수와 입력변수의 크기가 작아 단순할수록 유리	대용량 데이터, 데이터와 데이터 간 속성이 복잡할 수록 유리	입력변수가 많은 경우 유리

출처 : 2021 수제비 빅데이터분석기사 필기

Gradient Desent Methods

• Stochastic GD
  하나의 sample을 이용하여 gradient를 업데이트하는 방법

• Mini-batch GD
  data의 subset을 이용하여 gradient를 업데이트하는 방법, 대부분의 DL이 사용한다.

• Batch GD
  전체 data를 이용하여 gradient를 업데이트하는 방법

  Batch size는 중요한 hyper parameter.
  이에 대한 논문 - On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima
  Batch size를 작게 하는 것이 일반적으로 더 좋은 Generalization perfomance를 가진다는 것을 실험적으로 보이고, large batch size를 사용하기 위한 방법을 제시한다.
  -> Sharp Minima에 도달하는 것 보다는 Flat Minima에 도달하는 것이 더 좋다.
  
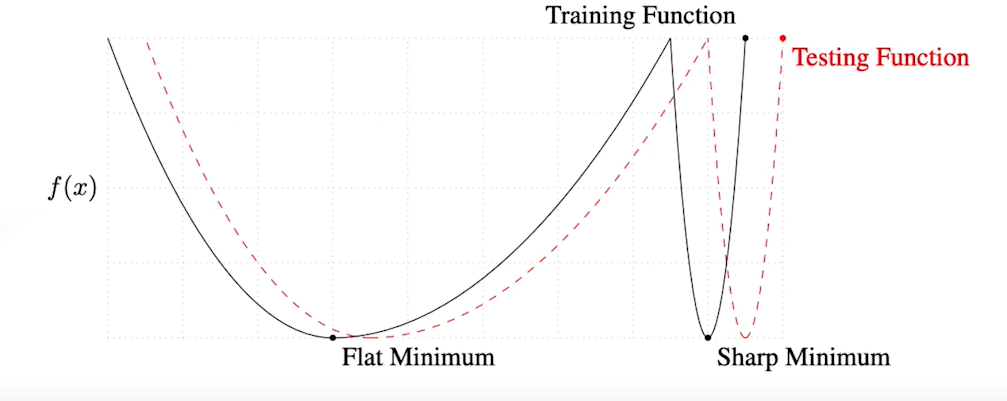
  우리의 목적은 testing function이 잘 작동하는 것이다. Flat Minima의 경우 train 에서 찾은 global minimum과 좀 멀어져도 비슷한 성능을 내지만, Sharp Minima의 경우 train 에서 찾은 global minimum과 멀어지면 testing function이 높은 값을 갖는다. 즉 train 에서 찾은 값들이 한번도 만나지 않은 test data에서는 잘 작동하지 않는다는 것이다.
  

Optimizer

1. (Stochastic) gradient descent
   
   단점 : learning rate의 적절한 값을 찾는 것이 어렵다.

2. Momentum
   
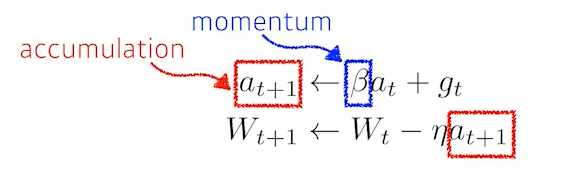
   SGD의 문제점을 해결하기 위해 gradient의 방향(momentum)을 기억하여 다음 update에 반영하는 방법. 이 방법의 장점은 한번 흘러간 gradient를 유지시켜주기 때문에 gradient가 굉장히 많이 왔다갔다 해도 학습이 잘 된다.

3. Nesterov Accelerate
   
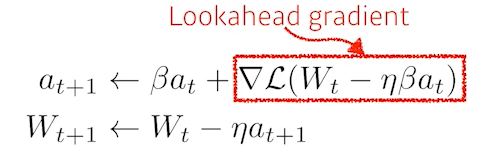
   gradient 계산 시 lookahead gradient를 계산한다. Momentum은 현재 주어진 정보에서 gradient를 계산했지만 Nesterov Accelerate는 gradient 방향으로 한번 이동하여 gradient를 계산한다.
   
   momentum은 local minimum을 converging하지 못하는 현상이 있는 반면 Nesterov Accelerate는 그 문제를 해결하여 빠르게 local minimum에 도달한다.

4. Adagrad
   
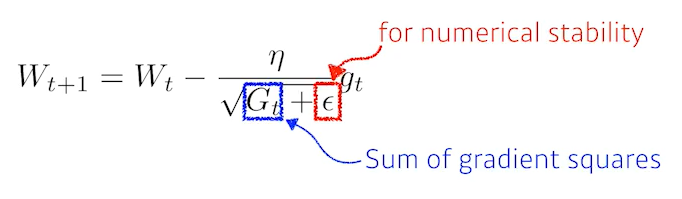
   지금까지 grdient가 얼마나 변했는지 제곱해서 더한 값(G)을 저장한다. 해당 변수는 계속 커지게 될것이고, 많이 커졌다는 것은 paramter가 많이 변했다는 것이므로 역수를 취하여 많이 변한 parameter에 대해서는 적게 변화시키고, 적게 변한 parmeter에 대해서는 많이 변화시킨다.

   단점 : G가 계속 커지기 때문에 뒤로 가면갈수록 분모가 무한대가 되어 학습이 제대로 되지 않는다.

5. Adadelta
   
   Adagrad에서 G가 계속 커지는 것을 해결하는 방법. accumulation window, 즉 전체 시간을 보는 것이 아닌 현재 timestamp t로부터 일정 window에 해당하는 시간만 보는 것이다.
   단점 : window 사이즈에 해당하는 시간만큼의 G를 저장해놓아야 한다.

6. RMSprop
   
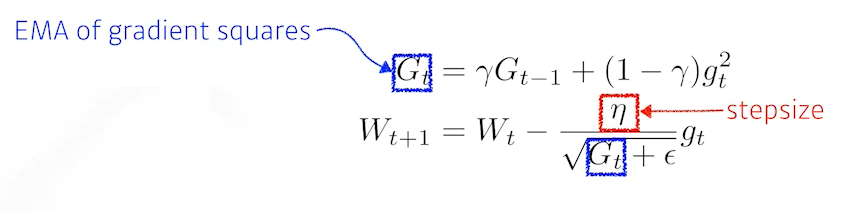
   AdaDelta의 G를 역수에 넣고 learning rate를 추가한다.

7. Adam
   
   이전의 gradient 정보인 mometum과 Gradient squares 의 크기에 따라 adaptive 하게 learning rate을 바꾸는 것을 합친 방법.
   beta1 : momentum을 얼마나 유지시킬지
   beta2 : Gradient squares에 대한 ema정보
   

잘 정리 : https://ganghee-lee.tistory.com/24

http://shuuki4.github.io/deep%20learning/2016/05/20/Gradient-Descent-Algorithm-Overview.html

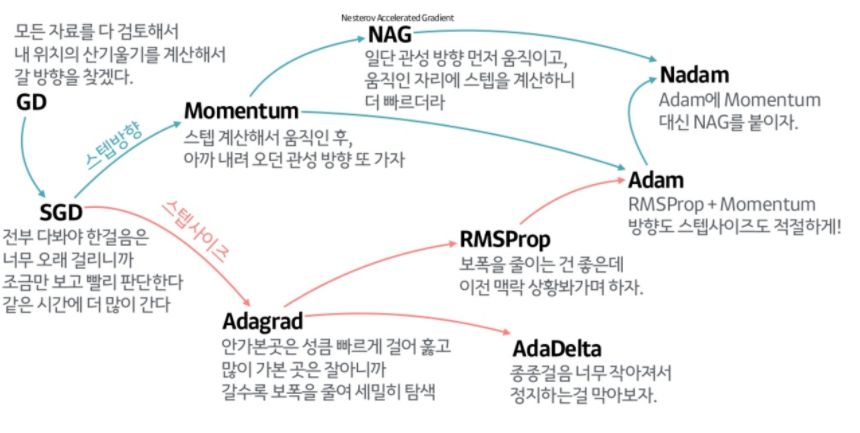
사진출처

Regularization

학습을 방해하여 test data에도 잘 동작할 수 있게 하는 것.
1. Early Stopping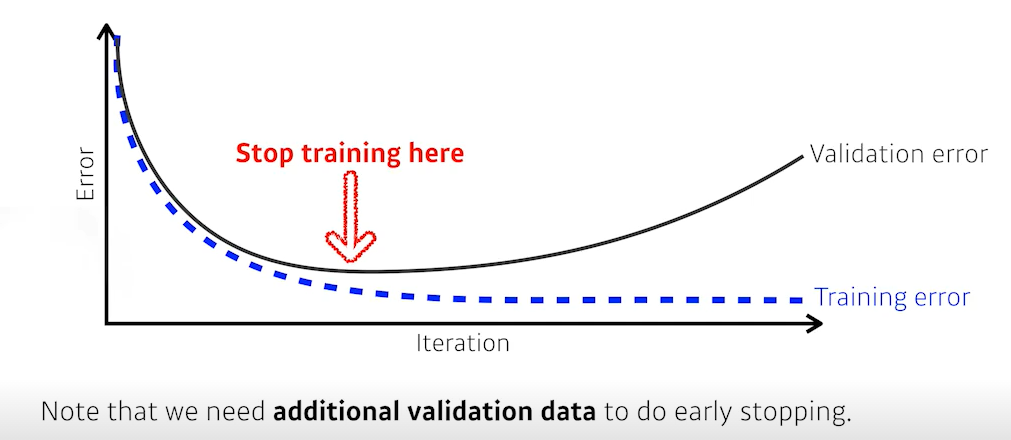
일반적으로 train error가 줄어들면 test error가 커진다. 이를 방지하기 위해 validation error가 커지면 학습을 빨리 멈추는 방법이다.

2. Parameter norm penalty(weight decay)
   네트워크의 parameter를 모두 더한 다음 제곱하여 그 숫자를 같이 줄여서 paramter가 너무 커지지 않도록 한다.

3. Data augmentation
   
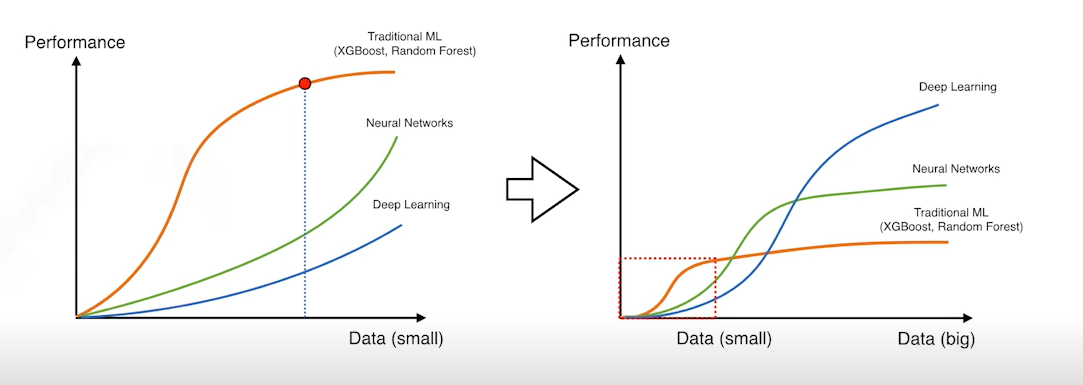
   deep learning이 잘 되려면 data는 많아야한다.
   
   실제로는 data가 충분하지 않기 때문에 가지고 있는 데이터를 label이 바뀌지 않는 선에서 변형하여 (label preserving augmentation) 데이터 갯수를 늘리는 방법.

4. Noise robustness
   
   입력데이터와 neural network의 weight에 noise를 집어넣어 성능을 높인다. (실험적인 결과)

5. Label smoothing
   
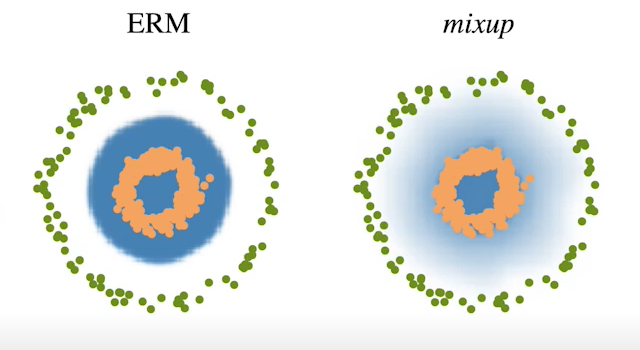
   train data 두개를 뽑아 섞어주는 것.
   분류 모델의 목적은 decision boundary를 찾는것인데, 이 boundary를 부드럽게 만들어준다.

6. Dropout
   
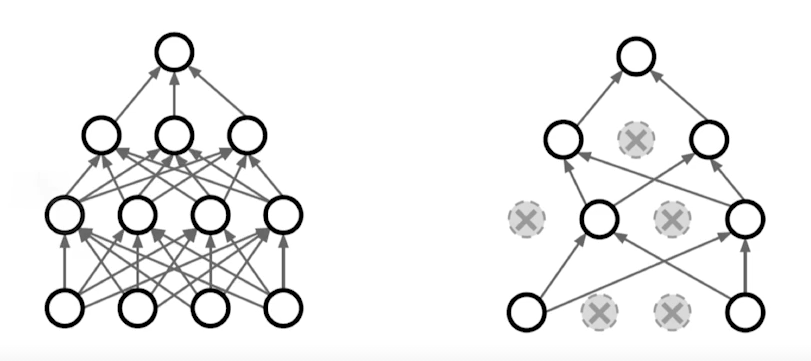
   학습시 일정 비율의 neuron을 0으로 만들어 각각의 neuron이 조금 더 robust한 특징을 잡도록 한다.(해석)

7. Batch normalization
   내가 적용하고자 하는 layer의 statistic를 정규화(평균을 빼고 표준편차로 나눠줌)하여 값을 줄여주는 방법.
   
   비슷한 다양한 방법이 있다.

---

과제 수행 과정 및 결과

• optimzer에 따른 최적화 과정, 속도 비교 및 관찰

---

피어 세션

• Bias-Variance Tradeoff에서 Variance가 크면 overfitting이 크다고 하는데 그 이유는 무엇일까요?

• Nesterov Accelerated Gradient 의 벡터 이동 그림에서 lookahead 그레디언트가 구성되는 방식에 대한 질문

• 정규분포의 모수추정에서 확률밀도함수에 x값을 넣은 것이 가능도가 되는지 의문이라는 어제(8/9) 질문에서 답변
  가능도함수와 확률밀도함수는 각각 모수를 변수로 볼 것이냐, 확률변수를 변수로 볼 것이냐만 다를 뿐
  동일한 대상입니다. (물론 식의 형태만 같을 뿐, 변수가 다르기 때문에 그래프의 모양이 같다는 말은 아닙니다!)
  TODO 4에서 case가 모평균(모수)가 -1, 0, 1일 때 각각의 경우에 대해 특정 x값이 갖게되는 '가능도'를 비교하게 됩니다.
  말씀하신 내용이 전체적으로 맞으나 bold체에 대해서만 약간의 수정이 필요할 것 같습니다.
  즉, 해당 데이터가 특정구간에 속할 확률이 아니라 특정 값을 가질 가능도라고 보시면 됩니다.
  다만 그 가능도라는 값을 pdf(확률밀도함수)를 통해 구하는 것 뿐이죠.

---

학습 회고

keep

• 헷갈리거나 추가설명이 필요한 부분 더 검색해서 찾기

problem

• 코어시간 끝나고 난 후 해야 할 일 미룸

try

• 코어시간 외에 to-do list 및 시간계획 작성해서 시간관리 필요