Nonlinear Regression

dwlee·2022년 11월 11일

Deep Learning Basics with PyTorch

목록 보기

3/7

개요

이전 포스트에서는 PyTorch를 이용하여 linear regression을 구현하였다. Linear regression에서는 데이터의 분포가 선형적인 분포를 보일 때 이를 regression하기 위한 모델은 일차함수의 형식을 가졌다. 그러나 데이터의 분포가 선형적이지 않을 때는 어떤 형식의 모델로 regression 할 것인가? 비선형적인 모델은 일차함수를 제외한 어떠한 함수도 가능하기 때문에 모델을 선택하기 쉽지 않다. 하지만 PyTorch에서는 간단한 모델로도 regression을 할 수 있다. 어떻게 하면 비선형적인 분포를 보이는 데이터에 대해 nonlinear regression을 할 수 있는지 알아보자.

1. Multi Layers

데이터가 다음 그래프와 같이 분포되어 있다고 하자.

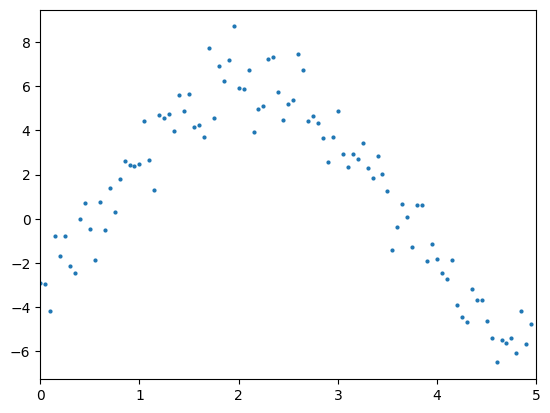
이전 포스트에서와 같이 PyTorch로 선형 모델을 만들어서 학습시켜 보자.

x = torch.arange(0, 5, 0.05).unsqueeze(1)
y = 5 * torch.sin(x) - 3 * torch.cos(x) + torch.randn(100, 1)
plt.xlim([0, 5])
plt.plot(x, y, 'o', markersize=2)
plt.show()

model = nn.Linear(in_features=1, out_features=1)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
epochs = 100

model.train()
for epoch in range(epochs):
    y_pred = model(x)

    loss = nn.functional.mse_loss(y, y_pred)

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    weight = model.get_parameter('weight')
    bias = model.get_parameter('bias')

    print(f'Loss: {loss:.3f}, weight: {float(weight):.6f},
    		bias: {float(bias):.6f} | Epoch: {epoch + 1}')

plt.xlim([0, 5])
plt.plot(x, y, 'o', markersize=2)
plt.plot(x, y_pred.detach())
plt.show()

>> Loss: 16.648, weight: -0.226444, bias: 0.151628 | Epoch: 1
Loss: 16.221, weight: -0.179475, bias: 0.183582 | Epoch: 2
Loss: 15.925, weight: -0.141800, bias: 0.212573 | Epoch: 3
...
Loss: 13.657, weight: -0.319215, bias: 1.471764 | Epoch: 97
Loss: 13.645, weight: -0.322363, bias: 1.481908 | Epoch: 98
Loss: 13.634, weight: -0.325496, bias: 1.492005 | Epoch: 99
Loss: 13.623, weight: -0.328614, bias: 1.502055 | Epoch: 100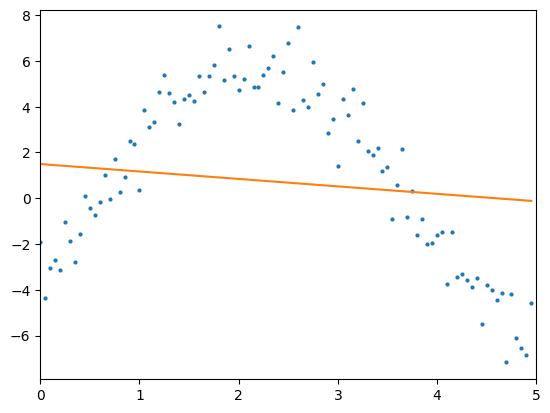

결과를 살펴보니 학습을 반복하여도 loss 값이 1보다 여전히 크고, regression 결과도 매우 부정확하다.
더 정확한 regression 결과를 얻기 위해 우선 기존 모델에 nn.Linear layer를 하나 더 추가해보자. 두 개 이상의 layer를 하나의 모델로 결합하기 위해 nn.Sequential 클래스를 사용할 수 있다.

model = nn.Sequential(
			nn.Linear(in_features=1, out_features=1),
            nn.Linear(in_features=1, out_features=1)
		)

>> Loss: 15.540 | Epoch: 1
Loss: 15.081 | Epoch: 2
Loss: 14.818 | Epoch: 3
Loss: 14.651 | Epoch: 4
...
Loss: 11.625 | Epoch: 97
Loss: 11.618 | Epoch: 98
Loss: 11.610 | Epoch: 99
Loss: 11.604 | Epoch: 100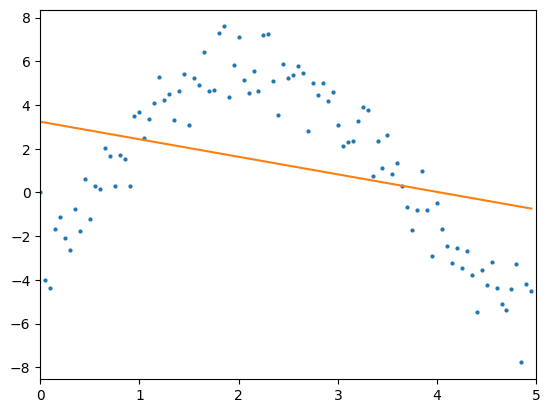

layer가 하나 더 추가되었음에도 불구하고 regression 결과가 크게 개선되지 않았다. 이러한 결과가 발생하는 이유는 무엇일까?

이전 포스트에서 언급했듯이 선형 모델은 $\hat{y} = wx+b$ 로 나타낼 수 있다. 위 예시처럼 두 개의 선형 모델이 결합되어 있으면 매개변수 값이 서로 다른 두 모델은 다음과 같이 표현할 수 있다.

$\hat{y_1} = w_1 x_1 + b_1, \hat{y_2} = w_2 x_2 + b_2$

위 예시에서는 첫 번째 layer의 출력값이 두 번째 layer의 입력값이 되므로 $\hat{y_1} = x_2$ 라 할 수 있다. 그러면 위 수식을 하나의 식으로 표현할 수 있다.

$\hat{y_2} = w_2(w_1 x_1 + b_1) + b_2 = w_2 w_1 x_1 + w_2 b_1 + b_2$

이 때, $w_2 w_1 = w_3$ , $w_2 b_1 + b_2 = b_3$ 이라 하면 $\hat{y_2} = w_3 x_1 + b_3$ 이므로 두 개의 layer가 결합된 모델도 또다른 선형 모델이라고 할 수 있다.
따라서 nn.Linear layer만 계속 추가한다고 해서 선형 모델이 비선형 모델로 바뀌지는 않기 때문에 다른 layer를 추가해야 한다. 어떤 layer를 추가할지 알아보자.

2. Activation function

Activation function은 선형 모델을 비선형 모델로 바꾸기 위해 사용하는 함수다. 선형 모델의 출력 데이터는 선형성을 가지기 때문에 그 결과에 activation function을 적용하면 비선형적인 분포를 보이게 된다. 따라서 activation function은 비선형 함수이다.

1) List of activation functions

(1) Sigmoid, Hyperbolic Tangent

Sigmoid activation function은 다음 수식으로 정의한다.

$f(x) = \cfrac{1}{1+e^{-x}}$

Sigmoid 함수는 모든 입력값에 대해 유한한 출력값을 갖고 음이 아닌 미분값을 가지기 때문에 딥러닝 초창기에 activation function으로 자주 사용되었다.
Sigmoid 함수와 모양은 비슷하나 최대/최소값이 다른 hyperbolic tangent ( $\tanh$ ) 함수도 있다.

(2) ReLU, Leaky ReLU, SiLU, GeLU

ReLU activation function은 다음 수식으로 정의한다.

$f(x) = \max(0, x)$

ReLU 함수는 입력값이 0보다 크면 그 값이 그대로 출력되고, 반대로 0이하면 출력값은 무조건 0인 특징을 갖는다. Leaky ReLU, SiLU, GeLU는 음의 입력값에서 출력값이 0이 되는 ReLU의 단점을 보완하기 위해 변형된 함수로, 음의 입력값에서도 0이 아닌 출력값을 가지는 특징이 있다.
ReLU 함수는 현재 대부분의 딥러닝 모델에서 많이 사용되는 activation 함수 중 하나다. 어떤 점에서 ReLU 함수가 activation 함수로 많이 사용되는지 알아보자.

2) Back Propagation of Nonlinear model

두 개의 linear layer 중간에 activation 함수가 결합된 nonlinear 모델에서 gradient descent로 매개변수를 업데이트하는 과정을 살펴보자.
먼저 첫번째 linear layer를 $\hat{y_i}=w_1 x_i + b_1$ , activation 함수를 $a_i=f(\hat{y_i})$ , 두번째 linear layer를 $\hat{z_i} = w_2 a_i + b_2$ 라 할 때, 이 nonlinear 모델 및 loss function은 다음 수식으로 표현할 수 있다.

$\hat{z_i} = w_2 f(\hat{y_i}) + b_2 = w_2 f(w_1 x_i + b_1) + b_2, L = \cfrac{1}{n}\sum_{i=1}^n \left(z_i - \hat{z_i} \right)^2$

그러면 gradient descent를 적용하기 위해 loss function $L$ 을 매개변수 $w$ 와 $b$ 에 대해 각각 미분해보자. 그러면 이 nonlinear 모델은 activation 함수와 일차함수의 합성함수이므로 매개변수 $w_1$ 와 $b_1$ 에 대한 도함수는 연쇄법칙에 따라 다음과 같이 표현 가능하다.

$\cfrac{\partial{L}}{\partial{w_1}} = \cfrac{\partial{L}}{\partial{\hat{z_i}}} \cfrac{\partial{\hat{z_i}}}{\partial{w_1}} = \cfrac{\partial{L}}{\partial{\hat{z_i}}} \cfrac{\partial{\hat{z_i}}}{\partial{a_i}} \cfrac{\partial{a_i}}{\partial{w_1}} = \cfrac{\partial{L}}{\partial{\hat{z_i}}} \cfrac{\partial{\hat{z_i}}}{\partial{a_i}} \cfrac{\partial{a_i}}{\partial{\hat{y_i}}} \cfrac{\partial{\hat{y_i}}}{\partial{w_1}}$

$= \cfrac{1}{n} \sum_{i=1}^n 2(\hat{z_i}-z_i) w_2f'(\hat{y_i})x_i$
$= \cfrac{1}{n} \sum_{i=1}^n 2 \left(w_2f(w_1 x_i + b_1)-z_i \right) w_2 f'(w_1x_i + b_1)x_i,$
$\cfrac{\partial{L}}{\partial{b_1}} = \cfrac{\partial{L}}{\partial{\hat{z_i}}} \cfrac{\partial{\hat{z_i}}}{\partial{b_1}} = \cfrac{\partial{L}}{\partial{\hat{z_i}}} \cfrac{\partial{\hat{z_i}}}{\partial{a_i}} \cfrac{\partial{a_i}}{\partial{b_1}} = \cfrac{\partial{L}}{\partial{\hat{z_i}}} \cfrac{\partial{\hat{z_i}}}{\partial{a_i}} \cfrac{\partial{a_i}}{\partial{\hat{y_i}}} \cfrac{\partial{\hat{y_i}}}{\partial{b_1}}$

$= \cfrac{1}{n} \sum_{i=1}^n 2(\hat{z_i}-z_i) w_2f'(\hat{y_i})$
$= \cfrac{1}{n} \sum_{i=1}^n 2 \left(w_2f(w_1 x_i + b_1)-z_i \right) w_2 f'(w_1x_i + b_1)$

이후의 gradient descent 과정은 이전 포스트와 동일하게 진행한다.

$\hat{w_1}=w_1-\alpha\cfrac{\partial{L}}{\partial{w_1}}, \hat{b_1}=b_1-\alpha\cfrac{\partial{L}}{\partial{b_1}}, L = \cfrac{1}{n}\sum_{i=1}^n \left(\hat{z_i} - z_i \right)^2$

3) Vanishing Gradient Problem

Vanishing gradient problem이란 gradient descent 적용 시 gradient 값이 0이거나 0에 가까운 값이 계산되어 매개변수가 더 이상 업데이트되지 않는 문제를 말한다. 즉, 각 매개변수에 대한 loss function의 미분값이 0에 가까운 값이 나올 때 이 문제가 발생한다고 생각할 수 있다.
2)절에서 제시한 nonlinear 모델을 예시로 들어보자. 만약 $\cfrac{\partial{L}}{\partial{w_1}}$ 과 $\cfrac{\partial{L}}{\partial{b_1}}$ 이 모두 0이라면 vanishing gradient 문제가 발생할 수 있다. 그러면 gradient가 0이 되는 경우를 살펴보자.

Case 1. $\hat{z_i} - z_i = 0$
Case 2. $w_2 = 0$
Case 3. $f'(\hat{y_i})=0$
Case 4. $x_i = 0$

Case 1은 큰 문제가 되지 않는다. 왜냐하면 $\hat{z_i} = z_i$ 의 의미는 모델의 출력값이 실제 데이터의 출력값과 일치한다는 뜻이기 때문이다. 즉, 모델 학습이 잘 되고 있는 중이라고 생각할 수 있다.
Case 2와 Case 4는 본 예시의 전제 조건과 일치하지 않는다. Case 2에서 $w_2 = 0$ 이면 두 번째 layer의 모델은 $z_i = b_2$ 인 nonlinear layer가 된다. 그리고 실제 데이터의 모든 입력값 $x_i$ 는 0이 아니므로 두 case 모두 발생할 수 없다.
그러면 유력한 조건은 Case 3인 $f'(\hat{y_i})=0$ , 즉 activation 함수의 미분값이 0이 되는 것이다. Activation 함수의 종류에 따라 그 미분값이 0이 될 수 있는데, sigmoid 함수가 이에 해당한다. Sigmoid 함수의 그래프를 살펴보자.