개요

이전 포스트에서 vanishing gradient 문제가 발생하는 이유에 대해 알아보았다. 그러면 이 문제를 해결할 수 있는 대표적인 방법에 대해 살펴보자.

1. Other activation functions

Vanishing gradient 문제는 activation 함수가 sigmoid 함수일 때 많이 발생한다. Sigmoid 함수는 입력값이 특정 범위를 벗어날 때 미분값이 0이 된다. 따라서 양의 입력값에서 미분값이 0이 되지 않는 ReLU나 SiLU, GeLU등의 함수를 activation 함수로 사용하면 vanishing gradient 문제를 줄일 수 있다.

2. Batch Normalization (BN)

Batch normalization은 batch 단위로 학습을 하는 과정에서 각 batch 별로 평균과 분산으로 normalization하는 과정을 말한다. 일반적으로 학습 속도를 높이기 위해 학습 데이터를 여러 개의 batch로 나누어서 학습을 하게 되는데, 그러면 각 batch 별로 데이터의 분포가 상이할 수 있다. 그리고 layer를 하나씩 거치면서 데이터의 분포가 달라질 수 있다. 이와 같이 layer를 거치면서 입력 데이터의 분포가 달라지는 현상을 internal covariance shift라고 하는데, 이를 해결하기 위한 방법이 바로 batch normalization이다. 그러나 batch normalization은 학습과 테스트(추론) 단계에서 적용 방법이 약간 상이한데, 어떤 차이점이 있는지 살펴보자.

1) BN in Training

Batch normalization에서는 평균이 0, 표준편차가 1이 되는 정규분포를 따르도록 데이터의 분포를 조정한다. 이 과정을 수식으로 나타내보자.

$BN(X)=\gamma \left(\cfrac{X-\mu_{batch}}{\sigma_{batch}} \right) + \beta,$
$\mu_{batch}=\cfrac{1}{B}\sum_i x_i, \sigma_{batch}^2 = \cfrac{1}{B}\sum_i \left(x_i - \mu_{batch} \right)^2$

여기서 $B$는 batch 크기, $\mu_{batch}$, $\sigma_{batch}$는 각 batch의 평균과 표준편차, $\gamma$와 $\beta$는 scaling factor이다.
먼저 학습 데이터를 정규화하는 이유를 생각해보자. 데이터를 정규화하면 모든 데이터 샘플이 같은 범위 내로 scaling 된다. 그러면 gradient descent 과정에서 local minima 지점에 빠져 학습이 중단되거나 모델의 매개변수 값이 너무 크게 변하여 최적점을 찾지 못하는 현상을 최소화할 수 있다. 즉, 데이터의 분포에 따라 매개변수가 급격하게 변하는 현상을 방지하여 최적점에 안정적으로 수렴할 수 있도록 한다.
그러나 batch normalization에서는 정규화 과정에 더하여 scaling factor가 추가되는데, 여기서 scaling factor는 무슨 역할을 하는 것일까?
사실 $\gamma$와 $\beta$가 각각 1, 0이면 일반적인 normalization 과정과 동일하다. 즉, 평균이 0, 표준편차가 1인 정규분포로 정규화된다. 그런데 이렇게 정규화된 데이터에 ReLU 함수를 activation 함수로 적용해버리면 음수인 입력 데이터는 출력값이 모두 0이 된다. 결국 전체 입력 데이터 중 절반 정도는 의미가 없어져 버리기 때문에 scaling factor를 적용하여 출력 데이터가 0이 되는 것을 방지한다.

2) BN in Inference

이제 테스트 단계에서의 batch normalization 과정을 살펴보자. 먼저 이 과정을 수식으로 나타내보자.

$BN(X)=\gamma\left(\cfrac{X-\mu_{BN}}{\sigma_{BN}} \right) + \beta,$
$\mu_{BN} = \cfrac{1}{N} \sum_i \mu_{batch}^i, \sigma_{BN}^2 = \cfrac{1}{N} \sum_i\sigma_{batch}^i$

테스트 단계에서의 정규화에 사용되는 평균과 표준편차는 학습 단계에서의 평균과 표준편차와는 다르다. 테스트 단계에서는 학습 단계에서 구한 각 batch 별 평균과 표준편차 중 최근 $N$개의 batch의 평균과 표준편차에 대한 평균값을 산출한다.

3. Residual Networks

Residual network는 이미지 분류에 많이 사용되는 모델인 ResNet의 일부분을 말한다. ResNet은 단순히 layer를 많이 쌓는 것이 아니라 아래 그림과 같이 layer 중간에 그 다음 layer로 건너뛸 수 있는 연결 구조를 갖고 있다.
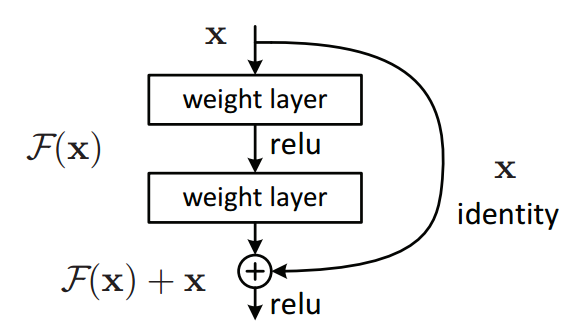출처: https://arxiv.org/abs/1512.03385

이러한 residual connection은 layer가 너무 많을 때 vanishing gradient 문제로 학습이 잘 되지 않는 문제를 해결했다. ResNet의 구조에 대한 자세한 설명은 추후 포스트에서 소개한다.

4. Weight Initialization

학습 초기의 가중치 값을 특정 값으로 초기화하여 vanishing gradient 문제를 해결한 방법이다. Activation 함수의 종류에 따라 초기의 가중치 값을 다르게 사용할 수 있는데, LeCun, Xavier, He initialization 방법이 대표적인 예시다. 각 initialization 방법에 대한 자세한 설명은 관련 자료를 참고하기 바란다.
PyTorch에서는 기본적으로 모델 생성 시 He initialization 방법으로 가중치를 초기화하는데, 다음과 같이 torch.nn.init을 이용하여 각 layer별로 가중치를 다르게 초기화할 수 있다.

import torch
from torch import nn

class MyModel(nn.Module):
	def __init__(self):
    	super().__init__()
        
        self.linear1 = nn.Linear(5, 10)
        self.relu1 = nn.ReLU()
        self.linear2 = nn.Linear(10, 20)
        self.relu2 = nn.ReLU()
        self.linear3 = nn.Linear(20, 3)
        
		nn.init.xavier_normal_(self.linear1.weight.data)
        nn.init.constant(self.linear2.weight.data)