개요
Gradient descent는 loss function의 값을 최소화하는 매개변수 값을 찾아나갈 때 사용했다. 즉, 모델 학습 시 최적의 매개변수 값을 찾는 과정이므로 gradient descent는 최적화 (optimization) 작업의 일종이라고 볼 수 있다.
그러나 gradient descent는 몇가지 문제점이 발생하는데, 이를 해결하기 위한 여러 가지 알고리즘이 만들어졌다. 지금부터 gradient descent에는 어떤 문제점이 있고, 어떤 방식으로 이를 해결할 수 있는지 알아보자.
1. Problems of Gradient Descent
1) Local minima
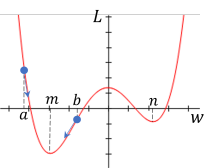
이전 포스트에서 gradient descent를 설명하기 위해 loss function의 예시로 이차함수를 제시했다. 그러나 실제로 모델 학습 시 loss function은 이차함수가 아닌 다른 함수가 될 수 있다. 예를 들어, loss function이 다음 그래프와 같을 때 gradient descent를 적용하면 어떤 결과가 나타나는지 살펴보자.
먼저 매개변수 의 값이 나 일 때 gradient descent를 수행하면 loss 이 최소가 되는 값인 에 가까워질 것이다.
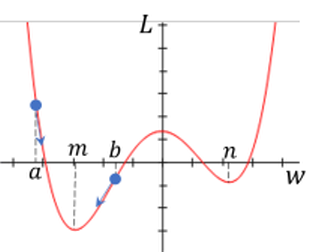
반면에 아래 그림처럼 값이 나 라면 gradient descent를 수행했을 때 에 가까워지게 된다.
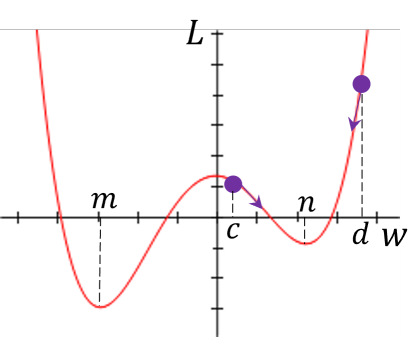
그러나 에서는 이 최소가 되지 않는다. 물론 값의 범위가 에서 사이로 한정되어 있으면 이 범위에 한해서는 에서 최소가 될 수 있다. 하지만 gradient descent를 수행하여 에 가까워지면 모델은 학습을 멈추고 매개변수 의 값을 더이상 변경하지 않는다.
이처럼 전체 범위가 아닌 특정 범위 내에서 최소가 되는 지점을 극소 (local minimum) 지점이라 한다. 극소점에서는 미분값이 0이기 때문에 gradient descent를 수행했을 때 매개변수의 값이 극소점에 수렴하고 결국 모델 학습이 중단된다. 그러나 위 그래프와 같이 극소점이 2개 이상일 수 있으며, 이 때 loss function이 최소가 되는 지점은 여러 극소점 중 하나만 해당하기 때문에 loss function이 최소가 아닌 극소점에 수렴하게 되면 이 지점에서 학습이 중단되어 모델이 제대로 학습하지 못하게 된다.
2) Plateau
이번에는 loss function이 다음 그래프와 같을 때, 와 에서 gradient descent를 수행해보자.
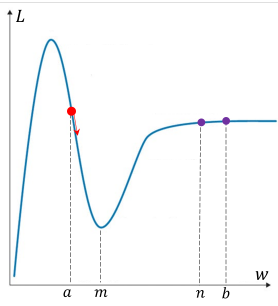
매개변수 의 값이 일 때 gradient descent를 수행하면 이 최소가 되는 에 수렴할 것이다. 그러나 에서는 gradient descent를 수행하지 않는데, 이미 에서의 미분값이 0이기 때문에 gradient descent를 할 필요가 없으며, 이는 값이 이상인 모든 값에 대해 동일한 현상이 나타난다.
이와 같이 미분값이 0인 지점이 하나의 값이 아닌 구간으로 나타날 때, 그 구간은 plateau (고원)에 해당하며 plateau는 극소값이 무한개로 존재한다고 생각할 수 있다. plateau 구간에서는 gradient descent를 수행해도 매개변수의 값이 변하지 않기 때문에 만약 매개변수의 초기값이 이 구간에 해당한다면 모델은 더이상 학습하지 않게 된다.
3) Small or Large learning rate
Learning rate는 gradient descent를 수행할 때 다음 매개변수의 값을 얼마나 증감시킬지를 결정한다. 아래 그림처럼 learning rate의 값이 적절하면 loss가 최소가 되는 최적 지점에 금방 도달할 수 있지만, learning rate가 너무 작으면 최적 지점에 도달하기 위해 학습을 많이 반복해야 하고, 반대로 learning rate가 너무 크면 오히려 최적 지점에 도달할 수 없는 문제가 발생한다.
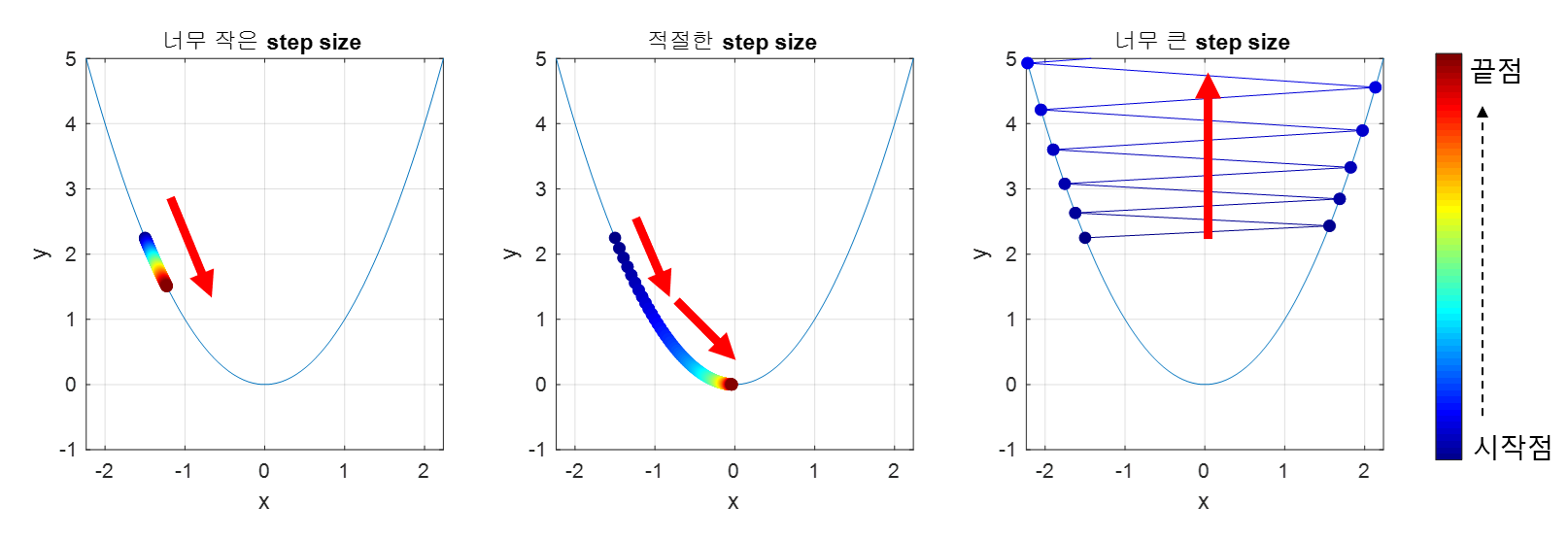 출처: https://raw.githubusercontent.com/angeloyeo/angeloyeo.github.io/master/pics/2020-08-16-gradient_descent/pic4.png
출처: https://raw.githubusercontent.com/angeloyeo/angeloyeo.github.io/master/pics/2020-08-16-gradient_descent/pic4.png
4) Large Batch size
Gradient descent에서는 모든 데이터를 사용하여 gradient를 계산하고 매개변수의 값을 업데이트한다. 그러나 모델의 학습에 사용되는 데이터는 그 샘플의 개수가 매우 많기 때문에 gradient를 계산하는데 메모리 소비량이 많아지고 시간이 오래 걸려 학습 시간이 지나치게 길어지는 단점이 있다.
2. Solutions for Gradient Descent
1) Stochastic Gradient Descent
Stochastic Gradient Descent (SGD)는 모든 데이터가 아닌 하나의 데이터 샘플을 무작위로 뽑아 해당 샘플에 대해서만 gradient descent를 수행한다. SGD는 연산량이 적고 메모리 소비량이 크게 줄어들어 loss function이 최소가 되는 지점에 빠르게 수렴할 수 있다. 그러나 아래 그림처럼 최소점에 수렴하지 못할 수 있고 수렴하는 동안 진폭이 크다는 단점이 있다.
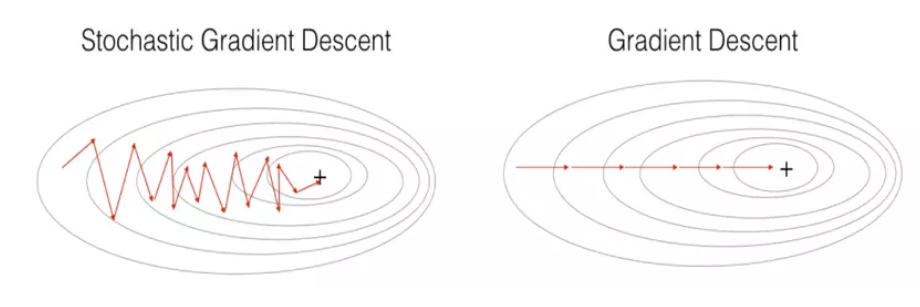 출처: https://i.stack.imgur.com/G7BBG.png
출처: https://i.stack.imgur.com/G7BBG.png
2) Mini Batch Size
Batch의 크기를 모든 데이터보다 작은 개수로 지정하여 여러 개의 batch로 분할한 뒤, 각 batch에 대해 gradient descent를 수행한다. 아래 그림처럼 mini batch size를 사용하면 일반적인 gradient descent보다 연산량이 적고, SGD보다 안정적으로 수렴할 수 있다.
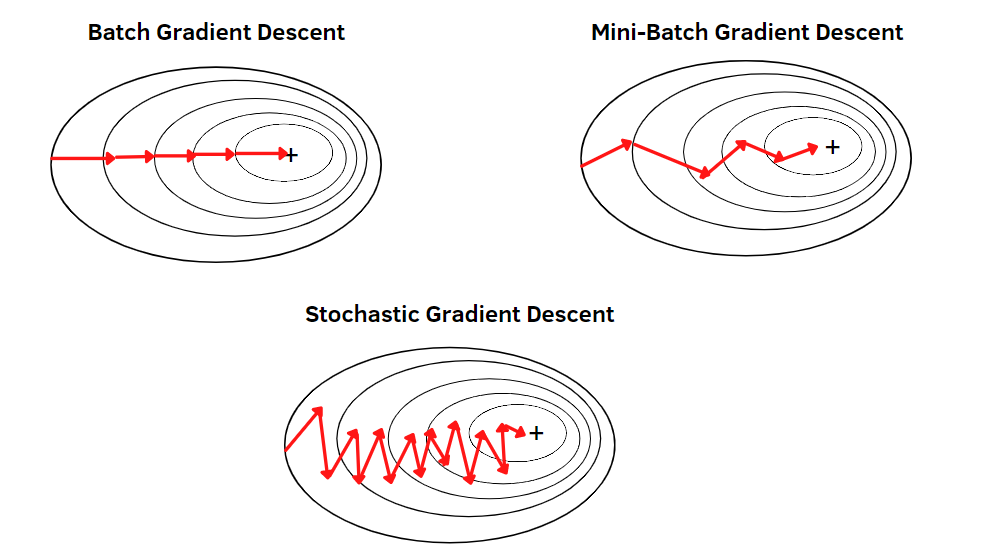 출처: https://editor.analyticsvidhya.com/uploads/58182variations_comparison.png
출처: https://editor.analyticsvidhya.com/uploads/58182variations_comparison.png
3) Momentum
Gradient descent 수행 시 관성 (momentum)을 더하면 과거의 이동 방향을 더하여 기존의 step size보다 더 크게 이동할 수 있다. 즉, 아래의 그림처럼 momentum이 없을 때는 local minimum 지점인 에 수렴하여 매개변수가 더 이상 업데이트되지 않지만 momentum을 더하게 되면 local minimum 지점을 지나서 global minimum 지점인 으로 수렴이 가능하게 된다.
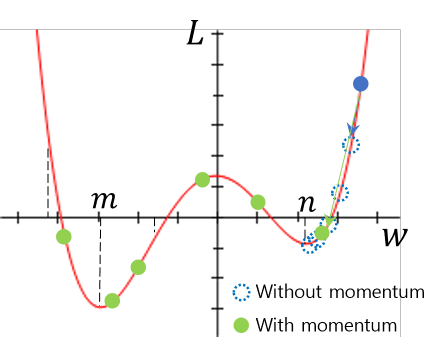
이 과정을 수식으로 나타내면 다음과 같다.
여기서 는 물리적인 속도, 는 momentum이 적용된 속도이다. 즉, 매개변수 업데이트 과정은 기존의 gradient descent에 momentum이 추가되었다고 생각할 수 있다.
4) Adaptive learning rate
Adaptive learning rate는 매개변수를 업데이트할 때 learning rate를 변화시켜 step size를 다르게 설정하는 방법이다. 이 방법의 기본 아이디어는 지금까지 많이 변화했던 매개변수는 step size를 줄여 변화량을 줄이고, 반면에 지금까지 적게 변화했던 매개변수는 step size를 키워 변화량을 늘리는 것이다.
변화량이 큰 매개변수는 loss가 최소가 되는 최적점에 거의 도달했을 가능성이 크기 때문에 이후에 step size를 줄이면 최적점을 지나치지 않고 수렴할 수 있다. 반면 변화량이 적은 매개변수는 최적점에 도달하려면 많은 step이 남아있기 때문에 step size를 키워 loss를 빠르게 줄이는 것이 adaptive learning rate의 핵심이다.
Adaptive learning rate에서는 매개변수 업데이트 시 step size를 얼마나 키우거나 줄일지에 따라 Adagrad, AdaDelta, RMSProp 알고리즘으로 세분화할 수 있다.
5) Other methods
아래 그림과 같이 지금까지 제시한 방법을 혼합한 Adam, NAdam 등의 최적화 알고리즘 등이 있다.
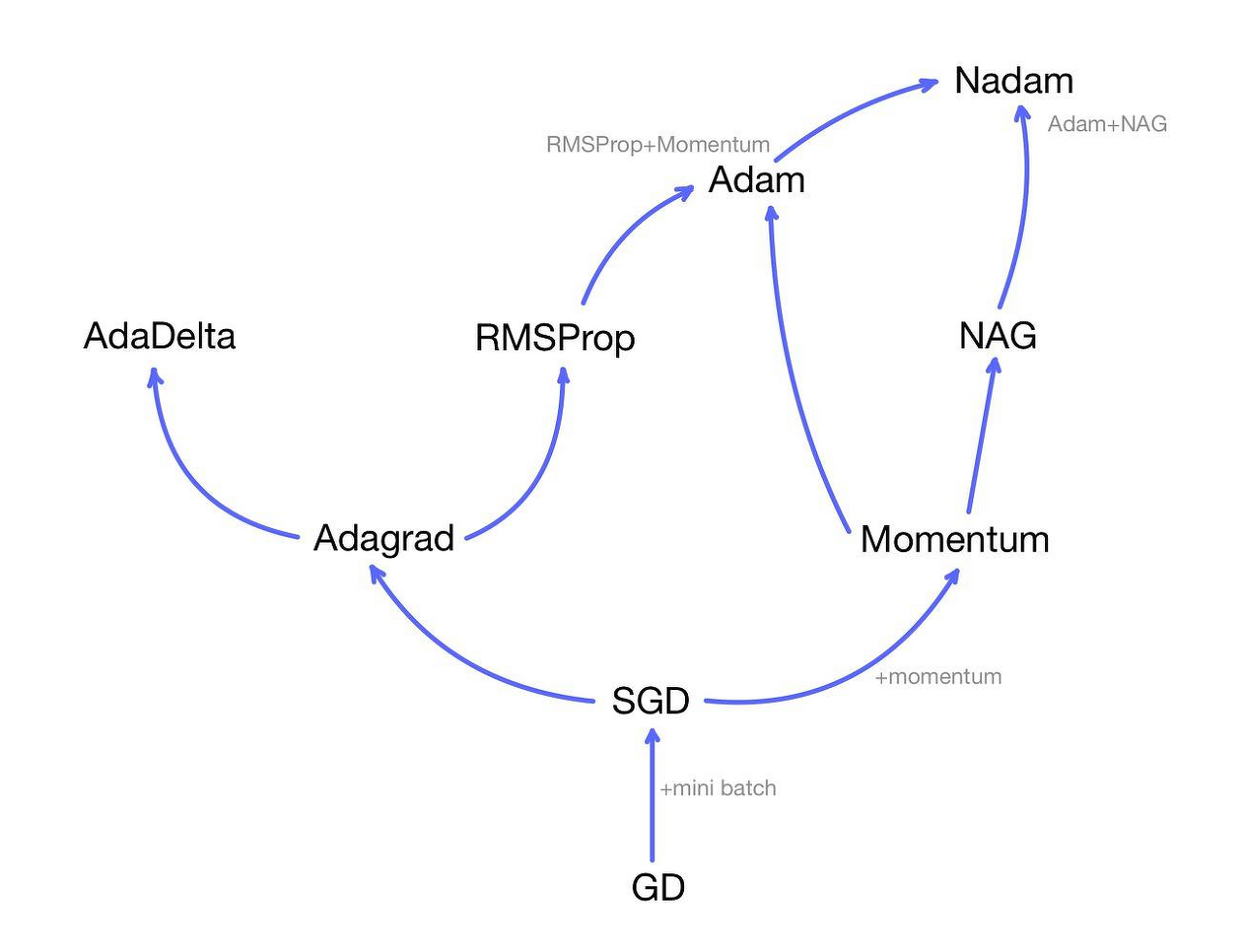 출처: https://arxiv.org/abs/1609.04747
출처: https://arxiv.org/abs/1609.04747
이외에도 PyTorch에서는 torch.optim에서 다양한 매개변수의 최적화 알고리즘을 제공하고 있다.
