개요

기계학습에서의 회귀분석(regression)은 주어진 입력값과 그에 상응하는 출력값에서 학습을 통해 둘 사이의 최적의 상관관계를 찾는 것을 목표로 하고 있다. 예를 들어, 데이터가 아래 그림처럼 분포하면 이들을 종합하여 1차 함수로 근사시켜 표현할 수 있다. 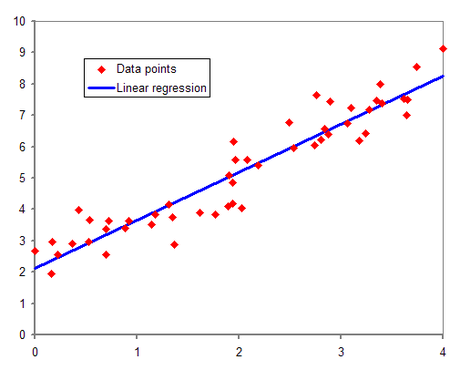이 때, 주어진 데이터에 근사하는 1차함수를 모델, 이 모델의 출력값과 실제 데이터의 출력값이 최대한 비슷해지도록 모델을 조정하는 과정을 학습이라고 생각할 수 있다.

1. Regression for Univariate Dataset

개요에서 제시한 데이터는 입력값 하나에 출력값이 하나인 특징을 가진다. 즉, 하나의 입력값으로 출력값이 결정되기 때문에 이러한 데이터를 univariate data라 한다.
이 데이터에 대한 모델은 1차함수이므로 $y=wx+b$로 표현 가능하며, $w$의 값을 가중치 (weight), $b$의 값을 bias라 한다. 즉, 모델을 학습하는 과정은 이 $w$와 $b$의 값을 조정하며, 입력값 $x$에 대해 모델이 계산한 $y$값과 실제 데이터의 출력값 간의 오차를 최소화하는 것이 모델 학습의 최종 목표가 된다. 이 때, 학습을 하면 $w$와 $b$의 값이 변하므로 이들을 모델의 매개변수 (parameter)라 부른다.

이제 PyTorch를 이용하여 이 과정을 구현해보자.

1) Dataset generation

먼저 개요에 제시한 데이터와 유사한 분포를 갖는 데이터를 만들어보자.

import numpy as np

x = np.arange(0, 5, 0.05)
y = 2 * x + 3 + np.random.randn(100)

numpy의 arange로 0에서 5까지 0.05 간격으로 총 100개의 입력 데이터를 생성하고 $x$에 2를 곱하고 3을 더한 뒤 randn으로 임의의 값을 더해 출력값 $y$를 생성했다. matplotlib.pyplot으로 그 결과를 확인해보자.

import matplotlib.pyplot as plt

plt.xlim([0, 5])
plt.plot(x, y, 'o', markersize=2)
plt.show()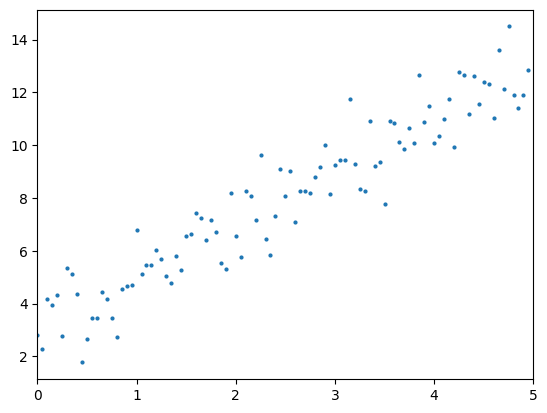

2) Model creation

이제 위 그래프에 표시된 데이터를 계산할 수 있는 모델을 만들어보자. 그러면 오차를 어떻게 정의할지, 매개변수는 어떤 방식으로 조정할지 결정해야 한다.

(1) Loss function

먼저 오차를 어떻게 계산할지 생각해보자. 간단하게 생각할 수 있는 방법은 실제 데이터의 출력값에서 모델이 계산한 값을 빼는 것이다.
그런데 이 방식은 한가지 문제점이 있다. 각각의 입력값에 대한 오차를 계산하면 100개의 서로 다른 오차값이 나올텐데, 그냥 뺄셈을 하다보니 그 값이 양수 또는 음수가 될 수 있는 것이다. 이 값들을 단순히 종합하여 평균값을 산출한다면 모든 오차값을 제대로 대표하지 못하게 된다. 따라서 오차값에 부호를 제거한 후 평균값을 산출해야 하는데, 이는 각 오차값에 절대값이나 제곱을 취하여 해결할 수 있다. 이 과정을 수식으로 표현해보자.

$L=\cfrac{1}{n}\sum_{i=1}^n \left|y_i-\hat{y_i} \right|$

$L=\cfrac{1}{n}\sum_{i=1}^n \left(y_i-\hat{y_i} \right)^2$

위 수식처럼 오차를 구하는 함수 ($L$)를 loss function, loss function으로 부터 얻은 값 ($L$의 값)을 loss라고 한다. 수식에 표기된 $y_i$는 실제 데이터의 출력값, $\hat{y_i}$는 모델의 계산값이고 $n$은 평균값을 산출할 각 오차값의 개수를 뜻한다. 예시에서 오차값이 총 100개이므로 $n$값은 100에 해당한다.
첫번째 수식처럼 각 오차값에 절대값을 취해 평균을 산출한 loss를 L1 loss 또는 Mean Absolute Error (MAE), 두번째 수식처럼 각 오차값에 제곱을 취해 평균을 산출한 loss를 L2 loss 또는 Mean Squared Error (MSE)라 부른다.

이외에도 다양한 종류의 loss function들이 존재하며, PyTorch에서는 위 수식처럼 loss를 계산하는 함수를 torch.nn 패키지 내의 클래스나 torch.nn.functional 패키지 내의 함수로 구현할 수 있다. 기계학습 또는 딥러닝에서 모델의 task (regression, classification, object detection, recommendation 등)에 따라 주로 사용하는 loss function이 상이하므로 관련 문서를 참고하여 언제 어떤 loss function을 사용하는 것이 적절한지 사전에 파악하는 것이 좋다. 예를 들어, 위에서 언급한 L1 loss와 L2 loss는 다음과 같이 구현할 수 있다.

import torch.nn

loss_fn = nn.L1Loss() # L1 Loss (MAE)
loss_fn = nn.MSELoss() # L2 Loss (MSE)
...
# In the training loop
loss = loss_fn(pred, y)

import torch.nn.functional as F

...
# In the training loop 
loss = F.l1_loss(pred, y) # L1 loss
loss = F.mse_loss(pred, y) # L2 loss

(2) Parameter optimizer

(1)절에서 loss function으로 오차를 정의했다면, 이제 매개변수를 어떻게 조정할지 생각해보자. 위 예시에서 모델의 매개변수는 $w$와 $b$ 두개가 있다.
예를 들어, $w$에 대한 loss function의 그래프가 다음과 같고, 현재 $w$의 값이 $a$일 때 다음 학습때 $w$의 값은 $a$보다 커야 할까 작아야 할까?
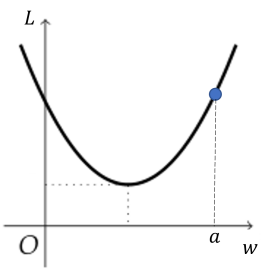정답은 작아져야 한다. 모델 학습의 목표가 loss, 즉 오차를 최소화하는 것임을 생각해보면 loss가 최소가 되는 지점으로 $w$값을 조정해야 한다. 따라서 $a$보다 왼쪽 지점으로 이동해야 한다.
이는 해당 지점에서의 기울기, 즉 미분값으로도 생각할 수 있는데, 아래 그림처럼 $w$값이 $a$에서 $b$로 감소했다면 미분값도 감소하는 것을 확인할 수 있다.

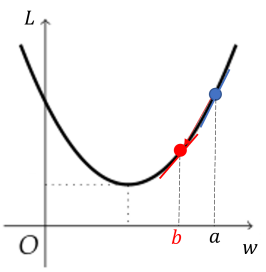
아래 그림처럼 반대의 경우도 생각해보자. 이때는 $w$의 값이 $a$에서 $b$로 증가해야 하며 이에 따라 미분값도 증가하는 것을 확인할 수 있다.

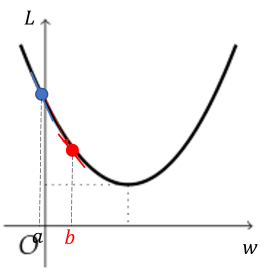
이와 같은 과정으로 모델의 매개변수를 조정하는 방법을 경사 하강법 (gradient descent)이라 부른다.
그런데 위 과정에서는 다음 학습 시 매개변수 값의 증감 여부는 알 수 있어도 얼마나 증감시켜야 하는지는 알 수 없다. 따라서 임의의 값을 부여하여 일정한 간격만큼 증감시키도록 하는데, 이 값을 학습률 (learning rate)이라 부른다.

위 과정을 종합하여 매개변수 $w$와 $b$를 조정하는 과정을 수식으로 나타내면 다음과 같이 쓸 수 있다.

$\hat{w} = w - \alpha \cfrac{\partial{L}}{\partial{w}}$, $\hat{b} = b - \alpha \cfrac{\partial{L}}{\partial{b}}$

$w$와 $b$는 초기의 매개변수 값, $\hat{w}$와 $\hat{b}$는 다음 학습 후 매개변수 값, $\alpha$는 학습률, $\cfrac{\partial{L}}{\partial{w}}$, $\cfrac{\partial{L}}{\partial{b}}$는 초기 매개변수 값에 대한 loss function의 미분값에 해당한다.

PyTorch에서는 gradient descent에 기반하여 최적의 매개변수 값을 찾을 수 있는 다양한 종류의 optimizer를 torch.optim 패키지에서 제공하고 있다. 이렇게 여러가지의 optimizer가 만들어진 이유에 대해서는 추후 포스트에서 설명한다.

3) Model training

1)절에서 제시한 데이터에 대해 regression을 진행해보자. 우리는 1차함수를 찾는 것이 목표이므로 이와 같은 regression을 linear regression이라 한다.
위 데이터의 그래프를 보면 직관적으로 regression이 가능하다. 그러나 프로그램으로 이 과정을 구현하기 어려워 모델을 학습시키는 과정이 필요하다. 그래서 loss function과 parameter optimizer를 사용한다.
여기서는 loss function으로 L2 loss를, optimizer로 gradient descent를 사용하겠다. 먼저 수식으로 loss function이 최소가 되도록 하는 매개변수 값을 찾아보자.

Gradient descent와 L2 loss는 다음과 같이 정의했다.

$\hat{w} = w - \alpha \cfrac{\partial{L}}{\partial{w}}$, $\hat{b} = b - \alpha \cfrac{\partial{L}}{\partial{b}}$, $L=\cfrac{1}{n}\sum_{i=1}^n \left(y_i-\hat{y_i} \right)^2$

Linear regression 모델은 $\hat{y_i} = wx_i + b$로 나타낼 수 있으므로 이를 L2 loss에 대입하여 매개변수 $w$와 $b$에 대해 미분해보자.

$L=\cfrac{1}{n}\sum_{i=1}^n \left(wx_i+b-y_i \right)^2$
$\cfrac{\partial{L}}{\partial{w}}=\cfrac{1}{n}\sum_{i=1}^n 2x_i \left(wx_i+b-y_i \right)=\cfrac{1}{n}\sum_{i=1}^n 2x_i \left(\hat{y_i}-y_i \right)$
$\cfrac{\partial{L}}{\partial{b}}=\cfrac{1}{n}\sum_{i=1}^n 2 \left(wx_i+b-y_i \right)=\cfrac{1}{n}\sum_{i=1}^n 2 \left(\hat{y_i}-y_i \right)$

그럼 이 결과를 바탕으로 모델의 학습 알고리즘을 구현해보자.

w, b, lr, epochs = 1.0, 0, 0.01, 100

for epoch in range(epochs):
    loss, w_grad, b_grad = 0, 0, 0
    for x_sample, y_sample in zip(x, y):
        loss += (w * x_sample + b - y_sample) ** 2 / len(y)

        w_grad += 2 * x_sample * (w * x_sample + b - y_sample)
        b_grad += 2 * (w * x_sample + b - y_sample)
        
    w -= lr * w_grad / len(y)
    b -= lr * b_grad / len(y)
    print(f'Loss: {loss:.3f}, weight: {w:.6f}, bias: {b:.6f} 
    		| Epoch: {epoch + 1}')

>> Loss: 33.082, weight: 1.313141, bias: 0.109610 | Epoch: 1
Loss: 23.062, weight: 1.569446, bias: 0.201526 | Epoch: 2
Loss: 16.312, weight: 1.779122, bias: 0.278918 | Epoch: 3
Loss: 11.764, weight: 1.950544, bias: 0.344383 | Epoch: 4
Loss: 8.698, weight: 2.090582, bias: 0.400053 | Epoch: 5
Loss: 6.630, weight: 2.204874, bias: 0.447677 | Epoch: 6
Loss: 5.233, weight: 2.298044, bias: 0.488692 | Epoch: 7
Loss: 4.288, weight: 2.373888, bias: 0.524275 | Epoch: 8
Loss: 3.648, weight: 2.435519, bias: 0.555391 | Epoch: 9
Loss: 3.213, weight: 2.485491, bias: 0.582835 | Epoch: 10
...
Loss: 1.561, weight: 2.485874, bias: 1.443041 | Epoch: 98
Loss: 1.556, weight: 2.483641, bias: 1.450239 | Epoch: 99
Loss: 1.550, weight: 2.481418, bias: 1.457403 | Epoch: 100

학습 과정을 살펴보자. epoch를 반복할수록 loss가 줄어들고 이에 맞춰 매개변수 $w$, $b$의 값이 변한다. 여기서 epoch란 학습할 모든 데이터에 대해 학습을 완료한 횟수를 말한다. 예를 들어, 학습 데이터에 대해 1회 학습을 완료하면 1 epoch라 할 수 있다. 여기서는 epoch 수를 100으로 정했으므로 학습 데이터에 대해 100회 학습을 완료할 때까지 학습을 반복한다.

이제 학습을 완료한 모델을 그래프로 표시해보자.

y_pred = w * x + b
plt.xlim([0, 5])
plt.plot(x, y, 'o', markersize=2)
plt.plot(x, y_pred)
plt.show()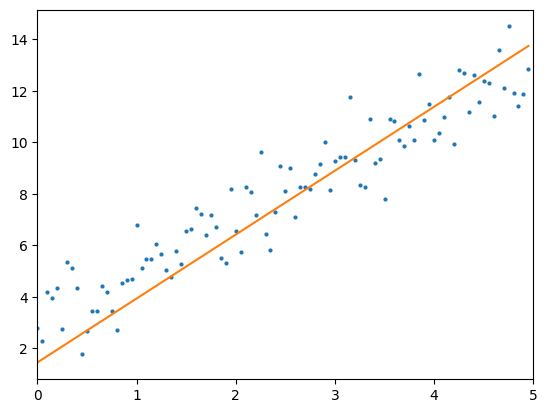

데이터 생성부터 모델 학습까지의 전체 과정을 소스코드로 정리했다.

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(0, 5, 0.05)
y = 2 * x + 3 + np.random.randn(100)
plt.xlim([0, 5])
plt.plot(x, y, 'o', markersize=2)
plt.show()

w, b, lr, epochs = 1, 0, 0.01, 100
for epoch in range(epochs):
    loss, w_grad, b_grad = 0, 0, 0
    for x_sample, y_sample in zip(x, y):
        loss += (w * x_sample + b - y_sample) ** 2 / len(y)

        w_grad += 2 * x_sample * (w * x_sample + b - y_sample)
        b_grad += 2 * (w * x_sample + b - y_sample)
        
    w -= lr * w_grad / len(y)
    b -= lr * b_grad / len(y)
    print(f'Loss: {loss:.3f}, weight: {w:.6f}, bias: {b:.6f} 
    		| Epoch: {epoch + 1}')

y_pred = w * x + b
plt.xlim([0, 5])
plt.plot(x, y, 'o', markersize=2)
plt.plot(x, y_pred)
plt.show()

4) Linear Regression with PyTorch

이번에는 위 과정을 PyTorch를 이용해 구현해보자.

import torch
from torch import nn
import matplotlib.pyplot as plt

x = torch.arange(0, 5, 0.05).unsqueeze(1)
y = torch.mul(x, 2) + 3 + torch.randn(100, 1)
plt.xlim([0, 5])
plt.plot(x, y, 'o', markersize=2)
plt.show()

model = nn.Linear(in_features=1, out_features=1)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
epochs = 100

model.train()
for epoch in range(epochs):
    y_pred = model(x)

    loss = nn.functional.mse_loss(y, y_pred)

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    weight = model.get_parameter('weight')
    bias = model.get_parameter('bias')

    print(f'Loss: {loss:.3f}, weight: {float(weight):.6f}, 
            bias: {float(bias):.6f} | Epoch: {epoch + 1}')

plt.xlim([0, 5])
plt.plot(x, y, 'o', markersize=2)
plt.plot(x, y_pred.detach())
plt.show()

PyTorch에서는 loss function, gradient descent의 계산 과정을 하나의 함수로 구현할 수 있다.

(1) Tensor

데이터의 배열 (array)을 텐서 (Tensor)라 한다. 배열은 차원 (rank)에 따라 0, 1, 2차원 배열 등으로 분류할 수 있는데, 흔히 0차원 배열은 스칼라(scalar), 1차원 배열은 벡터 (vector), 2차원 배열은 행렬 (matrix)라고 부른다. 그래서 3차원 이상의 배열을 주로 tensor라 부르고 있다.

Shape, Dimension

Tensor의 크기 및 차원을 확인할 때는 각각 shape와 dim 함수를 사용할 수 있다. 아래 예시에서 입력 데이터 $x$의 크기와 차원을 확인해보자.

>> x = torch.arange(0, 5, 0.05)
>> x.shape
torch.tensor([100])
>> x.dim()
1
>> x = torch.arange(0, 5, 0.05).unsqueeze(1)
>> x.shape
torch.tensor([100, 1])
>> x.dim()
2
>> x_temp = x.squeeze(1)
>> x_temp.shape
torch.tensor([100])
>> x_temp.dim()
1

torch.arange 함수를 사용하면 0에서 5까지 0.05씩 증가하면서 데이터를 생성한다. 즉, $(0, 0.05, 0.1, ..., 4.95, 5)$라는 크기가 100인 벡터가 만들어진다.
그런데 unsqueeze(dim) 함수를 사용하면 벡터의 원소는 변함이 없지만 100 $\times$ 1인 행렬로 형태가 변한다. 즉, 1차원 벡터에서 2차원 행렬로 바뀌었다. 따라서 unsqueeze(dim) 함수는 dim만큼 tensor의 차원을 늘려준다. 반대로 tensor의 차원을 줄이는 것도 가능한데, squeeze(dim) 함수를 사용하면 된다. 그러면 x_temp처럼 차원이 줄어든 것을 확인할 수 있다.

Broadcasting

4)절에 제시된 출력 데이터 $y$를 계산하는 식을 살펴보자.

>> y = 2 * x + 3 + torch.randn(100, 1)

$y$는 행렬 $x$에 2를 곱한 뒤 3과 난수로 생성된 100 $\times$ 1 행렬을 더했다. 그런데 이 과정에서 의문이 생긴다. 행렬과 상수를 어떻게 더할 수 있는 것일까?

원칙적으로 수학에서는 행렬과 상수를 직접 더할 수 없다. 그러나 크기가 동일한 두 행렬은 서로 더할 수 있다. PyTorch는 이런 점을 이용하여 행렬과 상수를 더할 때는 상수를 더하고자 하는 행렬과 같은 크기의 행렬로 만들어 덧셈을 수행한다. 이 때 만들어지는 행렬의 원소는 모두 같은 상수 값이다. 이렇게 크기나 차원이 다른 두 tensor를 더하기 위해 크기와 차원을 변경하여 연산이 가능하도록 하는 과정을 broadcasting이라 한다. 즉, 아래의 과정과 동일하다고 볼 수 있다.

y = 2 * x + torch.randn(100, 1)
b = 3 * torch.ones(100, 1)
y = y + b

(2) nn.Module

PyTorch에서는 모델을 nn.Linear 클래스를 사용해 구현하고 있다. nn.Linear 클래스는 nn.Module을 상속받은 클래스로, 이를 상속받는 클래스는 nn.Linear 외에도 여러 클래스가 있다. torch.nn 패키지 내에 클래스들의 목록이 있으니 참고하기 바란다. 만약에 여러가지 모델 클래스를 조합하여 자기만의 고유한 모델을 만들고자 할 때도 nn.Moudle 클래스를 상속받아 구현하는 것이 좋다.
torch.nn에 정의된 다른 클래스들에 대한 설명은 추후에 다른 모델을 만들어 사용할 때 설명하도록 하고, 우선 예시에서 사용된 nn.Linear 클래스에 대해 자세히 살펴보자.

model = nn.Linear(in_features=1, out_features=1)
...
# In the training loop
	y_pred = model(x)

학습 시작 전 객체 model을 생성하고, 학습 시 입력 변수 x를 사용하여 y_pred 값을 계산하고 있다.

nn.Linear로 모델을 생성할 때는 입력 변수로 in_features와 out_features의 정수 값이 필요하고 옵션으로 bias의 bool 값 (True/False)이 있다.
bias는 linear regression 모델 학습 시 매개변수 $b$ 값을 학습할지 여부를 결정한다. 기본값은 True로 설정되어 있는데, 본 예시에서도 $b$ 값을 학습하여 그 값이 변하고 있으므로 기본값 그대로 사용했다.
in_features와 out_features는 입력 데이터와 출력 데이터의 차원 (dimension) 수를 결정한다. 예시에 제시된 입력과 출력 데이터는 모두 1차원 스칼라 값이므로 in_features와 out_features 값 모두 1이다.

그러면 모델을 생성하고 학습하는 과정을 PyTorch를 사용하지 않았을 때와 사용했을 때의 차이점을 비교해보자.

Weight, Bias initialization

PyTorch를 사용하지 않았을 때는 w, b = 1, 0으로 weight와 bias 값을 각각 1과 0으로 초기화했다. 그런데 PyTorch를 사용하면서 이 과정이 보이지 않는다. PyTorch에서는 어떤 방식으로 weight와 bias를 초기화하는 것일까?
nn.Linear에서는 uniform distribution인 $U\left(-\sqrt{k}, \sqrt{k}\right) (k=1/(\text{in\_features}))$에서 임의의 값으로 초기화하고 있다. 이와 같은 초기화 방식을 kaiming initialization이라 하며, weight/bias initialization에 대한 상세 설명은 추후 포스트에서 진행할 예정이다.

(3) Batch, Gradient

Gradient

PyTorch를 사용하지 않았을 때는 모델 학습 시 반복문을 이용하여 전체 데이터셋에서 입력과 출력 데이터를 한 쌍씩 추출한 후, loss와 해당 입출력 데이터 샘플에서 loss function을 매개변수 w와 b에 대해 각각 미분한 값을 계산했다. 이처럼 한 함수를 여러 개의 변수에 대해 개별적으로 미분하여 (편미분) 하나의 벡터로 표현한 것을 gradient라고 한다. 즉, 함수 $f$를 변수 $x_1, x_2, ..., x_n$에 대해 편미분한 결과이며 이를 수식으로 표현하면 다음과 같이 나타낸다.

$\nabla{f} = \left[\cfrac{\partial{f}}{\partial{x_1}}, \cfrac{\partial{f}}{\partial{x_2}}, ..., \cfrac{\partial{f}}{\partial{x_n}}\right]$

Batch

그런데 PyTorch에서는 반복문을 사용하지 않고 loss와 gradient를 계산한다. 즉, 100개의 데이터 샘플에 대해 일괄적으로 연산이 가능하다.
앞서 언급한 shape 함수로 입출력 데이터와 매개변수 w, b의 크기를 확인해보자.

>> x.shape
tensor([100, 1])
>> y.shape
tensor([100, 1])
>> y_pred.shape
tensor([100, 1])
>> weight.shape
tensor([1, 1])
>> bias.shape
tensor([1])

PyTorch에서 모델의 매개변수는 nn.Module의 get_parameter 함수를 이용하면 매개변수의 정보를 얻을 수 있다. 이 때, 입력 변수로 매개변수의 이름을 입력해야 하는데, 이는 다음과 같이 named_parameters 함수를 이용하면 얻을 수 있다.

>> for name, param in model.named_parameters():
...	   print(name, param)
weight Parameter containing: tensor([[0.6616]], requires_grad=True)
bias Parameter containing: tensor([0.8800], requires_grad=True)

Linear regression 모델은 1차함수 $\hat{y}=wx+b$로 나타낼 수 있다. PyTorch를 사용하지 않았을 때는 $x$, $\hat{y}$, $w$, $b$ 모두 스칼라 값에 해당한다. 그러나 PyTorch에서는 $x$, $\hat{y}$, $w$는 2차원 행렬로 바뀌었다. 즉, $x$와 $\hat{y}$는 크기가 100 $\times$ 1인 행렬, $w$는 크기가 1 $\times$ 1인 행렬이다. $b$는 여전히 1차원 스칼라 값이지만, $\hat{y}$를 계산할 때 크기가 100 $\times$ 1인 행렬로 확장하는 broadcasting 과정이 적용된다.

이처럼 PyTorch에서는 학습할 데이터 샘플들을 여러개씩 묶어서 일괄적으로 연산이 가능한데, 이러한 묶음들을 batch라고 한다. 본 예시에서는 batch가 1개이며, 그 batch의 크기는 100이라고 할 수 있다. batch의 크기를 조절하는 것도 가능한데, batch의 크기를 조절하는 이유와 그 효과에 대해서는 추후에 설명한다.

(4) Forward propagation, Back propagation, Optimizer

Optimizer

2).(2)절에서 gradient descent의 원리를 소개했다. 이 원리를 이용하여 기존에는 매개변수 $w$, $b$에 대한 loss function의 미분값을 직접 계산하여 learning rate를 곱한 뒤 이를 기존의 매개변수 값에서 각각 차감했다.
반면 PyTorch에서는 optimizer의 종류와 learning를 미리 정의한 다음, 학습 시 zero_grad 함수로 매개변수에 대한 gradient를 먼저 0으로 초기화한 후, backward 함수로 각 매개변수에 대한 gradient 값을 모두 계산하고, step 함수로 gradient descent 과정을 수행한다. 즉, 다음 과정은 서로 같은 역할을 한다고 생각할 수 있다.

# Gradient initialize
w_grad, b_grad = 0, 0
>> optimizer.zero_grad()

# Compute gradient
w_grad += 2 * x_sample * (w * x_sample + b - y_sample)
b_grad += 2 * (w * x_sample + b - y_sample)
>> loss.backward()

# Gradient descent
w -= lr * w_grad / len(y)
b -= lr * b_grad / len(y)
>> optimizer.step()

Forward Propagation

모델이 어떤 값을 입력받아 특정 값을 출력하는 과정을 forward propagation이라 한다. 본 예시에서 y_pred를 구하는 과정에 해당한다.
기존에는 y_pred를 구하기 위해 매개변수 w와 b의 값을 계산한 후, linear regression 모델의 식에 x를 대입하여 계산했다. 즉, y_pred = w * x + b로 나타냈다.
그러나 PyTorch에서는 모델을 nn.Module을 사용하여 먼저 정의한 후, 그 모델에 입력 변수로 입력 데이터를 추가하면 y_pred를 얻을 수 있다. nn.Module은 클래스 내부에 forward 메소드를 포함하고 있는데, 이 메소드는 각 모델의 특성에 맞게 forward propagation을 수행할 수 있도록 추상화되어 있다. 본 예시에서 모델 정의에 사용한 nn.Linear 클래스 역시 nn.Module을 상속받은 클래스이므로, nn.Linear는 상속받은 forward 메소드를 $\hat{y} = wx+b$라는 forward propagation을 수행하도록 재정의 (override)했다. 또한 forward 메소드는 호출 가능한 (callable) 메소드이므로 객체와 입력변수만 호출하면 구현할 수 있다.

본 예시에서 정의한 객체 model이 실제로 forward 메소드를 상속받았는지, 호출 가능한지 확인해보자.

>> isinstance(model, nn.Module)
True
>> hasattr(model, 'forward')
True
>> callable(model)
True

확인 결과 객체 model은 nn.Module의 인스턴스 임을 알 수 있다. 그러므로 model에는 forward 메소드가 정의되어 있으며, 또한 호출 가능하다.

Back Propagation

모델의 학습을 위해 forward propagation으로 얻은 결과와 실제 결과값에 대한 loss 값을 구한 후, loss function을 모델의 매개변수로 각각 미분하여 gradient descent로 매개변수의 값을 변경했다.