과제 1 드디어 시작이다.
Assignment 1
Q 1
Q 1.1
def distinct_words(corpus):
""" Determine a list of distinct words for the corpus.
Params:
corpus (list of list of strings): corpus of documents
Return:
corpus_words (list of strings): sorted list of distinct words across the corpus
num_corpus_words (integer): number of distinct words across the corpus
"""
corpus_words = []
num_corpus_words = -1
# ------------------
# Write your implementation here.
corpus_words = {word for doc in corpus for word in doc}
corpus_words = sorted(list(corpus_words))
num_corpus_words = len(corpus_words)
# ------------------
return corpus_words, num_corpus_wordsset을 이용해서 중복된 단어를 제외하고 정렬하는 코드이다.
test용으로 corpus를 다음과 같이 만들어보자.
test_corpus = ["{} All that glitters isn't gold {}".format(START_TOKEN, END_TOKEN).split(" "), "{} All's well that ends well {}".format(START_TOKEN, END_TOKEN).split(" ")]corpus_words의 반환값은 다음과 같다.
['<END>', '<START>', 'All', "All's", 'ends', 'glitters', 'gold', "isn't", 'that', 'well']Q 1.2
일단 한국어로 번역하면,
창 중앙에 있는 단어 앞의 단어 n과 뒤의 단어 n을 고려하여 특정 창 크기 n(기본값 4)에 대한 동시 발생 행렬을 구성하는 방법을 작성합니다. 여기서는 벡터, 행렬 및 텐서를 나타내기 위해 numpy(np)를 사용하기 시작합니다.
일단 우리는
def compute_co_occurrence_matrix(corpus, window_size=4):
함수를 만들어야한다.
이 함수의 반환값은 return M, word2ind 이다
Return:
M (a symmetric numpy matrix of shape (number of unique words in the corpus , number of unique words in the corpus)):
Co-occurence matrix of word counts.
The ordering of the words in the rows/columns should be the same as the ordering of the words given by the distinct_words function.
word2ind (dict): dictionary that maps word to index (i.e. row/column number) for matrix M.
반환값에 대한 설명을 보면 M은 대칭행렬이다. 즉 동시발생 숫자의 개수가 있는 행렬이다.
그리고 word2ind는 행렬 M에 대한 단어를 인덱스(즉, 행/열 번호)에 매핑하는 딕셔너리이다.
test용으로 corpus를 다음과 같이 만들어보자.
test_corpus = ["{} All that glitters isn't gold {}".format(START_TOKEN, END_TOKEN).split(" "), "{} All's well that ends well {}".format(START_TOKEN, END_TOKEN).split(" ")]그럼 corpust는 다음과 같다.
[['<START>', 'All', 'that', 'glitters', "isn't", 'gold', '<END>'], ['<START>', "All's", 'well', 'that', 'ends', 'well', '<END>']]word2ind의 반환값은 다음과 같은 것이다.
{'<END>': 0, '<START>': 1, 'All': 2, "All's": 3, 'ends': 4, 'glitters': 5, 'gold': 6, "isn't": 7, 'that': 8, 'well': 9}M을 숫자 개수 크기의 정방 행렬을 0으로 초기화하고 word2ind를 구한다. 이는 그저 enumerate를 사용하면 된다.
M = np.zeros((num_words,num_words))
for i, word in enumerate(words):
word2ind[word] = i그리고 중심 단어에 대해 window 창으로 주변 단어들의 리스트를 만들자.
우선 문장을 article이라 하자.
article을 반복문을 통해 처음부터 centerword로 정한다.
그리고 center word의 index를 word2ind에서 구한다.
그 다음 context는 article의 주변 단어들이다.
만약 A B C E D 라는 단어에서 window_size는 2이고 B가 center word라면
A, C, E가 주변 단어가 된다.
그 다음 context의 단어들의 for문을 돌려서
word2ind에서 주변단어의 인덱스를 구한뒤
M행렬의 행에는 center, 열에는 context의 인덱스를 넣어 하나씩 더해준다.
for article in corpus:
article_len = len(article)
for i, center in enumerate(article):
center_index = word2ind[center]
context = article[i - window_size : i] + article[i + 1 : i + window_size + 1]
for context_word in context:
context_word_index = word2ind[context_word]
M[center_index, context_word_index] += 1Q 1.3
reduce_k_dim 함수를 구현하자.
한국어로 번역하면
행렬에 차원 축소를 수행하여 k차원 임베딩을 생성하는 방법을 구성합니다. SVD를 사용하여 상위 k개의 성분을 취하고 k차원 임베딩의 새로운 행렬을 생성합니다.
참고: 모든 numpy, scippy, scikit-learn(sklearn)은 SVD의 일부 구현을 제공하지만, Scippy와 sklearn만이 Truncated SVD의 구현을 제공하고, sklearn만이 대규모 Truncated SVD를 계산하기 위한 효율적인 무작위 알고리즘을 제공합니다. 따라서 sklearn.decomposition.Truncated SVD를 사용하십시오.
그러니까 SVD를 이용하여서 행렬의 차원을 축소해야 한다.
그래서 SVD 링크 를 통해 TruncatedSVD 사용법을 알아보자.
parameter로는 reduce_to_k_dim(M, k=2) 이다.
Params:
M (numpy matrix of shape (number of unique words in the corpus , number of unique words in the corpus)): co-occurence matrix of word counts
k (int): embedding size of each word after dimension reduction
M은 아까 구한 행렬이고 k는 차원축소 후의 임베딩 크기이다.
Return:
M_reduced (numpy matrix of shape (number of corpus words, k)): matrix of k-dimensioal word embeddings.
In terms of the SVD from math class, this actually returns U * S
우리는 차원축소된 M을 구해야한다.
이는 svd를 먼저 만들고 fit_transform 함수를 사용하자.
# ------------------
# Write your implementation here.
svd = TruncatedSVD(n_components=k, n_iter = n_iters)
M_reduced = svd.fit_transform(M)
# ------------------Q 1.4
plot_embeddings code를 구현하자.
한국어로,
여기서는 2차원 공간에 2차원 벡터의 집합을 플롯하는 함수를 작성할 것입니다. 그래프의 경우 Matplotlib(plt)을 사용합니다.
이 예에서는 이 코드를 적용하는 것이 유용하다고 생각할 수 있습니다. 미래에 플롯을 만드는 좋은 방법은 Matplotlib 갤러리를 보고 원하는 것과 어느 정도 비슷하게 보이는 플롯을 찾아서 그들이 주는 코드를 적용하는 것입니다.
note를 보면
Plot in a scatterplot the embeddings of the words specified in the list "words".
즉 words 리스트에 있는 word들의 임베딩을 표시한다.
NOTE: do not plot all the words listed in M_reduced / word2ind.
Include a label next to each point.
Params:
M_reduced (numpy matrix of shape (number of unique words in the corpus , 2)): matrix of 2-dimensioal word embeddings
word2ind (dict): dictionary that maps word to indices for matrix M
words (list of strings): words whose embeddings we want to visualize
이다.
흠. 일단 우리는 k=2로 차원을 축소했다.
words에 있는 word 각각에 for문을 돌려서 수행한다.
즉 단어 하나에 점 하나씩 찍히는 것이다.
그래프는 주어진 다음 그림을 참고하여 작성한다.
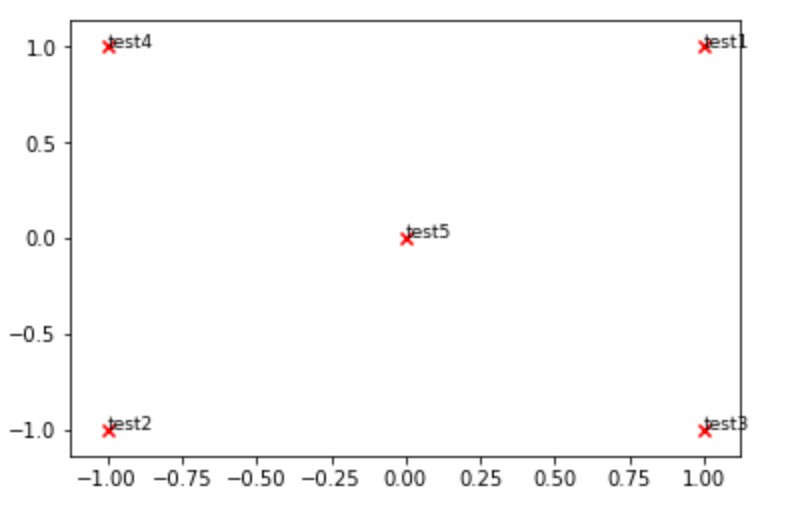
참고로 주석다는 함수는 annotate이다.
# ------------------
# Write your implementation here.
for word in words:
word_index = word2ind[word]
x = M_reduced[word_index, 0]
y = M_reduced[word_index, 1]
plt.scatter(x, y, marker = 'X', color = 'red', s = 80, linewidths = 0)
plt.annotate(word, (x,y))
plt.show()
# ------------------Q 1.5
그래서 이미 작성된 모든 코드를 실행한다면
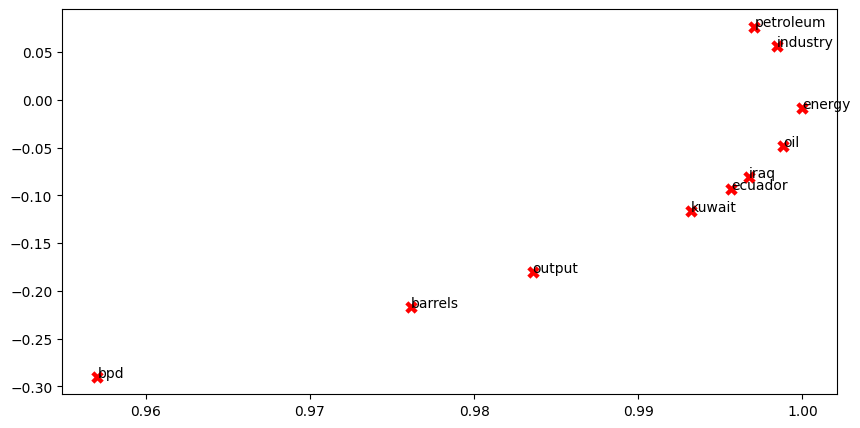
이런 그래프가 생성된다.
그럼 아래 질문에 대해 답을 해보자.
What clusters together in 2-dimensional embedding space? What doesn't cluster together that you might think should have?
위 그림에서 petroleum, industry
energy, oil
iraq, ecuador, kuwait가 묶여있다.
이란과 에콰도르, 쿠웨이트는 오일 수출국이다. 아마 석유 수출국가들은 비슷한 공동 발생 단어들을 공유할 가능성이 높기 때문에 이렇게 묶여 있는 듯 하다.
bpd, barrels, output은 비슷하지만 아마도 단어 발생 횟수가 적은 듯하다.
그리고 crude oil과 petroleum은 동일한 의미이기 때문에 더 가까이 clustered 될 수 있을 듯하다.
Q 2
Prediction-Based Word Vectors (15 points)
에 대해 알아보자.. 드디어 2번 문제이다.
여기서는 GloVe에서 생성된 임베딩에 대해 알아볼 예정이다.
우리는 이제 GloVe와 1번에서 만든 동시 발생 행렬을 비교할 예정이다.
그런데 일단 자료부터 가져와야한다.
맨처음 코드를 실행하면 에러가 발생할 것이다.
이는 vocab이라는 attribute가 수정되어 그렇다.
다음과 같이 수정한다.
def load_embedding_model():
""" Load GloVe Vectors
Return:
wv_from_bin: All 400000 embeddings, each lengh 200
"""
import gensim.downloader as api
wv_from_bin = api.load("glove-wiki-gigaword-200")
print("Loaded vocab size %i" % len(wv_from_bin.key_to_index.keys()))
return wv_from_bin워드 임베딩의 차원을 축소할 것이다.
- Put 10000 Glove vectors into a matrix M
- Run reduce_to_k_dim (your Truncated SVD function) to reduce the vectors from 200-dimensional to 2-dimensional.
이미 주어진 코드를 실행한다.
그럼 error가 또 발생한다.
vocab가 없기 때문이다. 따라서 아래 코드만 수정한다.
words = list(wv_from_bin.key_to_index.keys())Q 2.1
드디어 Q 2.1
아래 그림은 GloVe 임베딩을 그림으로 표시한 것이다.
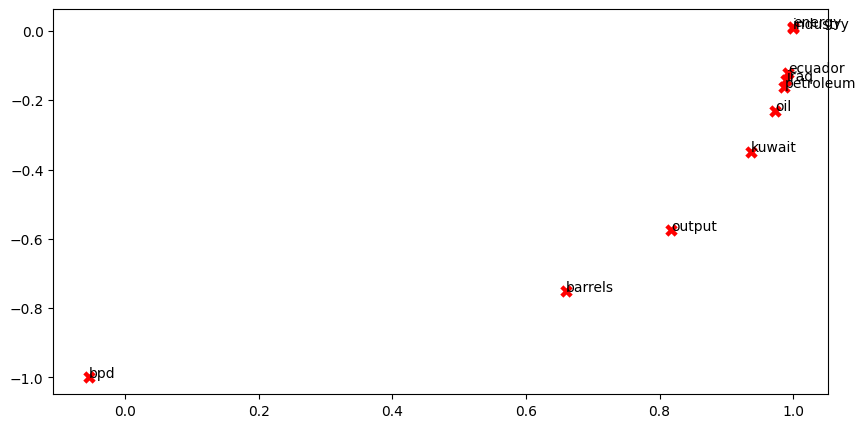
그리고 아래 문제에 대해 답을 해보자.
2차원 매립공간에서 함께 군집하는 것은 무엇입니까?
있어야 한다고 생각하는 것들이 함께 군집하지 않는 것은 무엇입니까? 동반 발생 행렬에서 앞서 생성된 것과 어떻게 다릅니까? 그 차이의 가능한 원인은 무엇입니까?
- 동시 발생 행렬과 다르게, kuwait와 ecuador가 함께 묶여있지 않고 있다.
- industry와 energy가 더 가까이 cluster 되었다.
- oil과 petroleum 이 예상대로 거의 동일한 위치에 있다.
- bpd와 barrels가 더 가까이 붙을 줄 알았는데 더 멀어졌다.
- 동시 발생 행렬은 원유를 주제로한 뉴스로만 훈련을 시켰기 때문이다.
- 반면에 GloVe 벡터는 원유 맥락 밖의 의미 정보까지 포함한다.
- 그래서 국가의 군집 정도가 Glove 벡터에서 좀더 멀어진 것이다.
코사인 유사도 (cosine-similarity)
우리는 이제 단어 벡터를 가지고 있으니까, 단어 벡터들의 유사도 s 를 판단해보자.
Q 2.2
Words with Multiple Meanings
한 단어에는 여러 의미를 가지고 있다.
예를 들어, leaves는 "go_away" 와 "a_structure_of_a_plant" 라는 의미를 가지고 있다.
wv_from_bin.most_similar(word) 를 사용해서 단어들의 의미들을 써보자.
wv_from_bin.most_similar("degrees")그럼 문제에 대해 답을 해보자.
Please state the word you discover and the multiple meanings that occur in the top 10. Why do you think many of the polysemous or homonymic words you tried didn't work (i.e. the top-10 most similar words only contain one of the meanings of the words)?
degrees 에 대한 top 10 비슷한 단어들은 다음과 같았다.
[('celsius', 0.7019519209861755),
('degree', 0.6858925819396973),
('centigrade', 0.6545239686965942),
('fahrenheit', 0.6527740359306335),
('temperatures', 0.6096974611282349),
('temperature', 0.5965989828109741),
('bachelor', 0.58099764585495),
('undergraduate', 0.5485373735427856),
('celcius', 0.547236979007721),
('doctorate', 0.5470802783966064)]degree는 온도의 '도'와 학위라는 의미 두가지를 포함하고 있는데 top 10 단어를 보면 둘다 확인할 수 있다.
다른 의미를 포함하고 있는데 왜 다른 벡터로 표시하지 않냐하면, 많은 경우 대부분의 단어에는 한 의미가 다른 의미를 포함하는 경우가 많기 때문이다.
Q 2.3
우리는 때때로 코사인 유사도 대신 코사인 distance를 통해 유사도를 판단할 수 있다.
하지만 유사한 단어끼리 보다 반대의 단어 끼리의 거리가 더 가까울 수 있다.
예를 들어 w1 = 'happy' 의 경우 w3 = 'sad' w2 = 'cheerful' 에서 w1와 w2의 거리가 w3 거리보다 더 가깝다.
Cosine Distance (w1,w3) < Cosine Distance (w1,w2).
Q. 이러한 예시를 하나 더 찾고, 이러한 이유에 대해 설명해라.
# ------------------
# Write your implementation here.
w1 = "hate"
w2 = "dislike"
w3 = "love"
w1_w2 = wv_from_bin.distance(w1, w2)
w1_w3 = wv_from_bin.distance(w1, w3)
print("비슷한 단어 {} 와 {} 사이의 거리 : {}".format(w1, w2, w1_w2))
print("반대 단어 {} 와 {} 사이의 거리 : {}".format(w1, w3, w1_w3))
# ------------------위 코드를 실행하면,
비슷한 단어 hate 와 dislike 사이의 거리 : 0.5515517294406891
반대 단어 hate 와 love 사이의 거리 : 0.49353712797164917이다. 즉 반대 사이의 거리가 더 가깝다.
단어 사이의 근접성은 문맥을 의미한다. 위 같은 경우에는 hate와 love가 비슷한 맥락에서 사용된다는 의미이다. '나는 초콜릿이 좋아.' '나는 초콜릿이 싫어' 와 같이 비슷한 위치에 hate와 love가 들어가고 따라서 반대 의미의 단어끼리의 근접도는 가까울 수 있다.
Q 2.4
Analogies with Word Vectors
이러한 부등식을 풀어보자
"man : king :: woman : x"
x에는 무엇이 들어갈까? 우리가 생각하기로는 쉽게 queen 이 답이라는 것을 알 수 있다.
다음 코드를 실행하여 한번 찾아보자.
# Run this cell to answer the analogy -- man : king :: woman : x
pprint.pprint(wv_from_bin.most_similar(positive=['woman', 'king'], negative=['man']))결과는 다음과 같다.
[('queen', 0.6978678107261658),
('princess', 0.6081745028495789),
('monarch', 0.5889754891395569),
('throne', 0.5775108933448792),
('prince', 0.5750998258590698),
('elizabeth', 0.5463595986366272),
('daughter', 0.5399126410484314),
('kingdom', 0.5318052768707275),
('mother', 0.5168544054031372),
('crown', 0.5164473056793213)]맨 처음 벡터인 queen을 보아 우리의 예상대로 x를 잘 찾았음을 알 수 있다.
Let m , k , w , and x denote the word vectors for man, king, woman, and the answer, respectively. Using only vectors m , k , w , and the vector arithmetic operators + and − in your answer, what is the expression in which we are maximizing cosine similarity with x ?
그럼 m, k , w를 산술 표현식으로만 나타내서 x를 표현할 수 있을까?
쉽게 나타낼 수 있다.
x k - m + w
(족보에서는 ||k-m|| ||x-w|| 로 나타냈다.)
Q 2.5
: Finding Analogies
그럼 예시를 찾아보자.
pprint.pprint(wv_from_bin.most_similar(positive=['woman','actor'], negative=['man']))
[('actress', 0.857262372970581),
('actresses', 0.6734700798988342),
('actors', 0.6297088265419006),
('starring', 0.6084522008895874),
('starred', 0.5989463925361633),
('screenwriter', 0.595988929271698),
('dancer', 0.5881682634353638),
('comedian', 0.5791140794754028),
('singer', 0.5661861896514893),
('married', 0.5574131011962891)]
결과는 잘 나오는 것을 알 수 있었다.
Q 2.6
2.6: Incorrect Analogy
그럼 부정확한 예시에 대해서도 알아보자.
나는 vegetable : healthy :: fried : x 를 구하고 싶었다.
# ------------------
# Write your implementation here.
pprint.pprint(wv_from_bin.most_similar(positive=['fried', 'healthy'], negative=['vegetable']))
# ------------------답은
[('eating', 0.47669360041618347),
('good', 0.44543972611427307),
('eat', 0.4439126253128052),
("'re", 0.44084489345550537),
('pretty', 0.43743056058883667),
('healthier', 0.4351171851158142),
('sure', 0.42459332942962646),
('think', 0.3994399607181549),
('getting', 0.39766040444374084),
('better', 0.3956679105758667)]로 나왔고
vegetable : healthy :: fried : eating
이 나와버렸다.
Q 2.7
편향은 인공지능을 활용하며 더욱 고정관념을 강화할 수 있기 때문에 문제이다.
다음 셀을 실행해서 결과를 확인해보자.
# Run this cell
# Here `positive` indicates the list of words to be similar to and `negative` indicates the list of words to be
# most dissimilar from.
pprint.pprint(wv_from_bin.most_similar(positive=['woman', 'worker'], negative=['man']))
print()
pprint.pprint(wv_from_bin.most_similar(positive=['man', 'worker'], negative=['woman']))결과는 다음과 같았다.
[('employee', 0.6375863552093506),
('workers', 0.6068920493125916),
('nurse', 0.5837947130203247),
('pregnant', 0.5363885164260864),
('mother', 0.5321308970451355),
('employer', 0.5127025842666626),
('teacher', 0.5099576711654663),
('child', 0.5096741318702698),
('homemaker', 0.5019454956054688),
('nurses', 0.4970572590827942)]
[('workers', 0.611325740814209),
('employee', 0.5983108878135681),
('working', 0.5615329742431641),
('laborer', 0.5442320108413696),
('unemployed', 0.536851704120636),
('job', 0.5278826355934143),
('work', 0.5223963856697083),
('mechanic', 0.5088937282562256),
('worked', 0.5054520964622498),
('factory', 0.4940454363822937)] man -> worker 일때 여자는 employee 였고
woman -> worker 일 때 남자는 workers 였다.
이는 비슷하나 다음 단어들부터는 달랐다.
여자의 경우는 nurse, pregnant, mother 라면 남자의 경우에는 working, laborer, umemployed 였다.
즉 어느정도 편향이 반영되어 결과가 나타났다. 이는 여자가 많이하는 직업과 남자가 많이 하는 직업이 다르기 때문이다.
Q 2.8
Independent Analysis of Bias in Word Vectors
그렇다면 또 다른 편향의 예시는 무엇이 있을까?
# ------------------
# Write your implementation here.
pprint.pprint(wv_from_bin.most_similar(positive=['mongoloid', 'worker'], negative=['caucasian']))
print()
pprint.pprint(wv_from_bin.most_similar(positive=['caucasian', 'worker'], negative=['mongoloid']))
# ------------------
[('employee', 0.4482906460762024),
('driver', 0.414524108171463),
('laborer', 0.40444397926330566),
('technician', 0.3976309895515442),
('surnamed', 0.37281039357185364),
('employer', 0.3728030025959015),
('mechanic', 0.3725651204586029),
('workers', 0.36848387122154236),
('taxi', 0.3541472852230072),
('sanitation', 0.35267239809036255)]
[('workers', 0.6194444894790649),
('employee', 0.5694276094436646),
('working', 0.5499763488769531),
('woman', 0.5463482141494751),
('teacher', 0.5383005738258362),
('work', 0.524975597858429),
('worked', 0.5196768045425415),
('mother', 0.5109690427780151),
('child', 0.49626579880714417),
('job', 0.48688772320747375)] 백인종과 황인종의 경우에도 다른 결과를 느꼈다.
이거 완전 인종차별아님?
2.9
바이어스가 어떻게 단어 벡터에 들어가는지 한 가지 설명을 해주세요. 이러한 바이어스의 근원을 테스트하거나 측정하기 위해 당신이 할 수 있는 실험은 무엇인가요?
당연히 입력 데이터에 편향이 존재하다면 아웃 데이터에도 편향이 존재할 수 밖에...
