Lecture 5

강의 링크

다섯번째 강의 계획은 다음과 같다.
1. Neural dependency parsing
2. A bit more about neural networks
3. Language modeling + RNNs

이전에 그리디 방식까지만 알아봤다면 이번에는 neural dependency parsing에 대해 알아보자.

Neural dependency parsing

사실 이전에 배운 방법은 indicator features를 사용하는데, 여기엔 3가지 문제점이 있다.

• sparse
• incomplete
• expensive computation

parsing의 소요시간 중 95%가 feature를 계산하는데 사용되기 때문에 계산 비용이 높다.

이 과정에서 단어의 의미를 반영하지 못하는 단점이 있다.

이를 해결한 Neural 접근은 dense and compact한 특징 표현을 배우는 것이다.

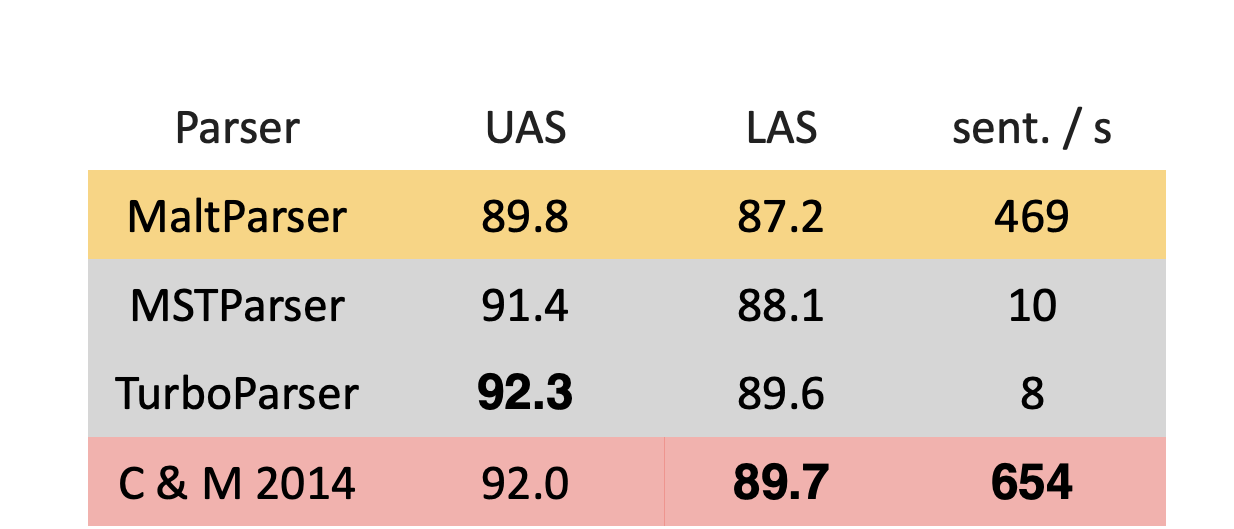
Chen and Manning 이 2014년에 개발한 neual dependency parser는 USA 와 LAS에서도 높은 정확도를 보였고 속도 또한 빨랐다.

(회색은 그래프 기반 파서이다.)

각각의 단어는 d차원의 dense vector로 나타낸다.

• 비슷한 단어는 비슷한 벡터로 기대된다.

또한 part-of-speech tags(POS)와 dependency labels 또한 d 차원의 벡터로 들어간다.

input은 따라서 3가지로 구분한다.

• words
• POS
• arc labels 그리고 stack과 buffer에 있는 것들을 token별로 추출한다.
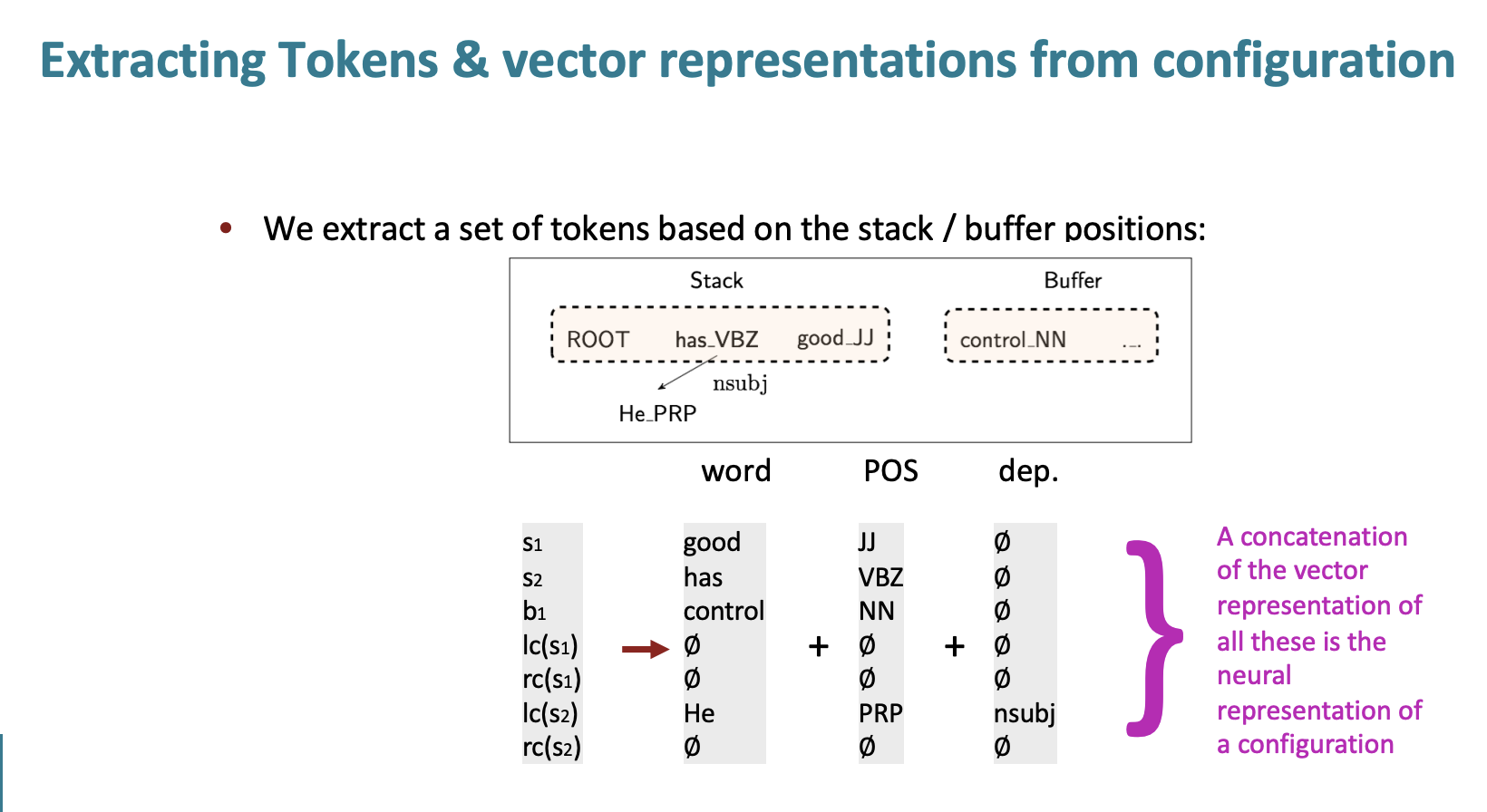
  여기서 has의 POS는 VBZ이다.
  He는 POS가 PRP이고 has와의 nsubj관계이다.

stack과 buffer에 있는 단어 + 단어의 pos + 그리고 dep의 벡터를 원 핫으로 표현한 후에 모두 concat한다. 그 다음 input layer에 넣는다.

히든 레이어에서는 Embedding vector와 Weight matrix를 곱하고 bias vector를 더하는 계산이 진행된다. 여기서는 ReLU 함수를 통해 Hidden vector를 생성한다.

만들어진 Hidden vector를 Softmax layer에서 Softmax함수를 통해 output을 생성한다.

결과적으로 shift, left- arc, right-arc 중 가장 확률값이 높은 경우를 output으로 산출한다.

결과적으로, Chen and Manning의 파싱은 정확도 높고 빠른 parser가 되었다. 전통적인 ML 분류기는 선형 결정 경계를 가졌지만 Neural networks는 더 복잡한 함수를 배울 수 있어서 비선형 경계를 가질 수 있게 되었고 더 정확도가 높을 수 있었다.

그 이후 구글에서 개발된 parser는 더 크고 깊은 networks를 만들거나 beam search를 적용하였다.

Graph-based dependency parser

그래프 기반 파서는 모든 denpendency를 고려한다.

더 자세하고 깊은 내용은 다루지 않지만,
neural dependency parser보다 정확도가 높다.

하지만 굉장히 느리다는 단점을 가지고 있다.

More About Neural Network

Regularization

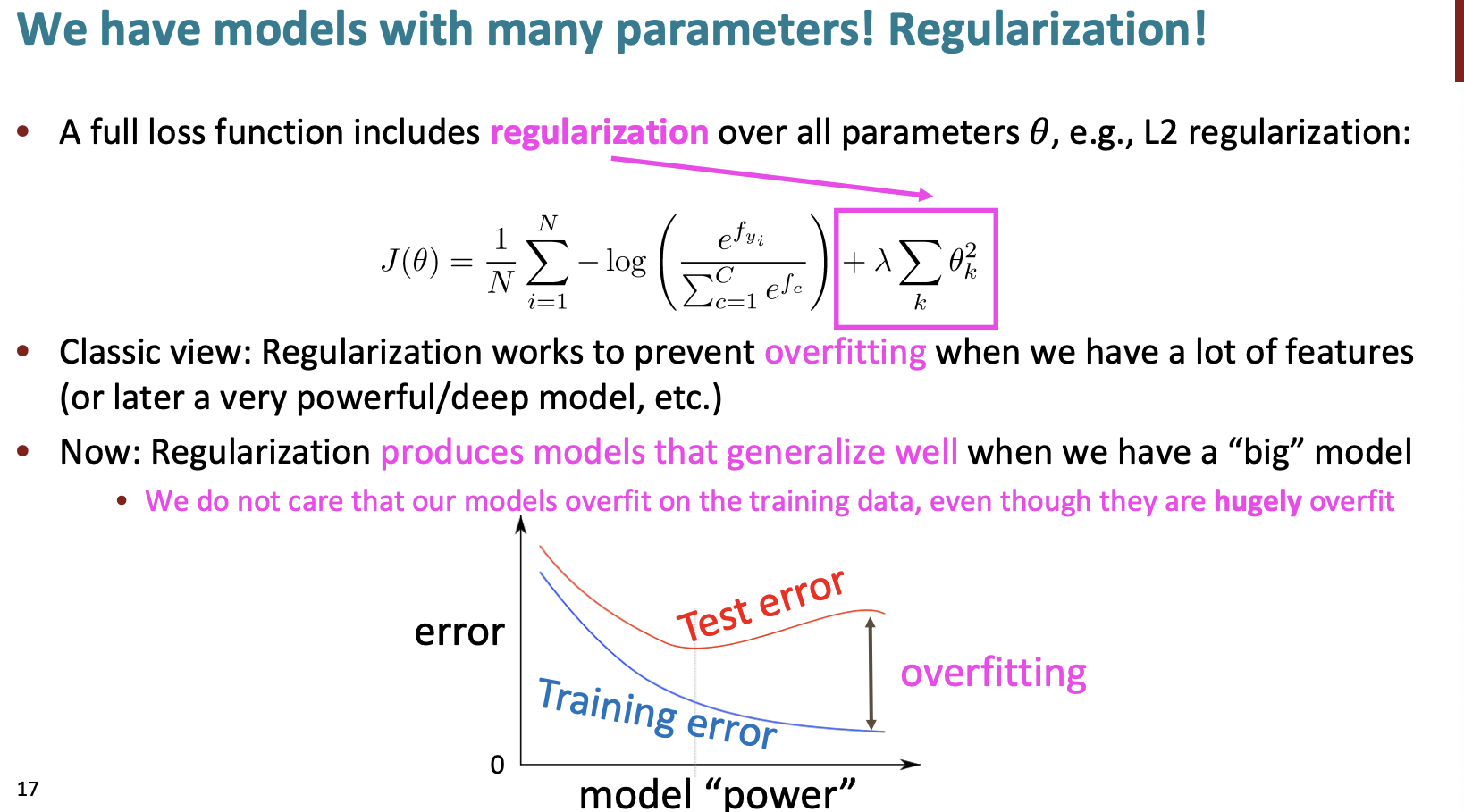
전체 손실 함수에 대해서는 매개변수에 대한 정규화를 포함하고 있다.

정규화는 과적합을 방지한다.

하지만 현재 정규화는 우리가 '큰'모델을 만들 때의 모델의 일반화를 만든다. 우리는 훈련 데이터에 대한 과적합을 생각하지 않는다.

dropout

신경망에 대한 정규화를 수행하는 좋은 방법이다.
신경망에서 과적합을 방지하기 위함이다.

훈련할 때, 일부 뉴런이나 연결을 무작위로 비활성화한다.(0으로 설정)
신경망은 줄어든 뉴런 집합을 사용하여 학습한다. 이는 지나치게 한 뉴런엔 의존을 하는 것을 방지한다.

검증할 때, 모델의 가중치를 반으로 줄인다.(현재는 두배로 늘어났다.)
scaling을 적용하는 것인데 기존에 모델 학습 시 drop-out rate확률로 각 뉴런이 꺼져있었기 때문에 이를 보정하는 것이다.

예외적으로 첫번째 레이어 인풋은 15%만 drop하거나 아니면 아예 drop하지 않는다.

이는 co-adaptation을 방지한다.

이는 Naive Bayes와 logistic regression 모델의 중간정도를 가진다.

Vectorization

행렬이 커지면 for loop을 사용하는 것 보다 행렬 계산을 통해 계산하는 것이 속도가 훨 빠르다.

Non-linearities

1. logistic

가장 일반적인 함수이다. 시그모이드라고도 불린다.

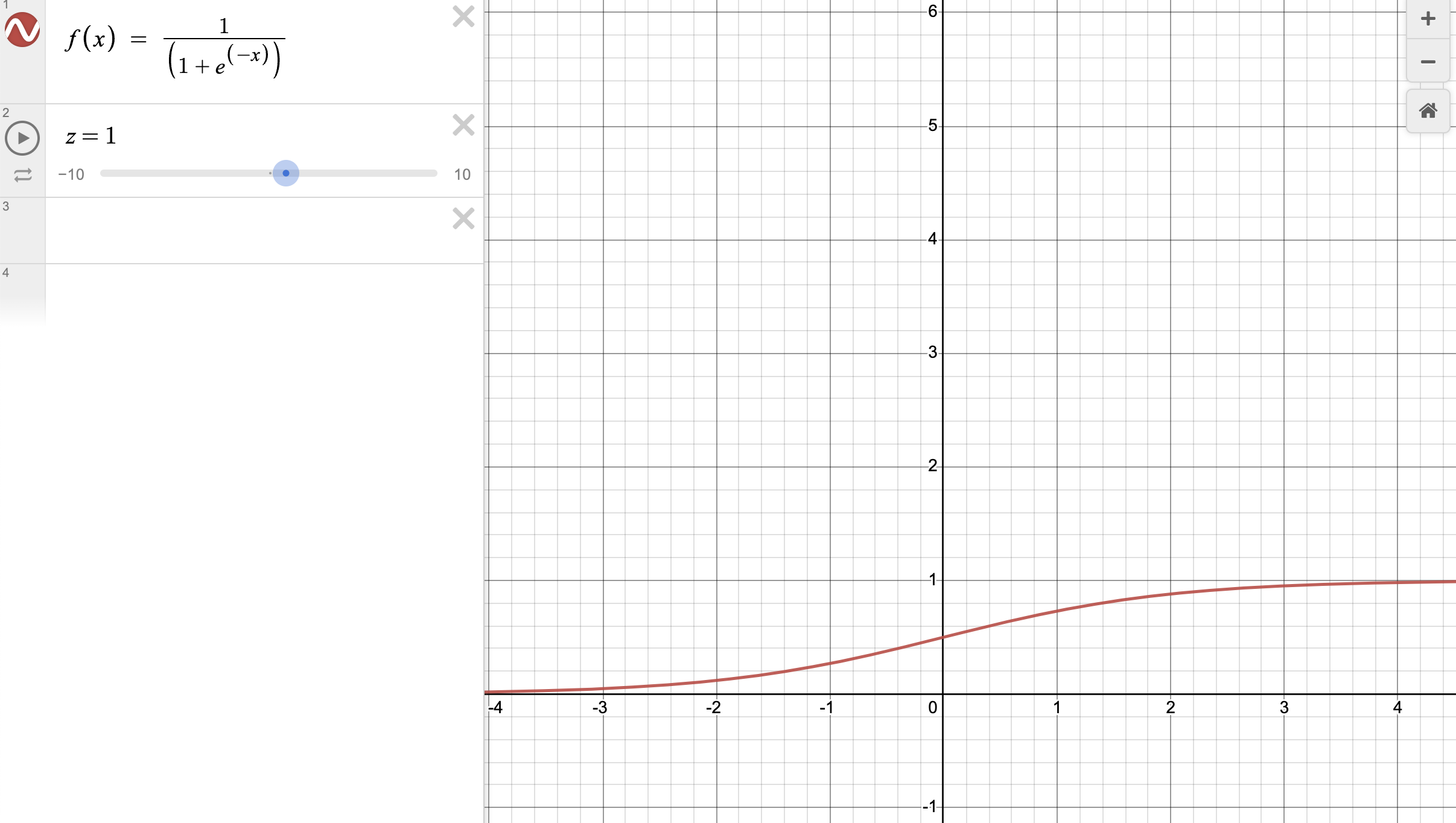
결과값이 항상 0에서 1사이의 값이다.
그래서 항상 양수의 값만 나온다.

2. tanh

양수의 값만 나오는 logistic 함수를 보완함 함수이다.
tanh는 -1에서 1까지의 값이 나온다.

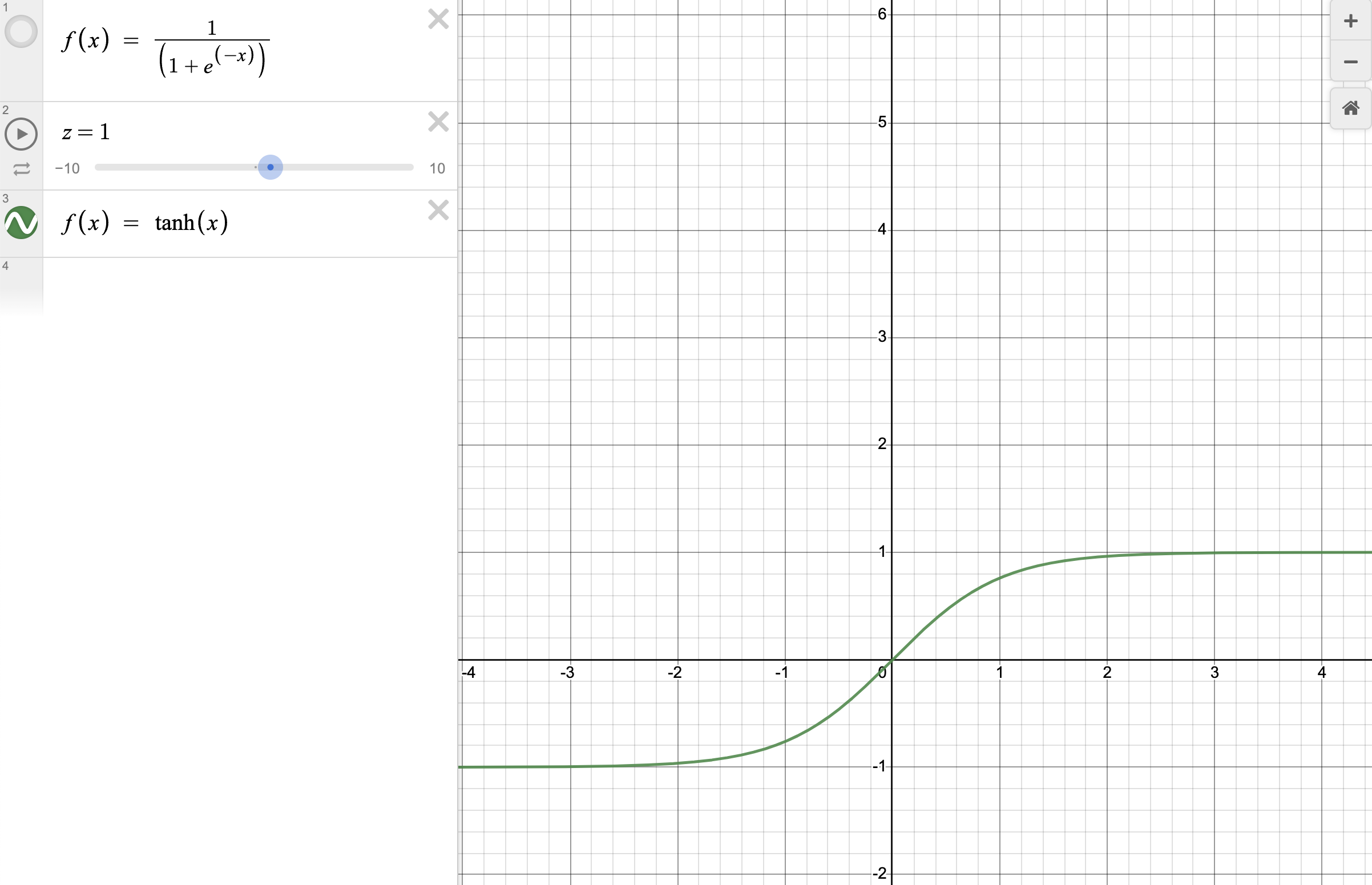
많은 곳에서 logistic과 tanh를 사용하지만 더이상 딥러닝에서 사용되지 않는다.

3. hard tanh

tanh를 선으로 나타낸 것이다.
만약 -1보다 작으면 -1, -1과 1사이면 x, 1보다 크다면 1로 설정한다.

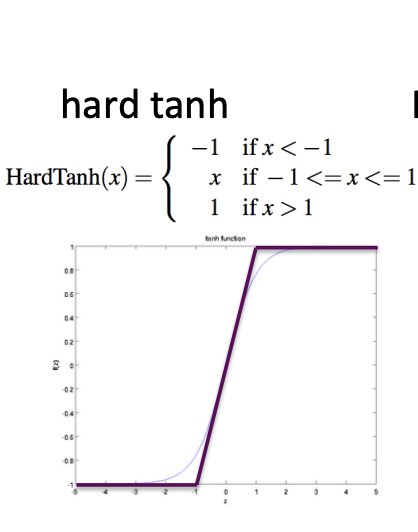
4. ReLU

Deep network를 만들기 위해서는 ReLU를 먼저 사용한다.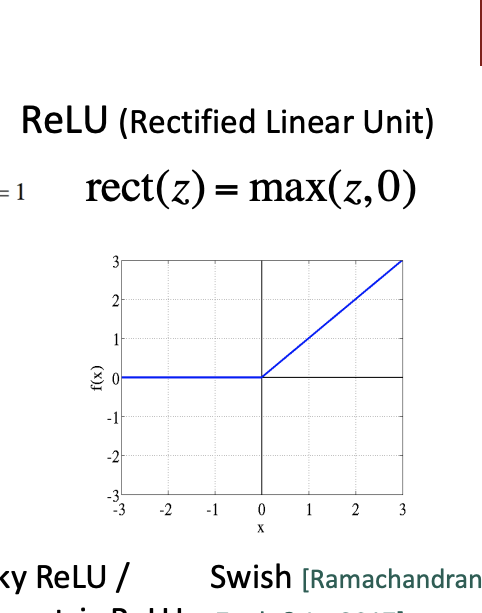

이 함수는 좋은 gradient backflow로 인해 빠르고 성능이 좋다고 한다. 0보다 작은 경우는 0이고 0이상인 경우는 입력값과 동일한 결과값을 출력한다.

parameter Initialization

매개변수를 초기화한다.

• 보통 작은 랜덤한 값들로 weight를 초기화한다.
• hidden layers의 편향값은 0으로 초기화한다. 결과 편향값은 최적값으로 초기화한다. (만약 weight가 0이라면)
• 모든 다른 가중치 또한 초기화한다. (uniform(-r,r)를 사용하여 너무 크거나 너무 작지않게 한다)

Optimizers

보통 확률적 경사하강법은 잘 실행된다.

하지만 좋은 결과를 얻기 위해서는 adaptive한 optimizers가 필요하다.

예를 들면,

• Adagrad
• RMSprop
• Adam
• SparseAdam

등등이 있다.

Learning Rates

단순 확률적 경사 하강법을 사용하는 경우 학습률을 선택해야한다.

학습률을 너무 크게 선택하면 모델이 발산하거나 수렴하지 않을 수 있다. 만약 학습률이 너무 작다면 데드라인까지 모델 학습이 되지 않을 수 있다.

보통은 학습률을 낮추면 더 좋은 결과를 얻는다.

• by hand : 매 k 에폭시마다 학습률을 반으로 줄인다. 데이터 통과를 항상 일정한 순서로 하고 싶지 않기 때문에 매 에폭시마다 데이터를 shuffled한다. 이는 모델이 패턴을 가질 수 있기 때문이다.
• by formula: $lr = lr_0e^(-kt)$라는 공식을 사용한다. t는 에폭시이다.
• fanicer 방법이 더 있지만 (cyclic learnig rate)와 같은,, 하지만 여기서는 다루지 않는다. 최적화가 실행되면서 학습률은 초기보다 더 떨어지기 때문에 처음에는 높은 학습률을 선택한다고 한다.

Language Modeling

이제 재밌는 이야기를 하자.

언어 모델의 과업은 다음 단어가 무엇이 올지 맞추는 것이다.

the students opened their ___

라고 적었을 때, 빈칸에는 books, laptops, exams 등등이 올 수 있다.

각각의 단어를 $x^1, x^2, x^3 ..$라고 할 때,

다음 단어 $x^(t+1)$의 확률분포는

$P(x^(t+1) | x^t, ,,, x^1)$이 된다.

더 쉽게 예를 들면

the students opened

에서의 확률은

the 단어의 확률 the 다음 students가 올 확률 the 다음 students 다음 opened가 올 확률

로 구할 수 있다.

이를 수식으로 구하면

이렇게 곱으로 확률을 나타낸다.

n-gram Lanuage Models

단순한 언어 모델이다

맨 처음 Markow 추정을 통해 계산해보면

추정은 분모를 n-1그램의 확률, 분자는 n 그램의 확률로 계산한다.

그럼 어떻게 확률을 구하는가? 에 대한 답은 text에서 개수를 세는 것이다.

만약 4-gram 언어모델을 예로 들어서

as the proctor started the clock, the students opened their _

라는 문장이 있다면 마지막 3개의 단어를 제외하고 모두 삭제한다.

as the proctor started the clock, the students opened their _

그 다음 분모는 'students opened their'의 문장의 개수가 되고 분자는 'students opened their w'의 문장의 개수가 된다.

예를 들어 'students opened their'의 문장의 개수가 1000개이고
'students opened their books'의 문장의 개수가 400개이면 확률은 0.4가 되는 것이다.

이런 방법에는 문제점들이 있다.

Sparsity Problems

일단 만약에 분자의 데이터의 개수가 너무 작으면? 어쩌나?

여기서는 약간의 델타값을 모든 단어에 추가한다. 이를 smoothing이라고 한다.

만약 분모에 들어갈 개수가 작으면? 0이면? 사실 더 큰일인 문제이다. 이때는 'students opened their'의 문장의 개수가 아닌 'opened their'의 문장의 개수를 대신하여 사용한다. 이를 backoff라고 한다.

여기서 n이 커질수록 sparsity 문제 또한 커진다는 걸 알 수 있다. 즉 더 많은 데이터가 필요하게 된다.

Storage Problems

모델이 저장할 공간이 없다.
모든 n-grams에 대한 개수를 저장해야한다.

만약 코퍼스나 n이 증가한다면 모델의 사이즈 또한 증가하게 된다.

n-gram Language Models in practice

연습삼아 하나를 샘플링해보자.

만약 자신의 노트북에 1.7million word corpus가 있다고 하자.

today the ____

의 빈칸에 확률분포가 다음과 같다고 한다.

company 0.153
bank 0.153
price 0.077
italian 0.039
emirate 0.039

여기서 price를 선택했다고 하자

today the price ____

그럼 다음 빈칸에 대한 확률 분포를 또 구하고 위 과정을 수행하고.. 반복하면..

today the price of gold per ton , while production of shoe
lasts and shoe industry , the bank intervened just after it
considered and rejected an imf demand to rebuild depleted
european stocks , sept 30 end primary 76 cts a share .

꽤 괜찮은 문법인 문장이 완성된다.

하지만 일관성이 없고 의미가 없는 문장이다.

그러면 우리는 의미가 있는 문장을 만들기 위해서 neural Language Model을 만들어보자.

여기서 우리는 window-based neural model을 먼저 생각해보자.

fixed - window neural Language Model

1. words/one-hot vectors
   고정된 윈도우를 사용한다.
   그리고 각각의 단어에 대한 벡터를 만든다.
   여기서는 비슷한 의미의 단어 벡터는 비슷한 벡터를 가진다.
   즉 pupils는 students와 비슷한 의미이기 때문에 students와 비슷한 벡터를 가진다.

2. concatenated word embeddings
   그리고 각각의 단어 임베딩을 모두 더한다.

3. hidden layer
   그리고 히든 함수를 사용한다.

4. output distribution
   그리고 소프트맥스 함수를 통해 결과를 확인한다.

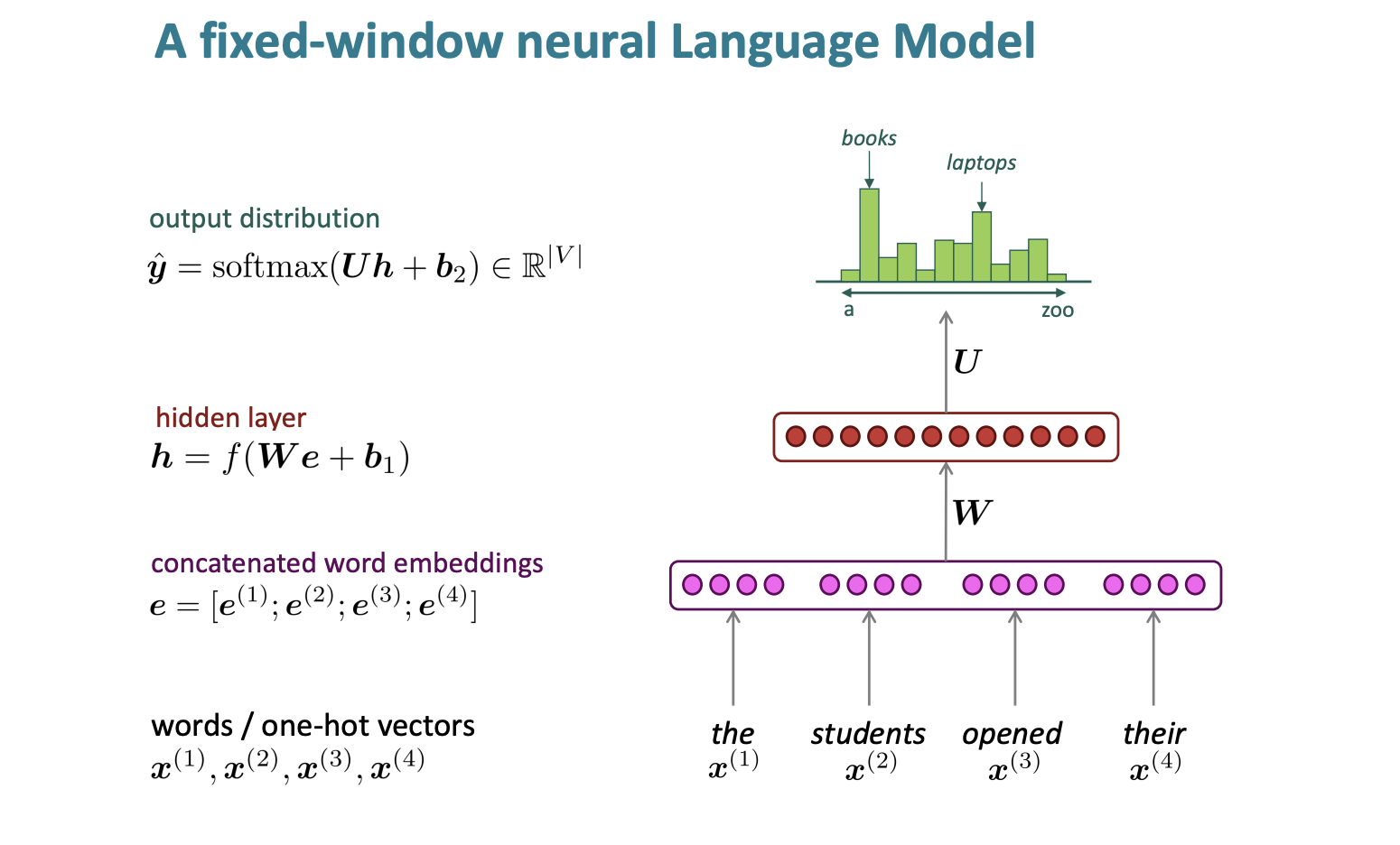
이는 장단점이 있다.

우선 장점

• 희소성 문제가 사라졌다. 텍스트에 없는 단어도 우선 다른 비슷한 단어를 찾아 벡터로 나타나기 때문에 없는 단어에 대한 문제가 사라졌다.
• 모든 n-grams에 대한 저장을 하지 않아도 된다.

단점으로는

• 고정된 윈도우가 너무 작다.
• window를 크게 한다 해도 충분히 크게할 수 없다. 왜냐하면 window를 크게할수록 W 행렬의 크기도 커진다.

즉 우리는 임의의 양의 컨텍스트를 처리하고 매개변수를 더많이 공유하며 근접성에 민감한 모델을 만들어야 한다.
이를 해결하는 것이 바로 RNN이다.

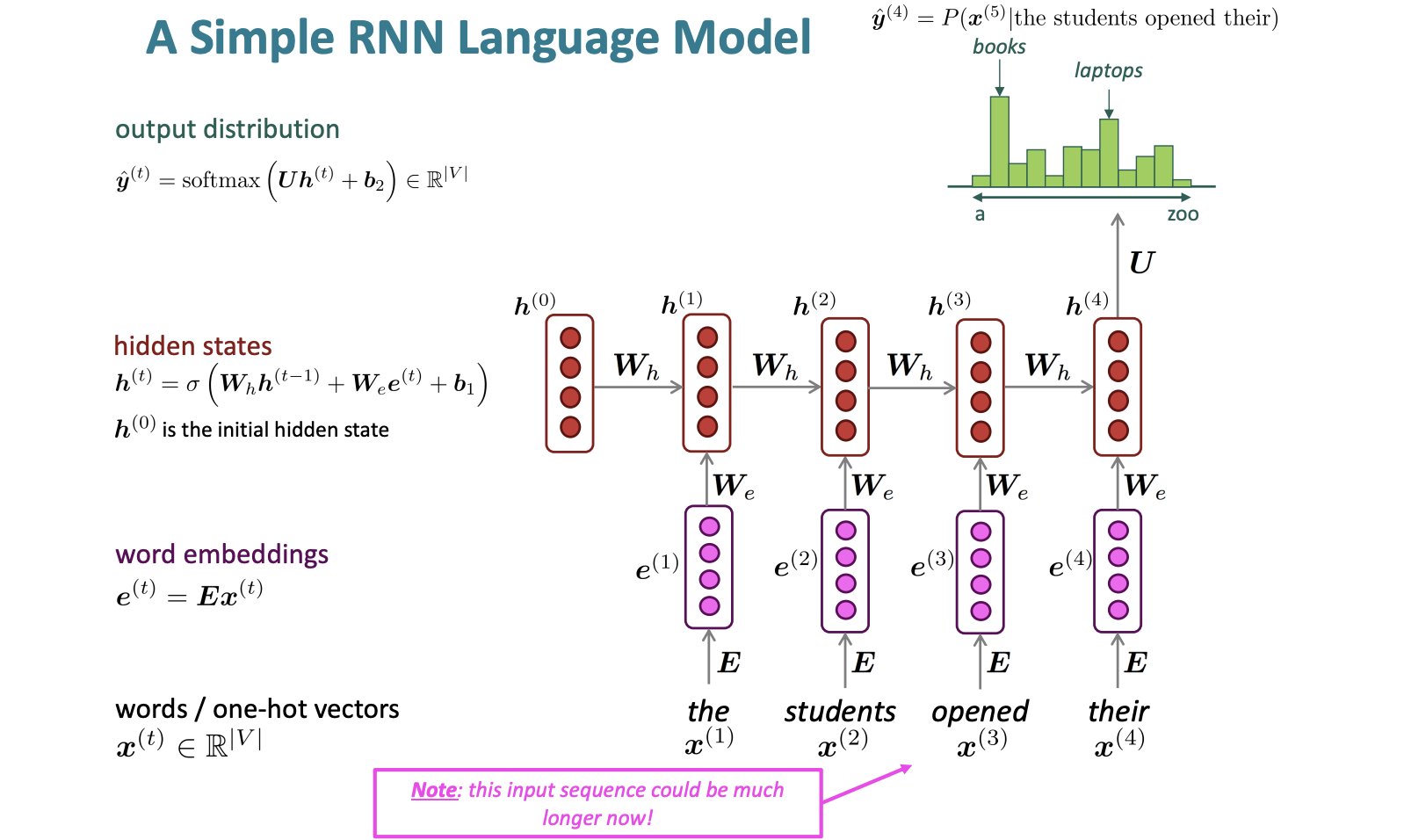
RNN

Recurrent Neural Network는 이름 그대로 히든 레이어를 그 자체로 다시 공급하는 것이다.

그림을 살펴보면,
맨처음 $h^0$ 은 0벡터로 초기화한 것이고 이를 $W_h$행렬을 곱한다.
그리고 맨 처음 단어의 벡터에서 E를 곱한 벡터에 $W_e$행렬을 곱한뒤 둘을 더한다. (bias 도 더한다.) 이 값이 바로 $h^1$가 된다.

여기까지 5강의 내용이었고 이어서 6강을 정리해보자.

Lecture 6

6강의 강의 내용은 다음과 같다.

1. RNN Language Models
2. Other uses of RNNs
3. Exploding and vanishing gradients
4. LSTMs
5. Bidirectional RNNs

저번시간까지 우리는 n-gram language models와 Recurrent Neura Networks에 대해 알아보았다.

오늘은 RNN의 학습방법과 사용법, 문제점에 대해 알아보자.

RNN Language Models

RNN 언어 모델은 어떻게 학습을 할까?

Training a RNN Language Models

• 큰 코퍼스를 얻는다. 일단 일련의 단어들 x1, x2, ..., xT로 구성되어 있다.
• RNN의 입력값으로 준다. 그리고 매 단계 t마다 결과 분포 $\hat{y}^(t)$ 를 계산한다.
• 교차 엔트로피를 사용해서 각 스텝 t마다의 예상되는 확률 분포 $\hat{y}^(t)$ 와 진짜 다음 단어 $y^(t)$에 대해 손실함수를 적용한다.
• 그리고 모든 손실에 대해 평균을 적용한다.
  

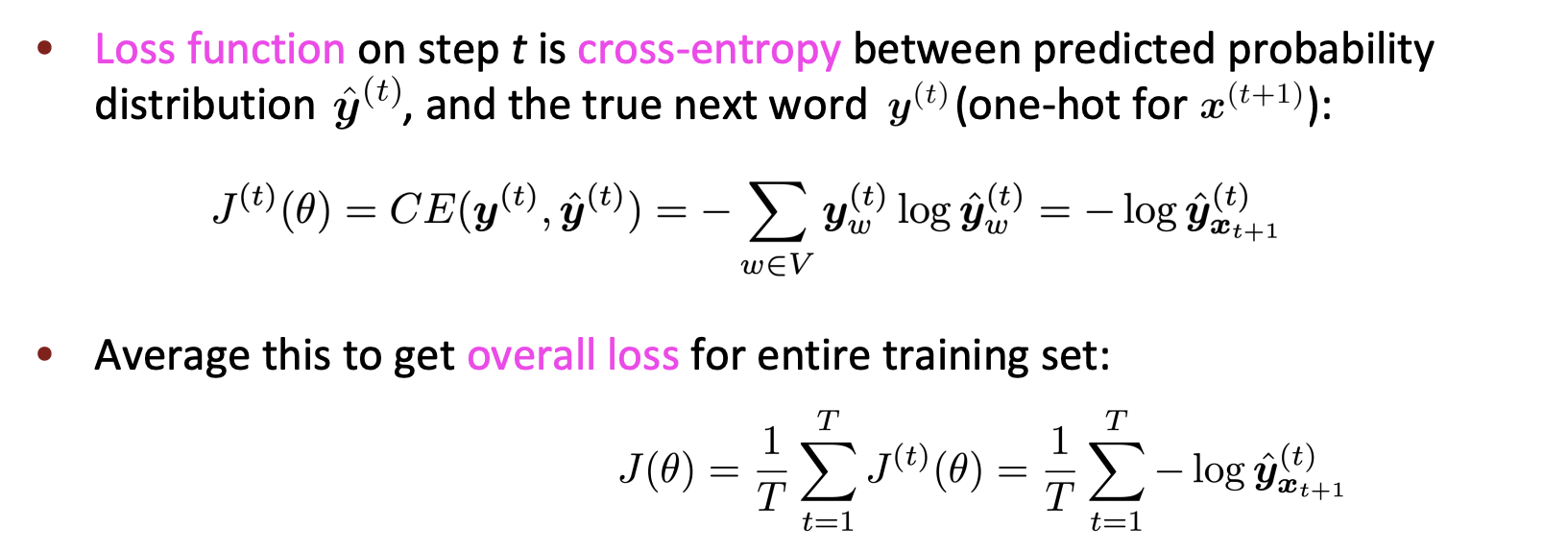
그러니까 일단 우리한테

the students opened their exams

라는 문장이 있다면,
t가 1일 때 단어는 the 라고 하자.

그럼 계산된 $\hat{y}^(1)$은 'predicted prob dists'가 된다. 이 값과 다음 실제 단어인 'students'를 비교하여 Loss인 $J^(1)(\theta)$를 구하는 것이다.

그 다음 단어인 students의 예측 분포와 opened도 마찬가지이다.

이렇게 계속 손실을 구한 뒤 모두 더해서 평균을 구한다.

하지만 이렇게 RNN 언어 모델을 학습하는 것도 단점이 존재한다.
전체 코퍼스에 대해 계산을 각각 진행하여 손실과 미분을 구하는 건 너무 expensive하다.

그래서 문장 또는 문서 단위로 고려하거나
SGD(확률적 경사 하강법)을 통해 최적화를 진행한다.

Training the parameters of RNNs

그럼 질문 하나.

반복되는 행렬인 $W_h$ 에 대한 $J^(t)(\theta)$의 미분값은 무엇인가?
바로 각각의 시간동안 나타나는 Wh에 대한 미분의 합이다.

왜?

우리는 3강에서 체인 규칙에 대해 배웠다.

다변량 함수인 f(x,y)에 대해 x(t), y(t)가 주어진다면

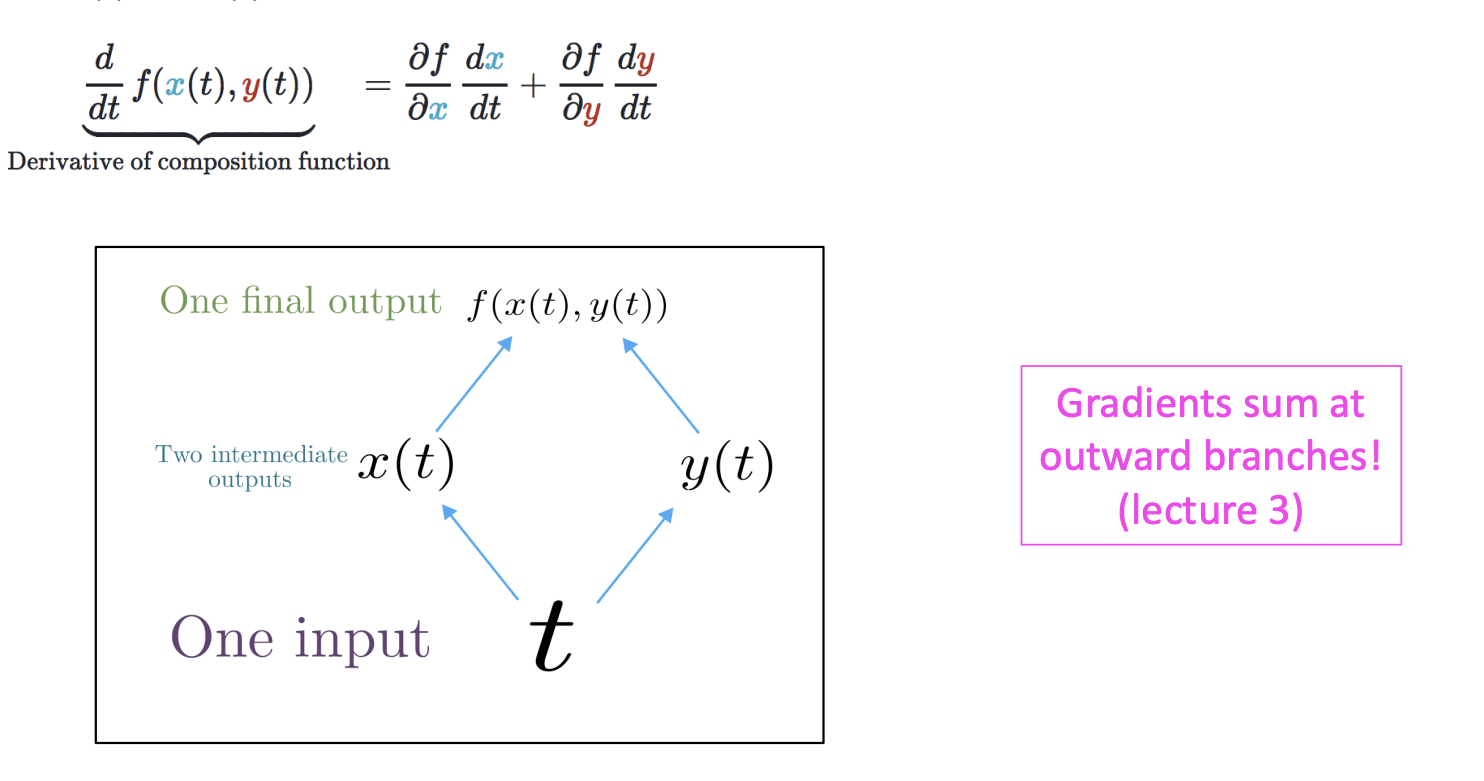
체인 규칙을 통해 미분 값을 위처럼 구할 수 있다.

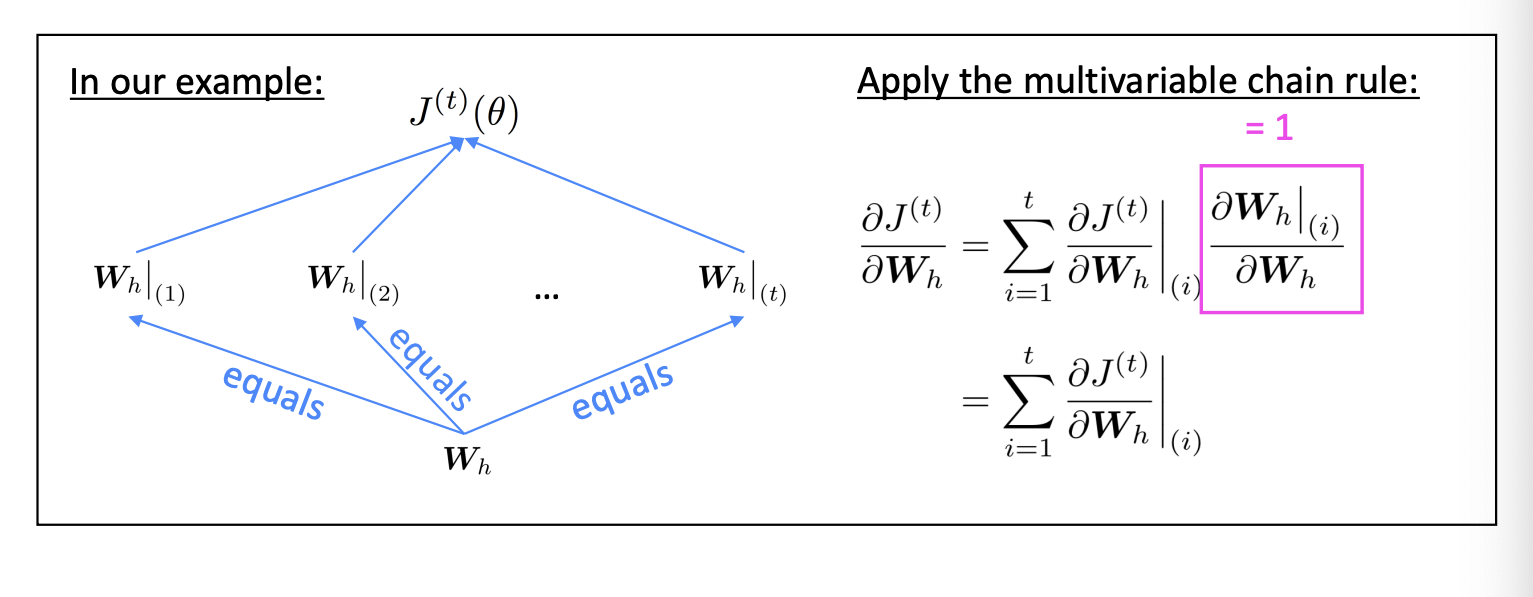
이러한 이유로 각 Wh에 대해 미분한 값을 모두 더하는 것이구나~

Backpropagation for RNNs

그럼 위 값을 어떻게 계산할까?

Backpropagation을 통해 계산하면 된다.
이를 시간에 따른 역전파 "backpropagation through time"이라고 한다.

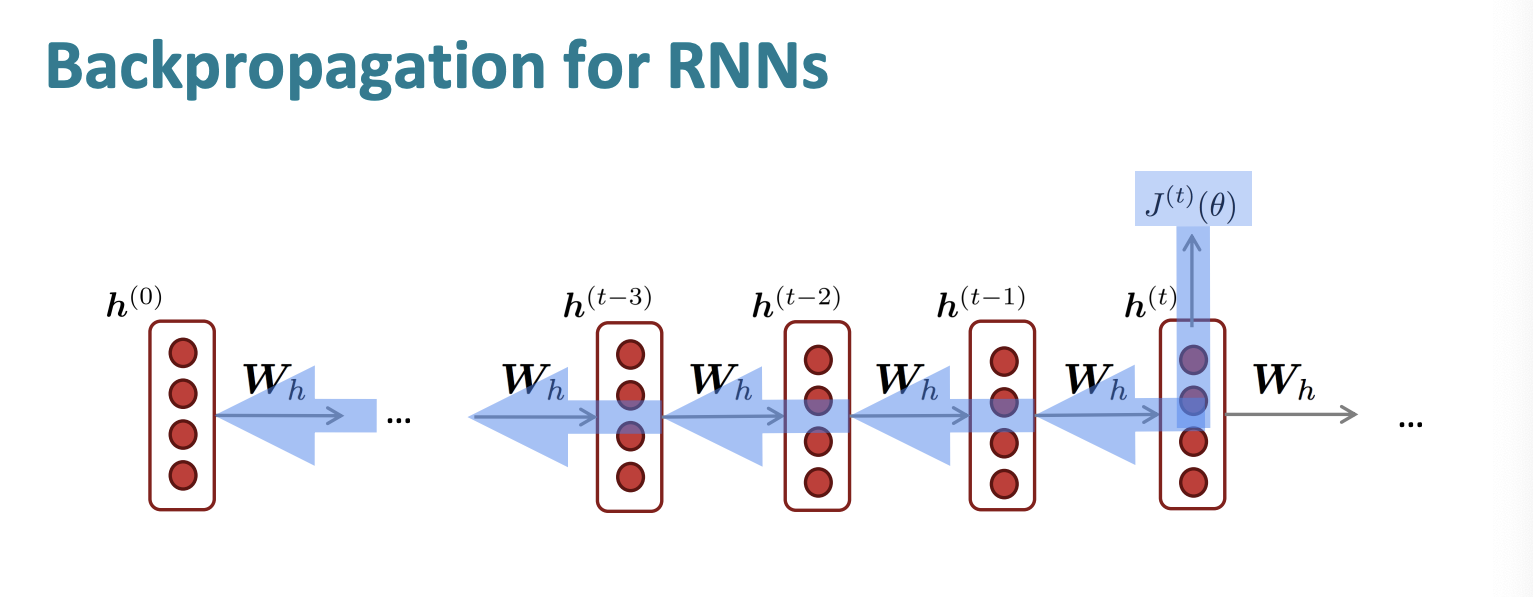
긴 문장에 대해서 실행한다면 속도가 엄청 느릴 수 있다. 따라서 시간을 예를 들어 20이라고 설정하고 20개의 시간 단계 동안만 실행하고 합산할 수도 있다.

Generating text

저번 n-gram처럼 출력 단어를 다시 입력으로 넣어 문장을 출력한다.
해리포터 또는 요리책을 입력으로 받아 문자를 출력할 수 있다.

결과적으로는 내용상 아직 일관성이 없어 텅 빈 강정 같은 느낌인데, 그래도 문법이나 출력 형식의 경우 상당히 성능이 있음을 보였다.

Evaluating Language Models

그럼 모델이 좋은지 나쁜지 어떻게 평가할까?

우리는 perplexity 한국어로 당혹감를 통해 언어 모델을 평가한다.

당혹감은 위처럼 계산한다.
예를 들어 김치에 대해 이야기하다가 갑자기 학교! 단어 또는 내용이 나오면 당혹스러울 수 있다. 이를 수식으로 표현한 것이다.

즉 낮은 perplexity가 좋은 성능인 것이다.
이는 loss J에 대한 지수승으로도 표현 가능하다.

n-gram model에 대한 perplexity는 굉장히 높았다. 하지만 계속 꾸준히 연구한 결과 67.6 까지 낮췄다.
하지만 RNNs 이 발전하면서 최고 30까지 perplexity를 낮출 수 있었다.

Why should we care about LM?

우리가 언어 모델에 대해서 생각해보아야할 것이 무엇이 있을까?

• Predictive typing
• Speech recognition
• Handwriting recognition
• Spelling/grammar correction
• Authorship identification
• Machine translation
• Summarization
• Dialogue
• etc.

그럼 RNN이 언어 모델인가?

RNN != Language Model 이다.

Other uses of RNNs

다른 용도로 RNN을 이용할 수 있다.

part-of-speech tagging, sentiment classification, question answering, speech recognition, machine traslation 에 대해서도 이용할 수 있다.

감정 분석은 마지막 히든 state만 사용하는 것보다 전체 state에 대해 평균을 내거나 max를 구하는 경우에 더욱 usually better하다.

그리고 답변을 하는 경우에는 RNN은 encoder같은 역할을 하게 된다.
이러한 자세한 내용들은 지금은 다루지 않겠다.

Exploding and vanishing gradients

그럼 우리는 지금 RNN에 대해 배웠는데, 단점이 없을까?

있다. 첫번째 단점은 gradients가 사라지는 문제이다.

Vanishing gradients

이를 Vanishing gradient이라고도 한다.
그럼 직관적으로 어떻게 문제가 발생하는지 보자.

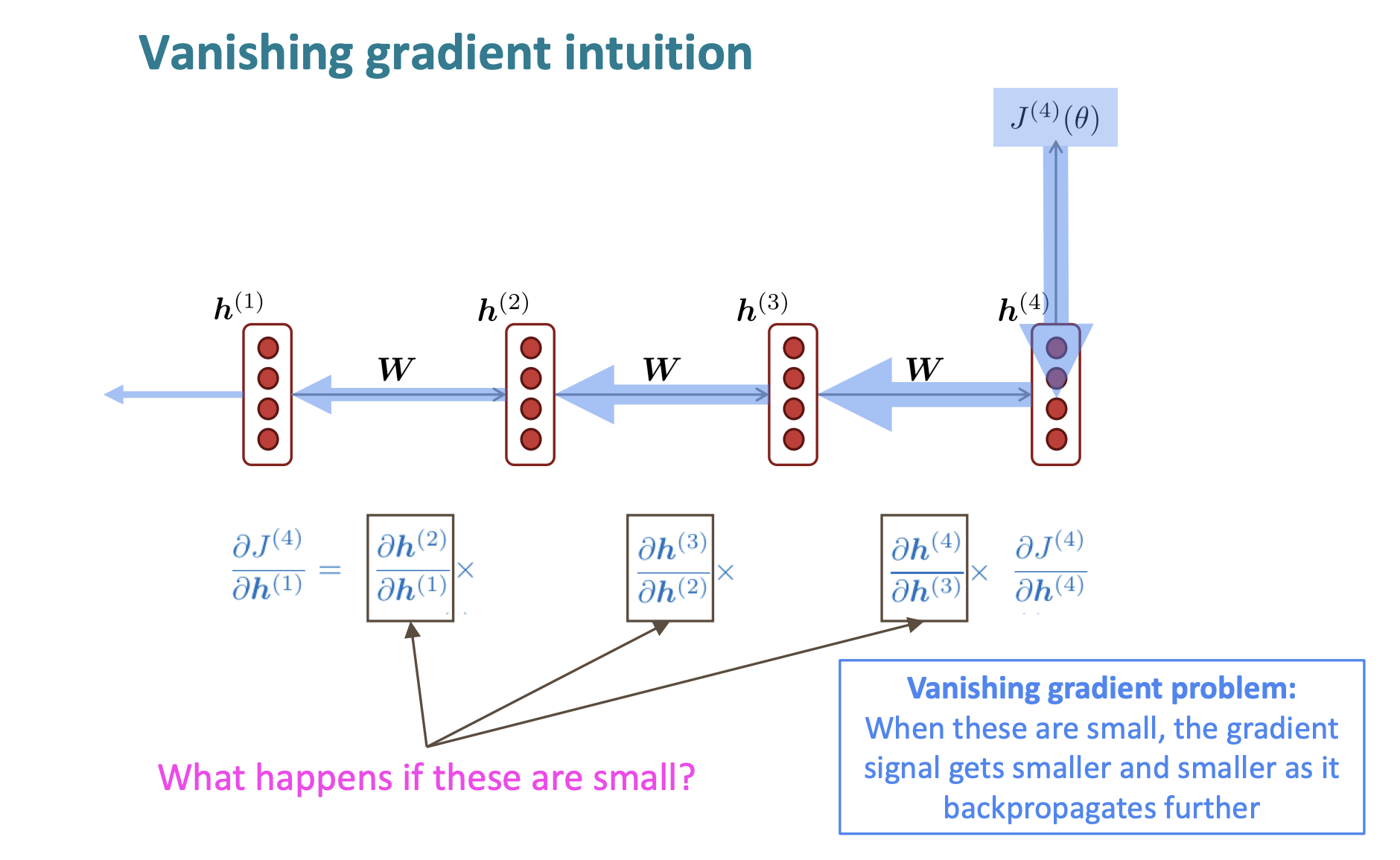
자 우리가 $J^4$ 를 $h^1$에 대해 미분한 결과는 위처럼 구할 수 있다.
만약 next hidden state를 previous hidden state로 나눈 결과가 매우 작다면? 바로 Vanishing gradient problem이 발생한다.

아니 왜?

한번 간단하게 선형 case에서 증명해보자.

우리는 hidden state를 다음과 같은 식으로 표현했다.

$h^(t) = \sigma(W_hh^{(t-1)} + W_xx^{t} + b_1)$

그럼 만약 $\sigma$ = x 라고 하면? 항등 함수가 된다.

가 된다. (수식 적기 너무 빡세다;)

그럼 우리는 step i에 대한 loss $J^i(\theta)$ 를 hidden state $h^j$에 대해 미분한 것을 알아보자. 그리고 $l = i - j$라고 하자.

자 일단 체인 규칙으로 인해서 첫번째 수식은 이해할 수 있따.
그리고 아까 구한 식으로 $W_h$로 나타낼 수 있따. 이는 i와 상관없기 때문에 l만큼 반복되어 l승으로 표현할 수 있다.

만약 $W_h$가 너무 작으면 현재 i 스텝에서 이전 j 스텝에 대한 미분은 거의 소멸하는 것이다.

그럼 $W_h$가 작은 것은 무엇을 기준으로 이야기를 하는 것인가?

바로 $W_h$ 행렬의 고유값들이 모두 1보다 작을 때를 이야기한다.

행렬 미분을 위같은 수식으로 나타낼 수 있다. (사실 왜 저 수식이 성립하는 지는 정확히 모르겠다.) 하지만 저 수식이 참이라면, 고유값이 1보다 작을 때 l이 커지면 커질 수록 미분값은 매우 작아짐을 의미한다.

정확한 증명은 논문을 직접 참고하자.

"On the difficulty of training recurrent neural networks”, Pascanu et al, 2013. http://proceedings.mlr.press/v28/pascanu13.pdf
(and supplemental materials), at http://proceedings.mlr.press/v28/pascanu13-supp.pdf

지금까지 직접 미분 신호는 거리가 멀어질 수록 사라지는 것을 확인했다.
이것은 무엇을 의미하는가?

바로 model의 weight는 주변 효과에 대해서만 업데이트 된다는 것을 의미한다. 즉 장기적인 효과를 가질 수 없다는 것이다.

다음과 같은 문장이 있고 빈칸을 꾸며야하는 작업을 수행한다고 하자.

LM task: When she tried to print her tickets, she found that the printer was out of toner.
She went to the stationery store to buy more toner. It was very overpriced. After
installing the toner into the printer, she finally printed her ____

우리는 쉽게 빈칸에 tickets가 들어가는 것을 찾을 수 있지만, RNN 모델은 장기기억을 하지 못하기 때문에 빈칸을 유추하기가 사실 상 어렵다.

지금까지 Vanishing gradients 문제를 알아보았다.

Exploding gradient

그럼 Exploding gradient는 무슨 문제일까?

만약 gradient가 엄청 크면 무슨일이 발생할까?

우리는 SGD를 통해 새로운 $\theta$값을 가진다.

$\theta^{new} = \theta^{old} - \alpha \nabla_\theta J(\theta)$

이는 엄청 큰 step을 가지게 된다.
즉 의도치않은 큰 발자국을 가지게 되는 것이라서 쉽게 최적화된 값을 구할 수 없다는 것이다.

이는 무한대로 발산할 가능성이 있으며 또는 NaN 값을 얻을 수 있다.

그러하면, 이 문제를 해결할 방법은?

바로 Gradient clipping이다.

어떠한 한계점보다 gradient 절대값이 크게되면, 이전 SGD 업데이트에서 크기값을 조정하는 것이다. (방향은 동일하지만 크기만 조절한다.)

Exploding gradients 문제는 비교적 쉽게 해결할 수 있기 때문에 Gradient clipping은 굉장히 중요하다.

그러면 Vanishing Gradients는 어떻게 해결하지?

많은 시간이 지난 정보를 보존하는 것은 굉장히 어려운 문제가 되었다.
그럼 separate 한 memory를 가지는 것을 어떻게 할까?

이를 해결하는 것이 바로 LSTMs이다.

LSTM

Long Short-Term Memory RNNs 의 약어이다.

step t에는 hidden state h와 cell state인 c가 존재한다.

• 둘다 벡터 길이는 n이다.
• cell은 long-term 정보를 저장한다.
• LSTM은 셀에서부터 정보를 읽거나 지우거나 쓰는것이 가능하다.

지우거나 쓰거나 읽거나 이 셋중 하나의 선택은 gates에 듸해 선택된다.

• 각 게이트들은 n 길이의 벡터를 가진다.
• 각 시간마다 각각의 게이트들은 1(open) 또는 0(closed)값을 가지거나 그 두 사이의 값을 가진다.
• 게이트들은 동적이다.

각 게이트에 대해 알아보자.

• Forget gate: 이전 cell state로부터 유지할지, 아님 잊어버릴지 조절한다. (0,1)의 출력값을 가지고 1에 가까울 수록 더 많이 기억한다.
  - $f^t = \sigma(W_f h^{t-1} + U_f x^t + b_f)$
• Input gate : 현재 정보를 기억하기 위해 만들었고 0과 1의 출력값을 가지며 1에 가까울 수록 현재 정보를 더 많이 기억하는 것이다.
  - $i^t = \sigma(W_i h^{t-1} + U_i x^t + b_i)$
• Output gate : cell의 부분을 hidden state에 보낼지 말지 조절한다. 새로운 hidden vector를 결정하게 된다. (0,1)의 값을 가지며 1에 가까울 수록 새로운 상태 부분을 활용하게 된다.
  - $o^t = \sigma(W_o h^{t-1} + U_o x^t + b_o)$

그러면 새로운 cell content 가 뭘까?

$\widetilde{c}^t = tanh(W_c h^{t-1} + U_c x^t + b_c)$

tanh에 의해 출력을 생성한다. tanh 특성상 값의 범위는 (-1, 1)이다.

Cell state는 이전 cell에서 몇개의 content를 지우고 새로운 셀의 내용을 적는다.

Hidden state는 셀에서부터 몇개의 내용을 읽는다.

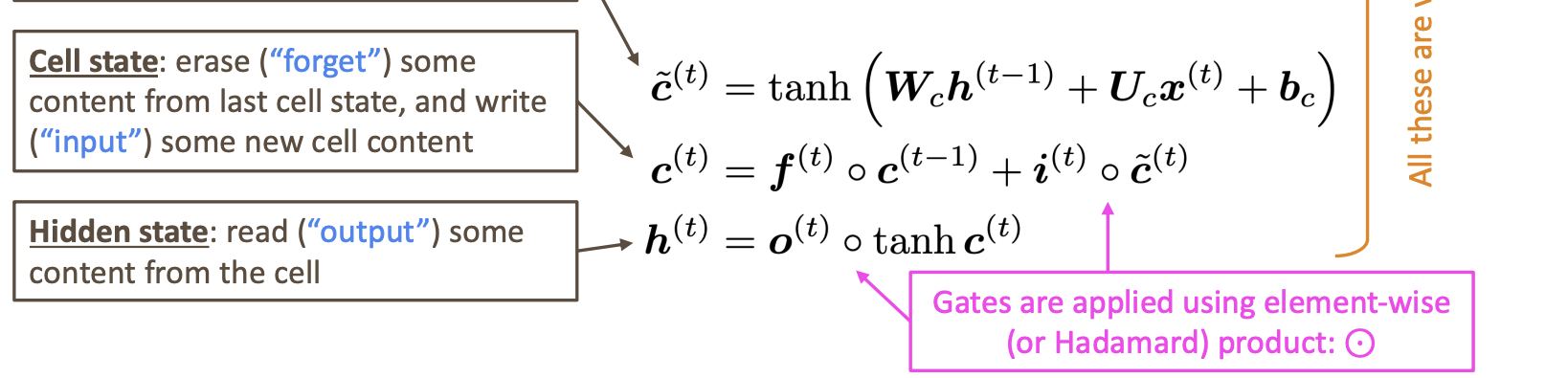
LSTM의 그림

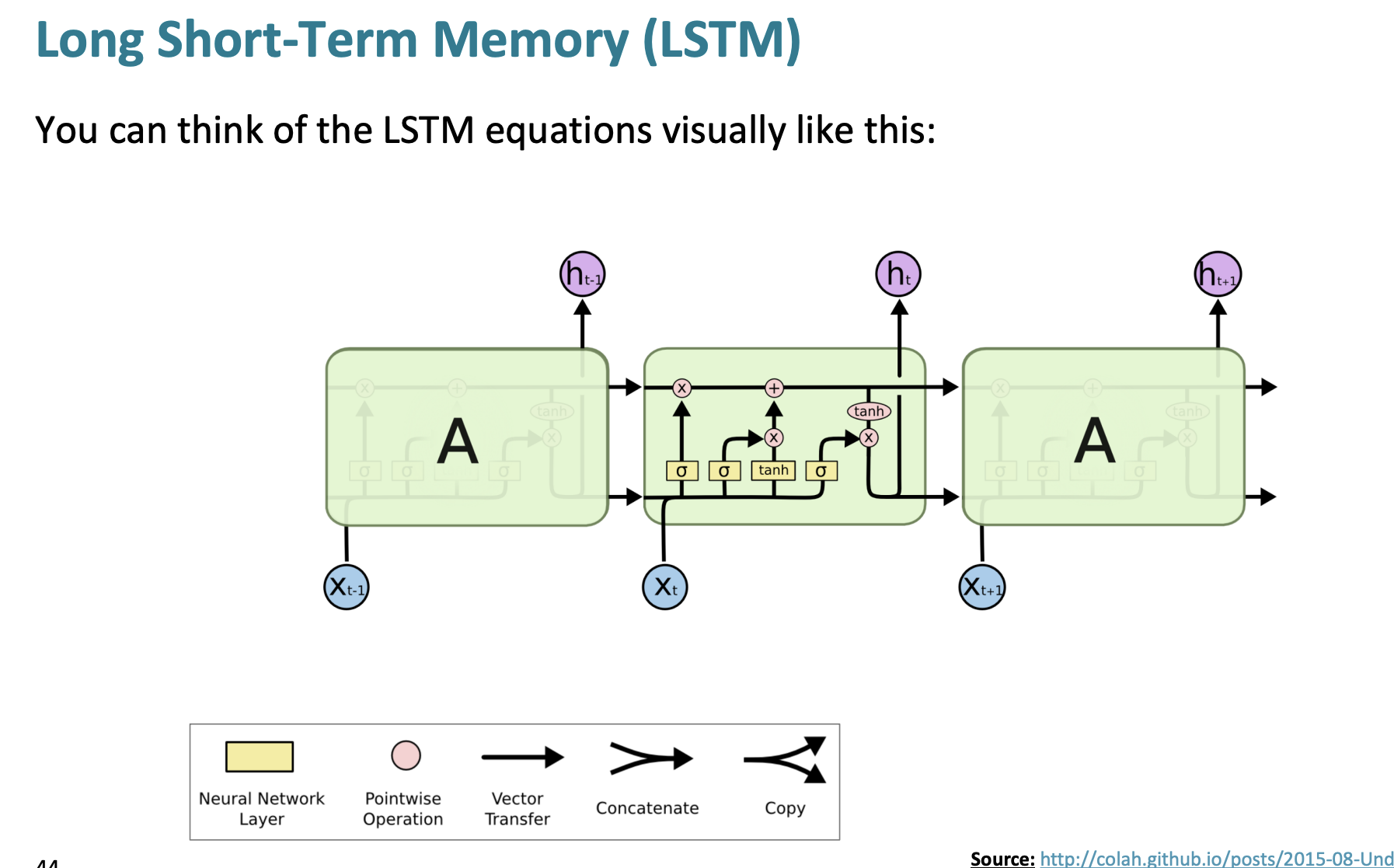
LSTM은 위처럼 생겼다.

더 자세히 살펴보자.

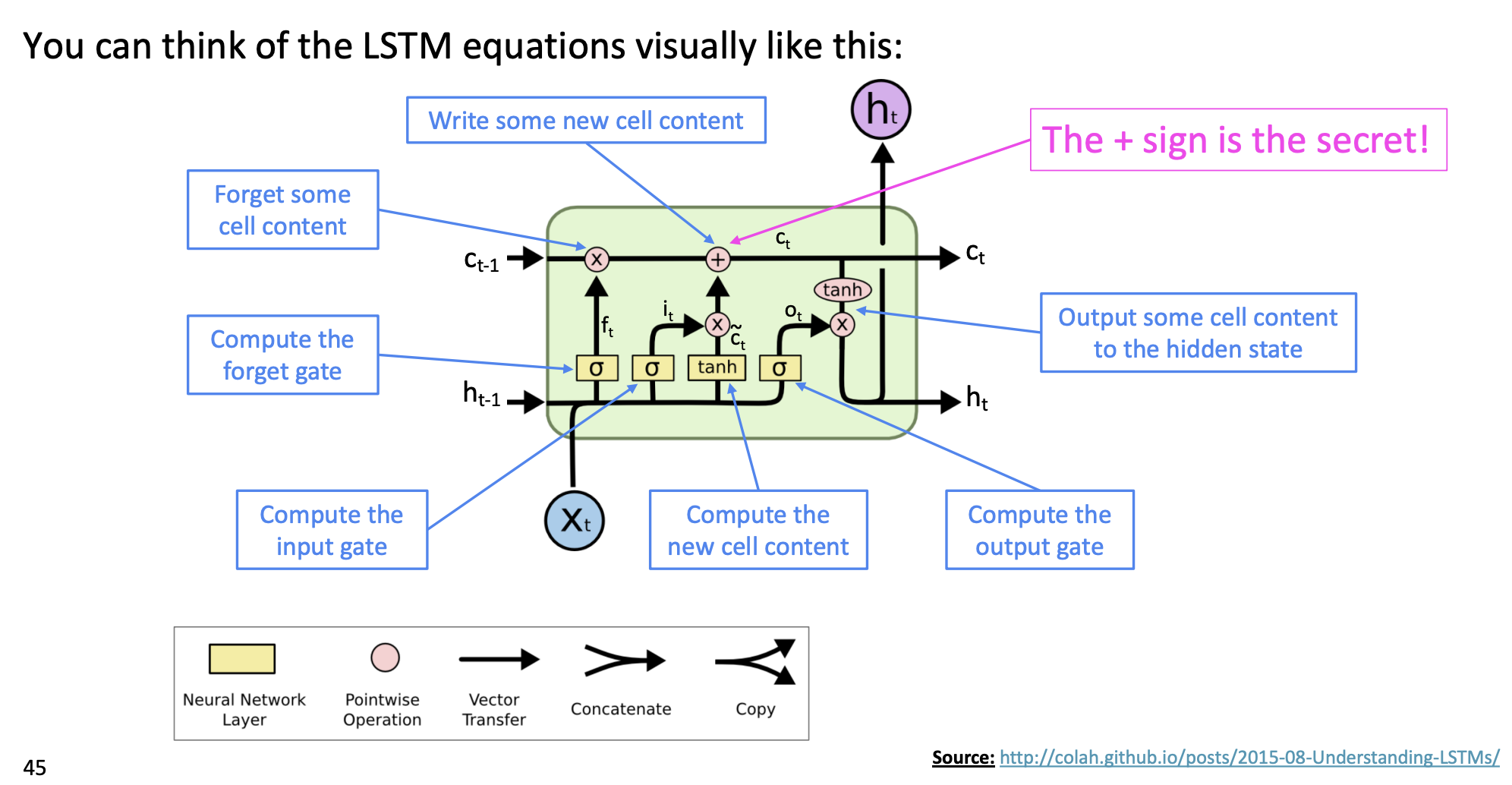
맨 왼쪽에 f (망각 게이트)를 보면 이전 내용을 얼마나 망각할지 정한다.

중간에는 새로운 내용인 $\widetilde{c}^t$에 input gate가 이전 내용을 얼마나 저장할지 보여주고 있다.

수식과 위 그림을 자세히 보면 이해를 쉽게할 수 있다.

실제로 LSTM은 2013-2015년에 성공했다는 것을 알 수 있고,

현재 접근으로는 변압기와 같은 새로운 접근들이 더 우세하다.

vanishing/ exploding gradients 문제가 단순히 RNN의 문제일까?

아니다. 이건 모든 신경 아키텍쳐의 문제이다.

이러한 모든 딥 feedforward/ convolutional 아키텍쳐의 해결 방법은 새로운 직선 연결을 추가하는 것이다.

예를 들면 ResNet 같은 것이 있다. (자세한 설명 pass)

또는 DenseNet 같은 것이 있다. (자세한 설명 pass)

결과적으로는 RNN은 같은 weight matrix를 계속 곱해 나가니 부분적으로 불완전한 특징을 가지고 있다.

Bidirectional RNNs

우리가 만약 감정 인식 모델을 만든다고 가정하자.

the movie was terribly exciting !

이라는 문장에서 'terribly' 라는 단어는 어떤 의미로 사용되었나?

여기서 만약 'terribly' 앞까지만 확인한다면 이 단어는 부정적인 의미로도 생각될 수 있다.

하지만 결과적으로 뒤에 'exciting'이 왔기 때문에 긍정적인 단어로 사용되었다.

우리가 지금까지 배운 RNN에서는 뒤에 단어를 확인할 수 없다.
왜냐하면 앞에서부터 점진적으로 행렬 계산이 수행되기 때문이다.

그래서 우리는 양방향 RNN을 만들것이다.

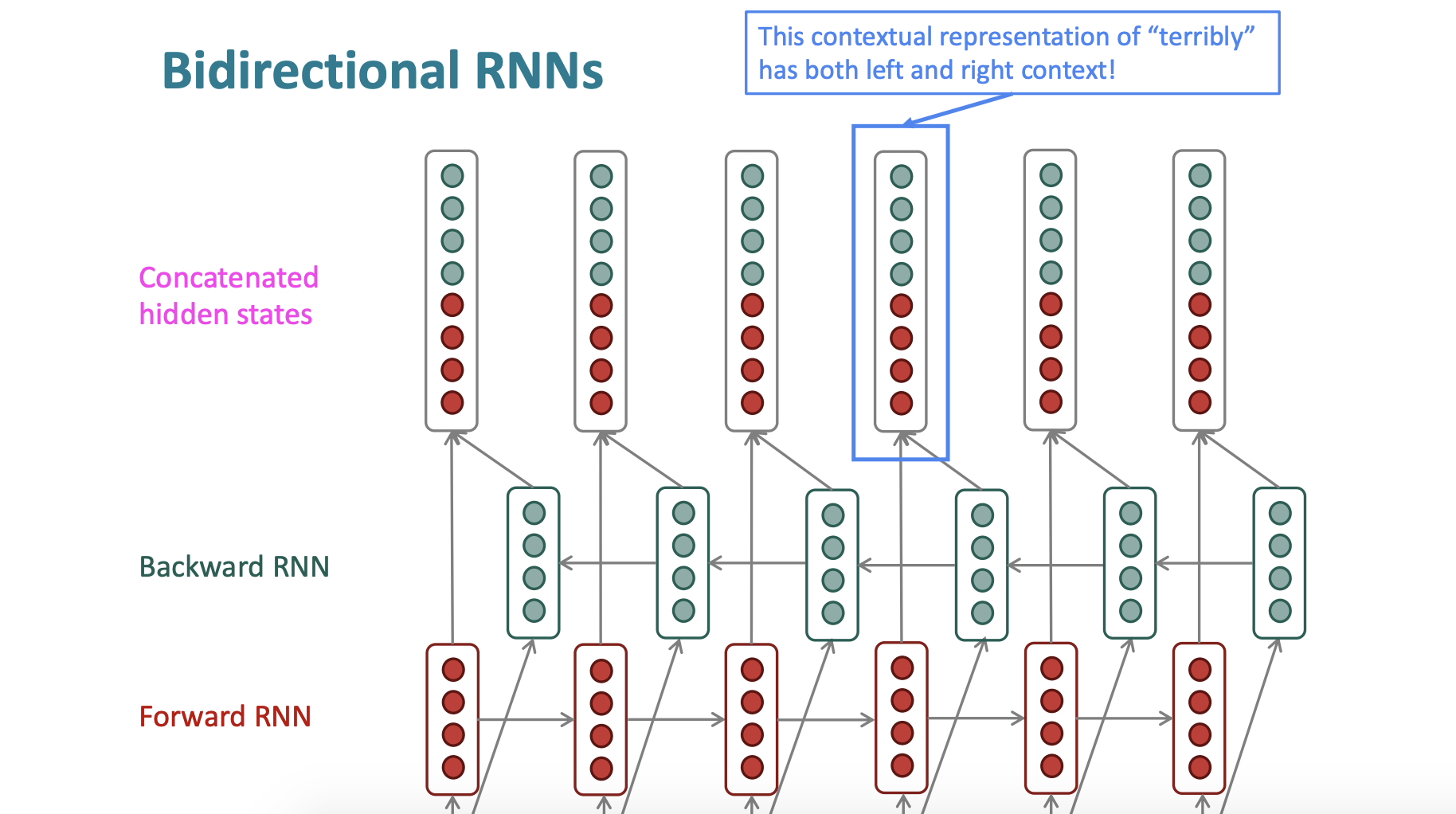
새로운 hidden state를 추가해서 concatenate를 한다.
그러면 이전 state와 다음 state를 합해서 계산을 하게 된다.

그리고 양방향 RNN은 다음과 같이 화살표로 쉽게 표현할 수 있다.

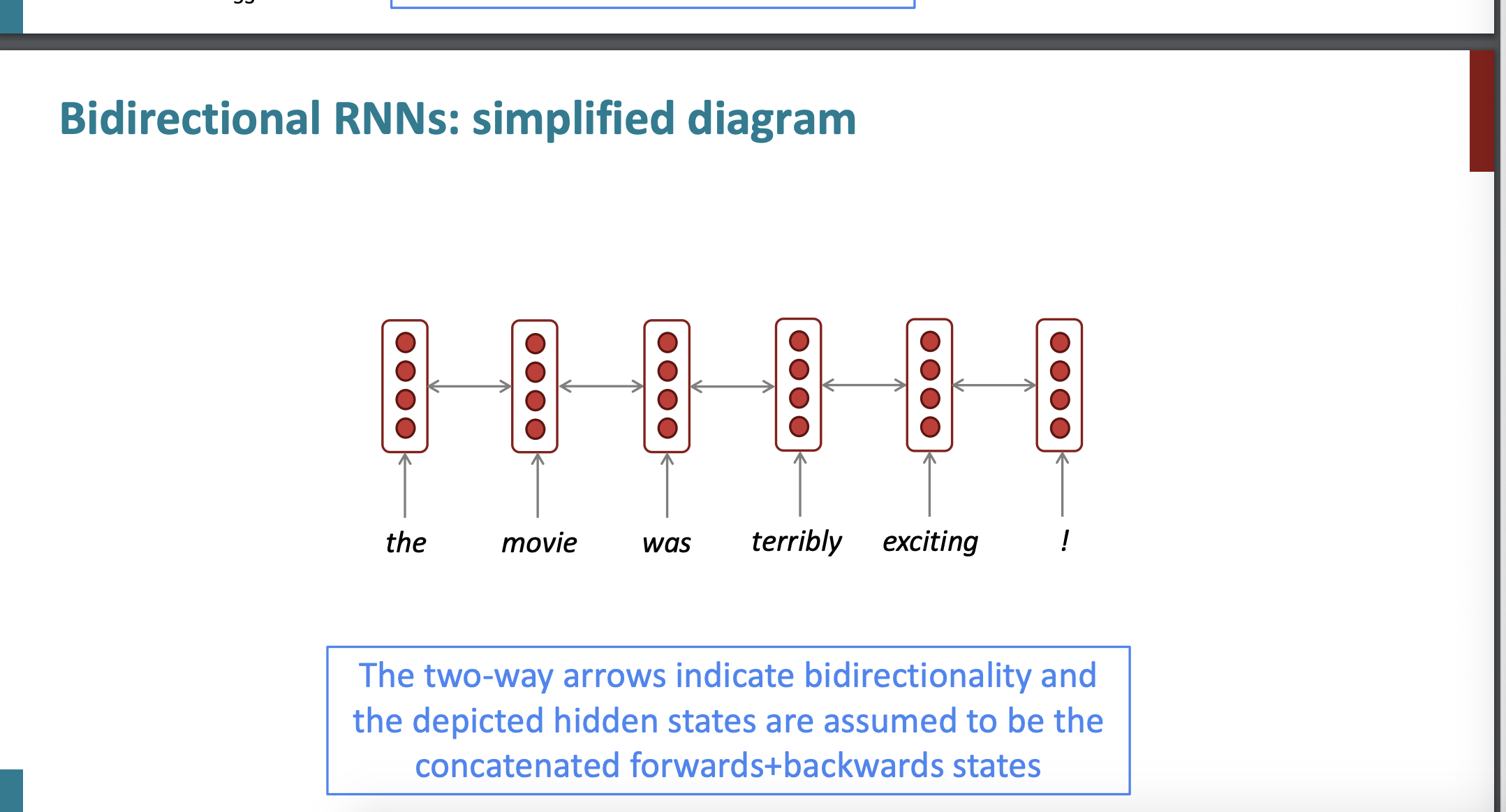
이러한 양방향 RNN은 사실 언어 모델에 적합하지 않다.
언어 모델은 다음 단어를 예측하는 것이 목적인데 다음 단어가 무엇인지 모르는 상태에서 어떻게 hidden state를 만드는가? 불가능하다.

따라서 완전한 전체 input 문장을 넣을 수 있을 때 양방향 RNN이 강력하다.
나중에 배울 BERT(Bidirectional Encoder Representations from Transformers) 또한 양방향으로 설계된 시스템이다.

여기까지 6강 내용이다.