• 참고 자료
  강의영상
  강의자료
  추가노트

Lecture 8

8강부터 2023년 강의 영상으로 공부를 진행하게 되었다.

오늘 배울 내용은

• RNN to attention-based NLP models
• The Transformer model
• Great results with Transformers
• Drawbacks and variants of Transformers

이다.

RNN to attention-based NLP models

저번 강의 시간에는 기계 번역에 대해 배웠다.
기계 번역의 입력문장이 만약 "I like pizza" 라고 하자.
우리는 이미 I 다음 단어가 like 인 것을 알고 있다.

따라서 이 문장을 bidirectional LSTM으로 넣는다.

우리의 출력 문장은 다음 단어가 무엇인지 모른다. 따라서 LSTM으로 출력한다.

저번시간에 배운 attention 으로 유연하게 메모리에 접근할 수 있게된다.

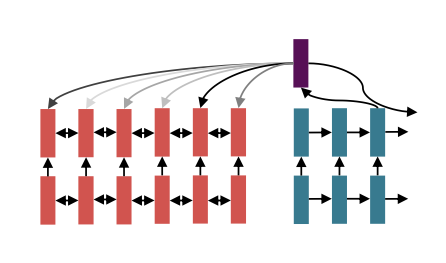
이러한 rcurrent models 구조는 여러 문제가 있다.

Linear interaction distance

• RNN은 왼쪽 -> 오른쪽 구조이다.
• 이는 linear locality 를 가진다. 그러니까 근처에 있는 단어 끼리 상호 연관성을 가진다는 의미이다. 뭐 가끔은 tasty pizza 와 같이 가까이 있는 단어끼리 연관이 있을 수 있지만 항상 그런 것은 아니다.
• 따라서 멀리 있는 단어 끼리의 상호연관성을 가지기 힘들기 때문에 문제가 발생한다.

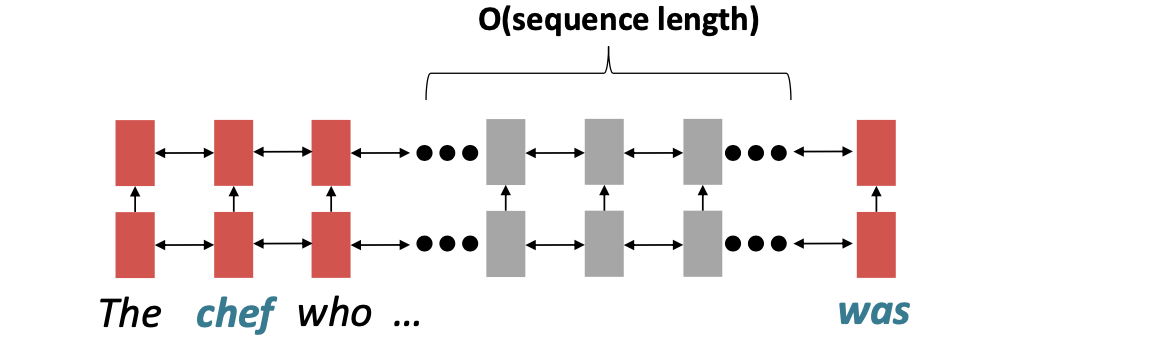
chef 와 was는 O(sequence length) 만큼의 시간이 걸린다.

Lack of parallelizability

Forward 와 Backward pass 모두 O(sequence length) 만큼의 비병렬성 시간이 걸린다.

GPU는 많은 독립적인 일들을 한번에 처리할 수 있다.
하지만 미래의 RNN hidden state는 이전 RNN hidden state를 모르면 계산할 수 없다.
따라서 시간상 매우 비효율적인 것이다.

Attention

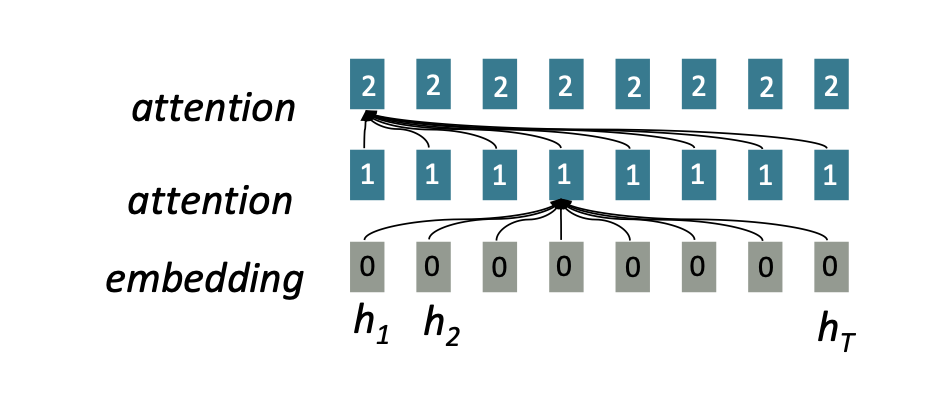
어텐션은 각각의 단어 표현을 query로 다루어 각 집합에 접근하고 값 집합의 정보를 통합한다. 이전에 RNN의 구조에서는 상호작용 거리가 O(N)이었다면 이번에는 O(1)이다. 왜냐하면 모든 단어가 모든 계층에서 상호작용하기 때문이다.

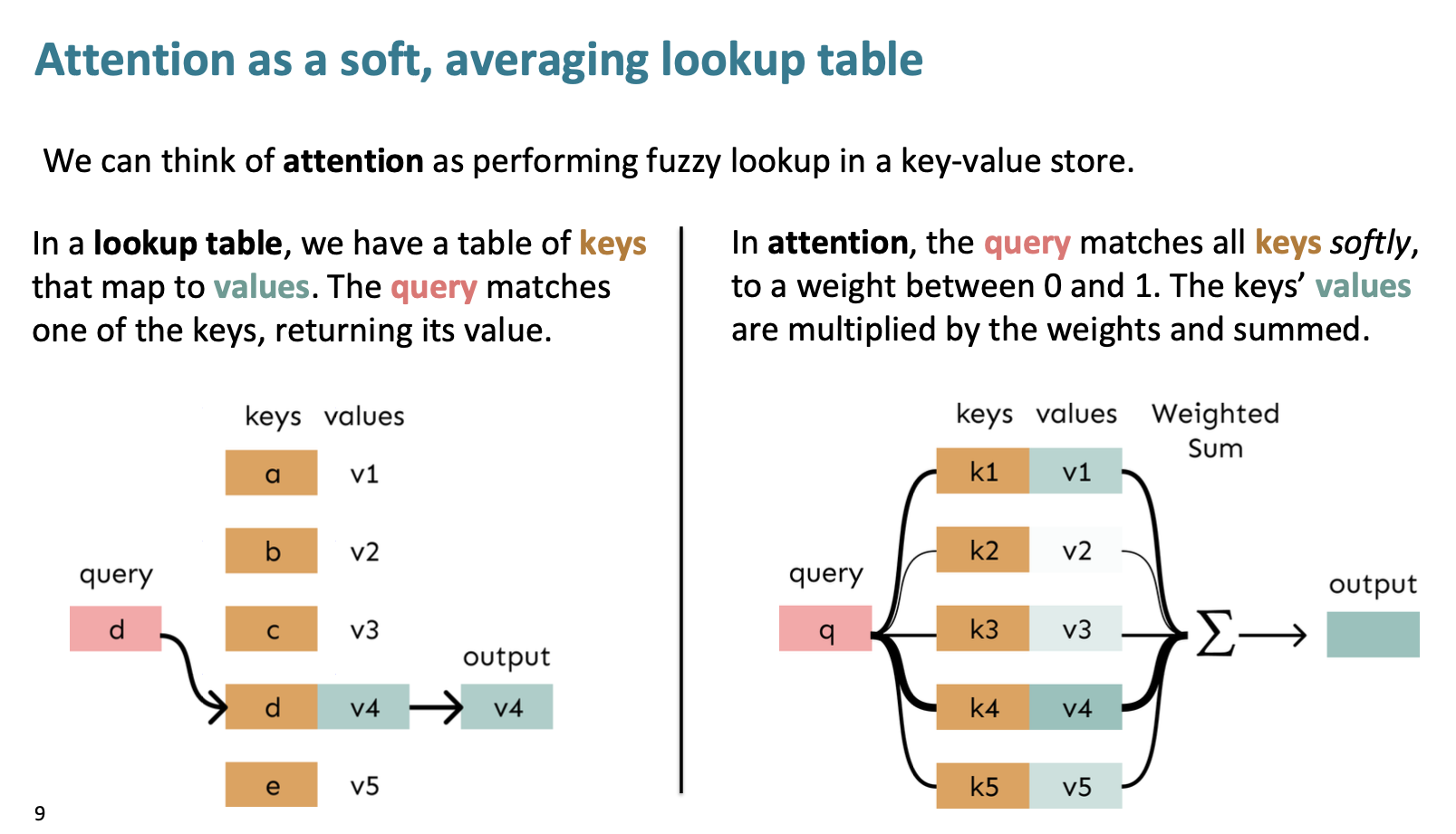
어렵게 생각하지 않아도 된다. lookup table에서 query에 맞는 keys를 선택해서 values 값을 output으로 출력하는 구조와 비슷하다.

Attention은 살짝 다른 것이 모든 keys에 가중치를 두어 접근하고, values를 weighted sum 해서 output으로 출력하는 것이다.

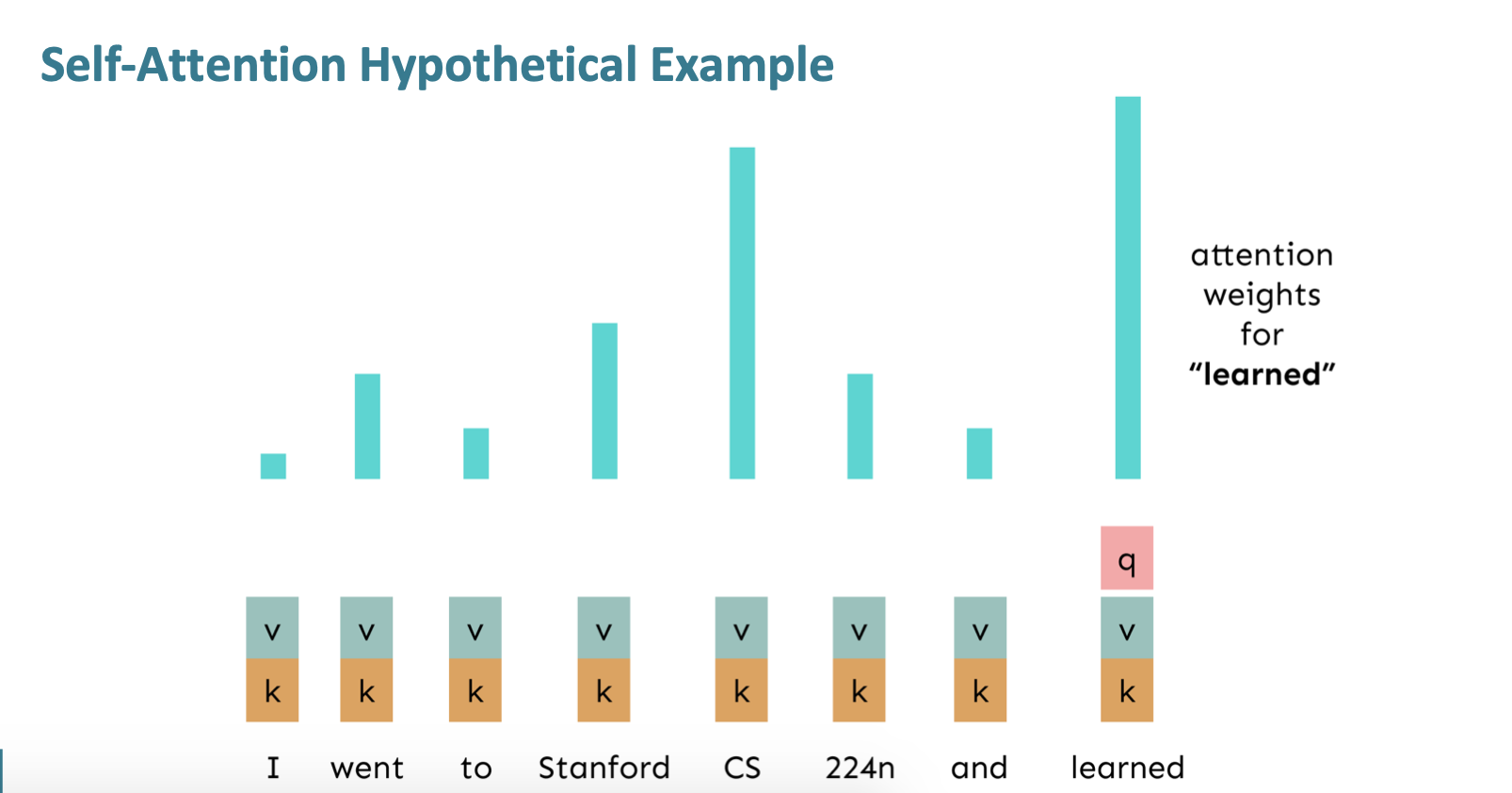
Self-Attention

Self-Attention 이란, 같은 시퀀스에 대해서 keys, queries, values를 추출하는 것이다.

만약 V 사전 안에 $w_{1:n}$를 일련의 단어들이라 하자. 마치

Zuko made his uncle tea.

각각의 단어들은 $w_i$, $x_i = Ew_i$ E는 d x |v| 임베딩 행렬이라 하자.

1. 각각의 가중치 행렬 Q, K, V로 단어 임베딩으로 변환한다. 가중치 행렬의 크기는 dxd 이다.

2. query와 key사이의 비슷함을 계산한다. 그리고 softmax로 정규화한다.
   $e_{ij} = q_i^Tk_j$
   $\alpha_{ij} =exp(e_{ij}) / \sum_{j'} exp(e_{ij'})$

3. output을 계산한다.
   $o_i$ = $\sum_j \alpha_{ij}v_i$

sequence order

self-attention의 장벽 첫번째는 무엇일까?

바로 기존의 문장의 위치를 알 수 없다는 것이다. 순서 정보를 세우지 않으니 우리는 순서 또한 encode할 필요가 있다.

그래서 각각의 sequence index를 벡터로 표현하자.

pi는 position vector이다.

우리는 이전 xi (index i에 대한 임베팅) 벡터와 position vector인 pi를 더한다.

$new xi =xi + pi$

그럼 어떻게 position vector를 구하나?

Sinusoidal position representations

첫번째 방법은
Sinusoidal position representations로 벡터를 구한다.

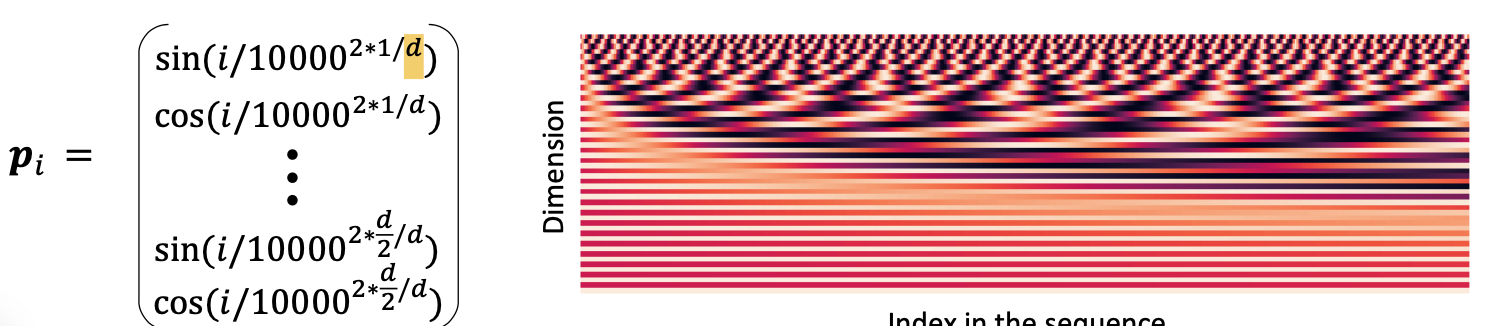
pi는 차원이 깊어질 수록 sin 내부의 주기를 담당하는 값이 커진다.

d가 커지면 $cos(\alpha i)$의 알파값이 커진다. 즉 삼각함수의 주기가 길어지는 것이다. 이를 위 오른쪽 그래프로도 확인할 수 있다.

만약 위 설명이 이해가 되지 않는다면 아래 블로그를 참고하자.

https://skyjwoo.tistory.com/entry/positional-encoding%EC%9D%B4%EB%9E%80-%EB%AC%B4%EC%97%87%EC%9D%B8%EA%B0%80

이러한 방법의 장점은
1. 주기성은 절대적 위치를 나타내지 않아도 된다.
2. 그래서 더 긴 문장에 대해서도 추정이 가능할 수도?
단점은
위의 2번이 진짜로는 실행되지 않는다는 점이다.

대부분의 시스템은 아래의 방법을 사용한다고 한다.

Absolute position representations

그러니까 단어의 '절대적'위치를 학습한다는 것이다.

이 장점은 '유연성' 이다. 각 위치를 데이터에 맞게 학습할 수 있다.
단점은 n을 넘어서는 index는 추정이 불가능하다는 점이다.

두번째 self-attention 단점은 바로

Nonlinearities

self-attention에는 요소별 비선형성이 없다.
레이어를 더 많이 쌓으면 쌓을수록 값 벡터의 평균이 다시 평균이 될 뿐이다.

note의 공식을 보면 여러개의 레이어를 쌓아도 결국 단일 레이어의 모양과 동일해진다.

이를 해결하기 위해서는 feed-forward network를 추가한다.

$m_i = MLP(output_i) = W_2 * ReLU(W_1 output_i + b_1) + b_2$

우선 입력 벡터에 대해서 선형 변환을 취하고 ReLU를 통해 비선형 변환을 해주는 방법이다.

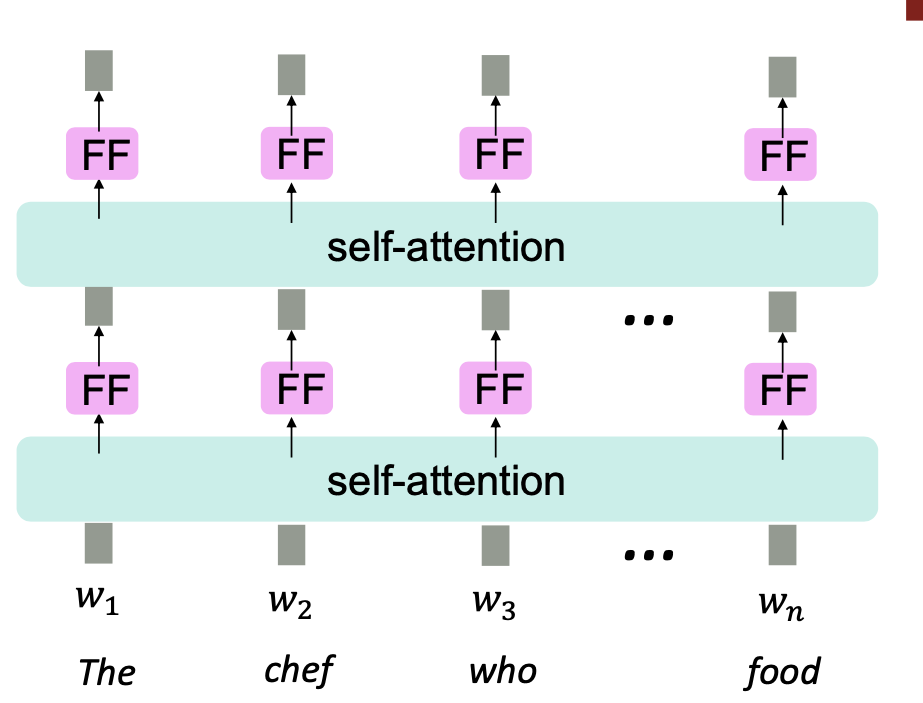
Don't look at the future

만약 self-attention을 decoder에 실행하기 위해서는 우리는 그 다음 단어를 고려하지 않고 실행해야 한다.

따라서 우리는 마스킹 을 통해서 미래의 단어를 제외하고 attention을 진행한다.

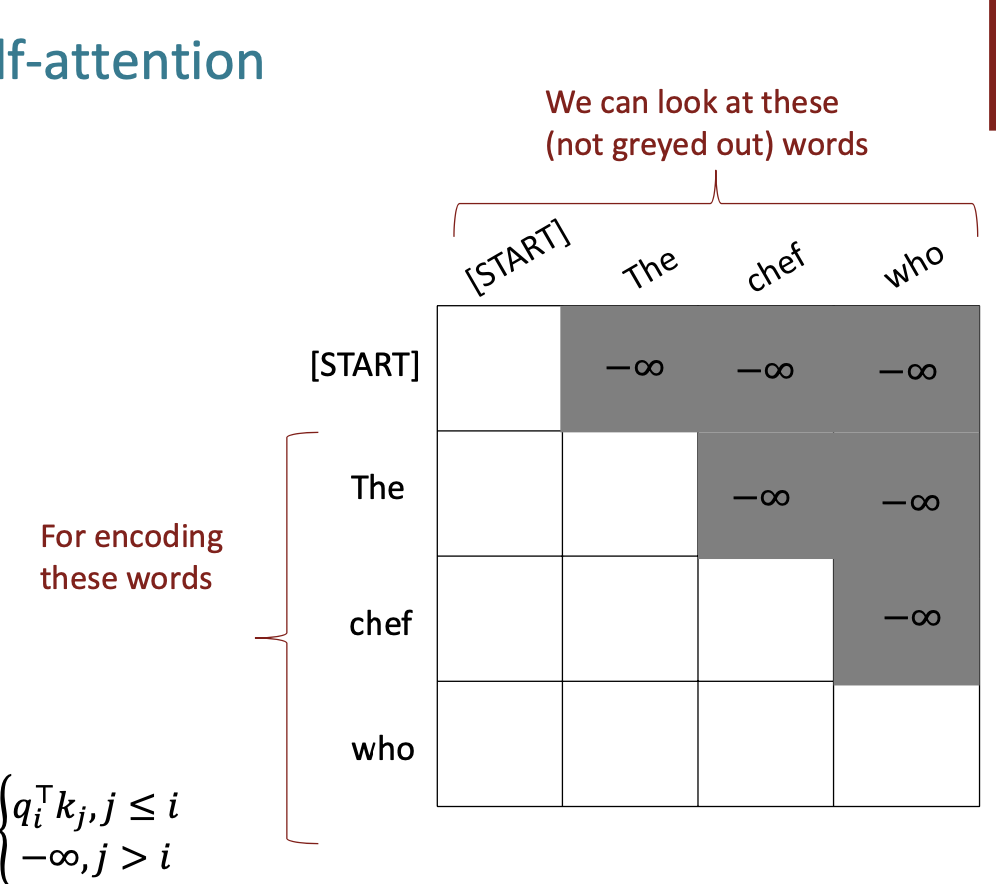
결과적으로 우리는 self-attention에 필요한 것들을 모두 배웠다.

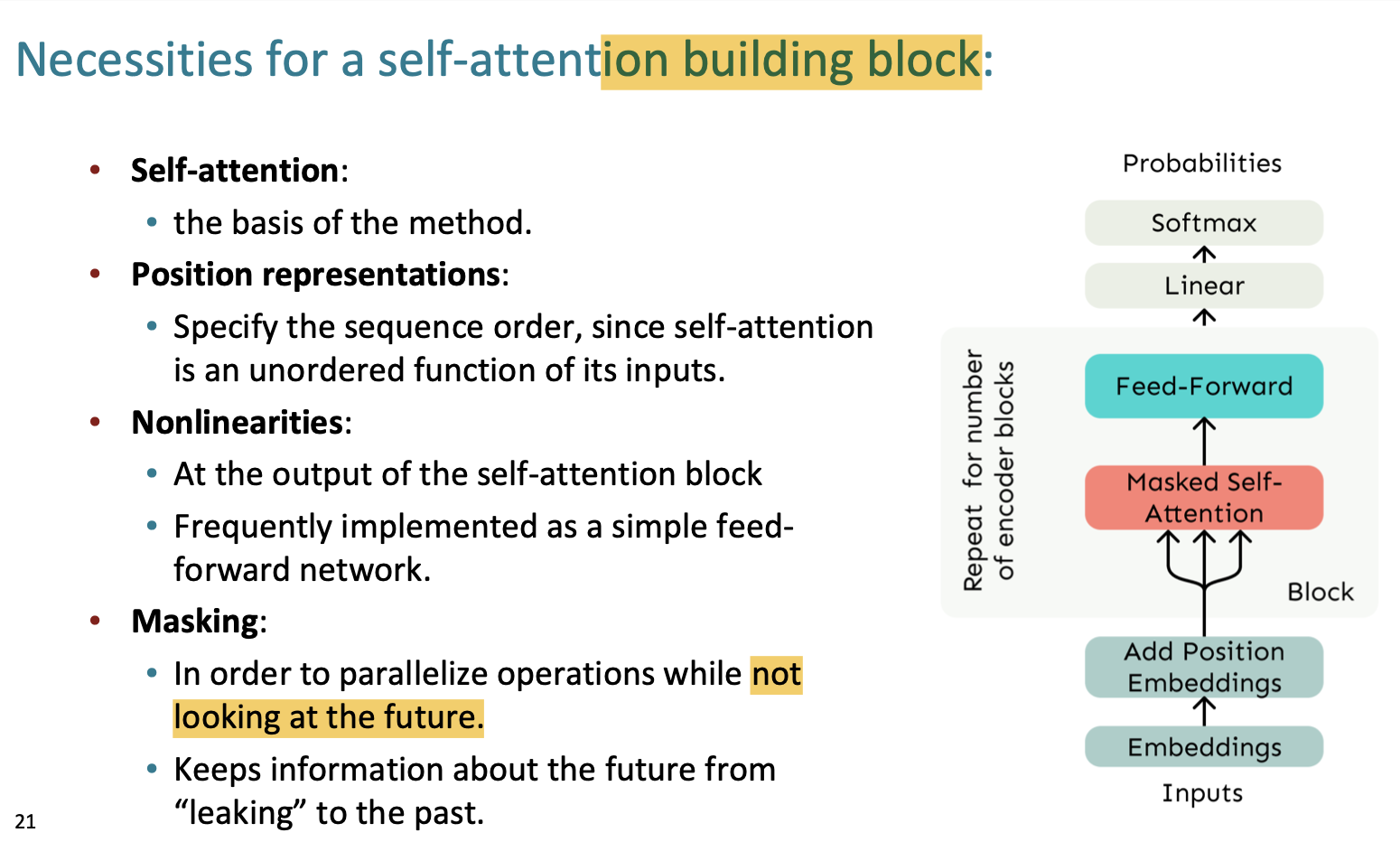
Transformer

자 이제 트랜스포머에 대해 배워보자.

트랜스 포머는 encoder + decoder의 구조를 가지고 있다.

디코더의 구조를 살펴보면,

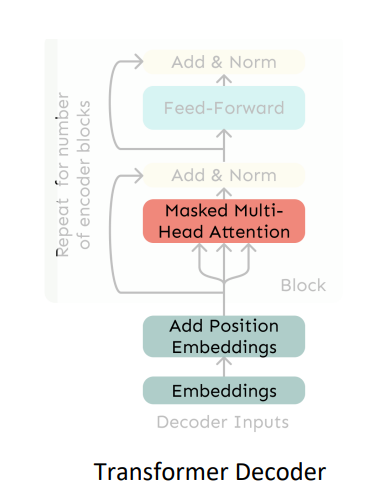
Mutihead Attention 이란 것이 있다.

말 그대로 여러개의 머리를 가지고 있는 attention 이라는 의미인데,,, 뭘까?

사실 attention을 한번 수행한 것과 두번 수행했을 때의 결과가 동일하지 않을 수 있다.

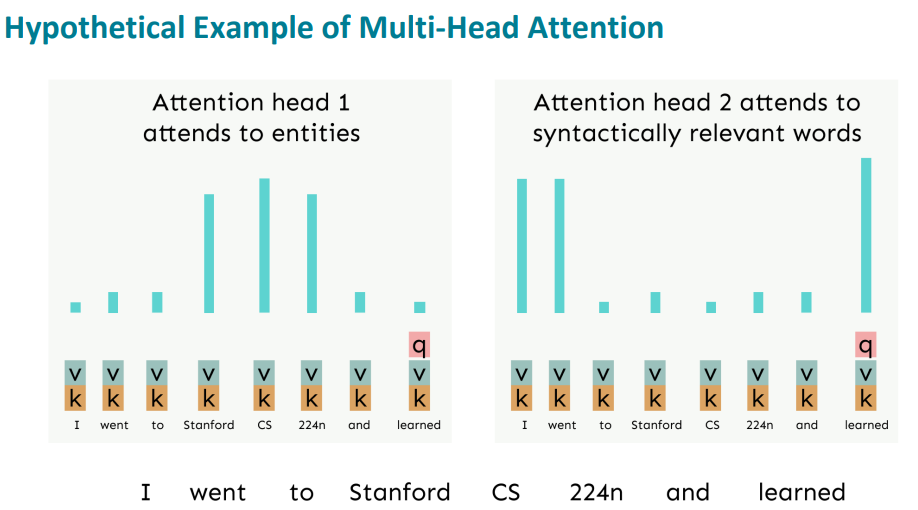
첫번째 Attention의 경우에는 의미론적으로 접근했지만 두번째 Attention의 경우에는 구문론적으로 접근해서 비슷한 단어를 가리킨 것을 확인할 수 있다.

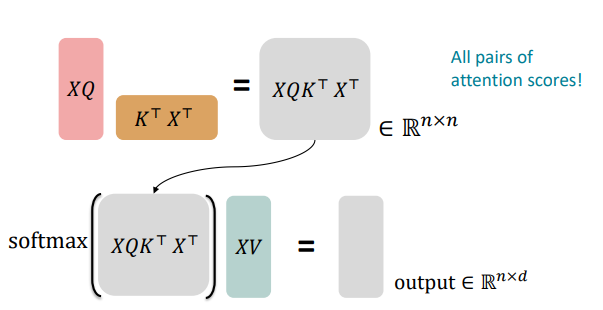
만약 X가 nxd 크기의 입력 벡터를 concatenation 한 것이라 하자. key, query, value를 각각 K, Q, V 라고 하자.

우리는 XK, XQ, XV 를 먼저 구한다. 각각의 크기는 n x d 이다.
그리고 output은 softmax(𝑋𝑄(𝑋𝐾)⊤)𝑋V 이다.

Multi-head attention

h는 attention head의 개수이다.

h의 개수만큼 우리는 attention을 독립적으로 수행할 것이다.

$output_l = softmax(XQ_lK_l^TX^T) x XV_l$ output의 크기는 d/h이다.

그리고 output은 모든 heads를 결합한다.

output = [$output_1; ... output_h$]Y, Y는 dxd 크기이다.

각 head는 각자 다른 것을 중요시하게 생각해서 보고 value vector를 다르게 구성한다.

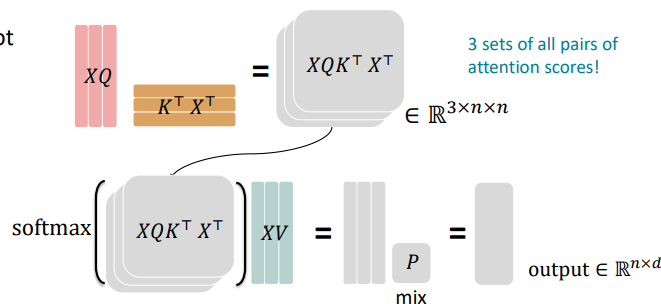
이전 그림과 다른 것은 바로 input을 3개로 나누었다는 것이다. 그래서 총 3개의 attention score 행렬을 가지게 되었다. 3개의 행렬은 모두 같은 size 이다.

Scaled Dot Product

Scaled Dot Product는 attention 보조기구이다.
d의 숫자가 커질 수록 내적 또한 커지게 된다. 그래서 softmax 안에 넣는 입력값이 커지고 이는 기울기를 작게 만든다고 한다...(??)

그래서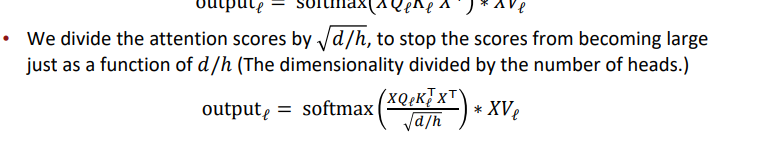

$\sqrt{d/h}$로 나누어준다.

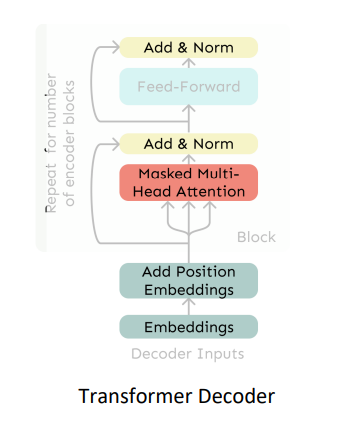
다시 트랜스포머 구조를 살펴보자.

우리는 일단 muti-head self-attention을 수행했다.

그리고 나서 우리는 최적화 방법을 수행할 것이다.

바로

• Residual Connections
• Layer Normalization
  이라는 것이다.
  이를 우리는 "Add & Norm" 이라 한다.

Residual connections

Residual connections ,, 뭔가 연결을 하는 것 같다.

맞다. 우리는 이전의 값 -> layer -> 결과값
이렇게 보통 계산하게 된다.

이를 $X^i = Layer(X^{i-1})$ 이라 하자.

우리는 이 방법에서 살짝 뭔가를 추가한다.

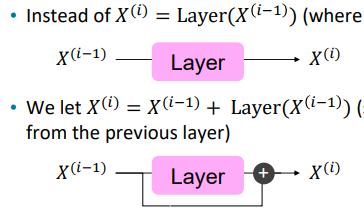
$X^i = X^{i-1} + Layer(X^{i-1})$ 즉 결과값에 이전의 입력값을 추가하는 것이다.

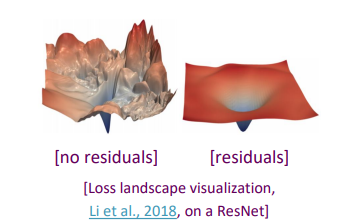
residual 을 한 것과 안한 것의 차이가 분명하다.

Layer normalization

두번째 방법이다.

train을 좀 더 faster 하게 한다.

각 레이어에서 unit 평균과 표준 편차로 정규화(normalize) 하여 히든 벡터 값에 정보가 없는 변동(variation)을 줄이는 것이다

각 독립적인 벡터에 평균을 빼고 표준편차로 나눠준다. 이때 엡실론을 아주 작은 숫자로 두어서 exploding을 방지한다.

결과적으로 우리는

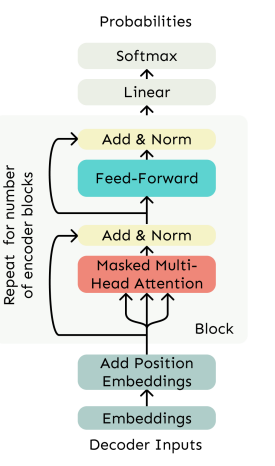
여러 Block으로 구성된 decoder를 만들었다.

이제 Encoder를 보자.

사실 Econder는 Decoder와 거의 유사하다. 하지만 다른 점은 Masking을 할 필요가 없다는 검이다.
우리는 bidirectional context를 원한다. 왜냐하면 source 문장은 처음부터 끝까지 우리가 아는 문장이기 때문이다.

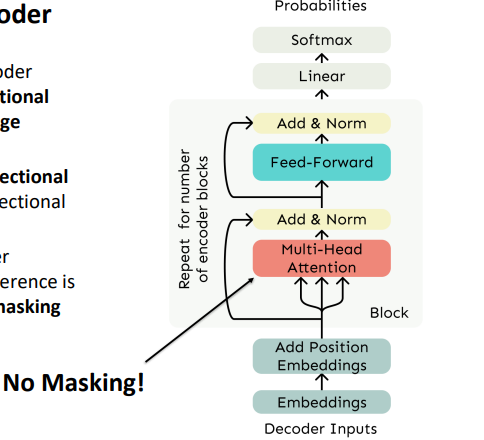
따라서 거의 Decoder와 유사한 형태를 가진다.

Encoder - Decoder

그럼 인코더 - 디코더의 구조를 살펴보자.

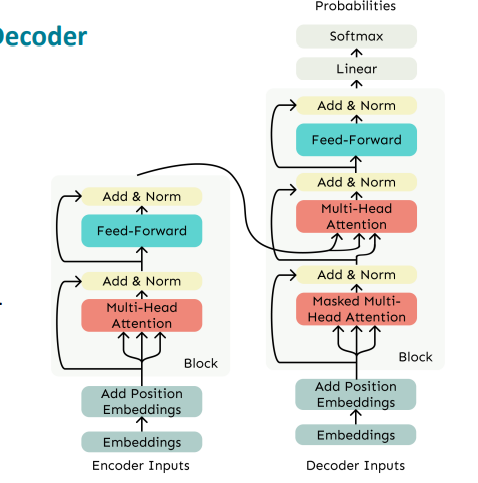
기계 번역에서 우리는 source 문장에 대해서는 bidirectional 한 구조를 원하고 target에 대해서는 unidirectional 구조를 원한다.
이때 우리는 normal한 Transformer 를 사용한다.

우리의 Transformer Decoder에 cross-attention을 추가한다. 이는 encoder의 output을 활용해서 decoder의 attention을 수행하는 것이다.

Cross attention

h1, h2, ..., hn이 encoder의 output이라 하자.
z1, z2, ..., zn이 decoder의 input vector라고 하자.

우리는 $k_i = Kh_i, v_i = Vh_i$라 하고, (k는 keys, v는 value)
$q_i = Qz_i$ 라 한다. (Q는 쿼리)

즉 encoder의 output + decoder의 input 을 attention 하는 것이다.

Great results with Transformers

Transformer가 등장하면서 perplexity가 급감했다.

여러 Transformer가 업데이트 되면서 perplexity는 점점 감소했다.

Drawbacks and variants of Transformers

그럼에도 여전히 단점은 존재한다고 한다.

1. Quadratic compute in self-attention
   self-attention 계산을 하기 때문에 모든 단어 쌍에 대해서 유사도를 계산해야 한다. 따라서 계산량이 많다.
2. 메모리 사용량이 많다. 각 단어간의 관계를 나타내는 가중치를 저장해야한다.
3. Position representations
   절대적 위치를 저장하는 것만이 유일한 방법일까?
   relative linear position attention, Dependency syntax-based position도 있다.
4. 시퀀스 길이 제한
   시퀀스 길이가 n 이고 n이 계속 커진다면 총 계산해야 하는 양은 O(n^2d)로 굉장히 많아진다.
   만약 d(차원) 이 1000 정도라고 가정하자. 하나의 문장은 n <= 30 일 때, n^2 <= 900 이된다.
   만약 n이 엄청나게 큰 숫자가 들어간다면 처리하는 데 많은 어려움이 있을 것이다.

즉 시퀀스 길이가 늘어남 -> 비용 증가
비용 감소 -> 정확도 감소, 정상작동 x

이러한 문제를 해결하기 위해 많은 노력들을 해왔지만, 여전히 Transformer라는 점은 중요하다.

---

앞으로 Transformer 보다 더 좋은 모델이 나올 수 있을지 궁금하고, 머리 좋은 천재들은 많으니까 가능할지도 모르겠다는 생각을 하면서 블로그 정리를 마친다.