Chapter 9

K-Means clustering

k-평균 집단화는 비지도 학습 알고리즘이다.
이 알고리즘의 목적은 주어진 데이터를 k개의 클러스터로 나누는 것이다. 데이터 내의 패턴을 찾아 유사한 특성을 가진 데이터 포인트 끼리 묶어 그룹화를 진행한다.

기본 원리

1. 클러스터 수 선택 : 몇개의 클러스터로 나눌지 결정. k선택
2. 중심점 초기화 : k개의 클러스터에 대한 초기 중심점을 무작위로 선택 또는 특정 방법으로 선택
3. 할당 : 데이터 포인트($x_n$)들을 가장 가까운 중심점에 할당.
4. 업데이트 단계 : 클러스터의 중심점($\mu_k$)을 새롭게 계산. 각 클러스터내의 모든 데이터 포인트의 평균위치로 중심점을 이동
5. 반복: 할당과 업데이트 반복해서 클러스터가 변화가 없거나 특정 기준에 도달할 때까지 반복

$J = \sum_{n=1}^N \sum_{k=1}^K r_{nk}||x_n - \mu_k||^2$

이 함수는 각 데이터 포인트들의 할당된 벡터 $\mu_k$로부터의 거리들을 제곱해서 합한 것.

$x_n$이 집단 k에 할당되면 $r_{nk} = 1$이고 j=k가 아닌 j에서는 0이다.

우리의 목표는 J를 최소화하는 $r_{nk}$와 $\mu_k$를 찾는 것이다.
=> n번째 데이터 포인트를 집단 중심들 중 가장 가까운 것에 할당한다는 의미이다.

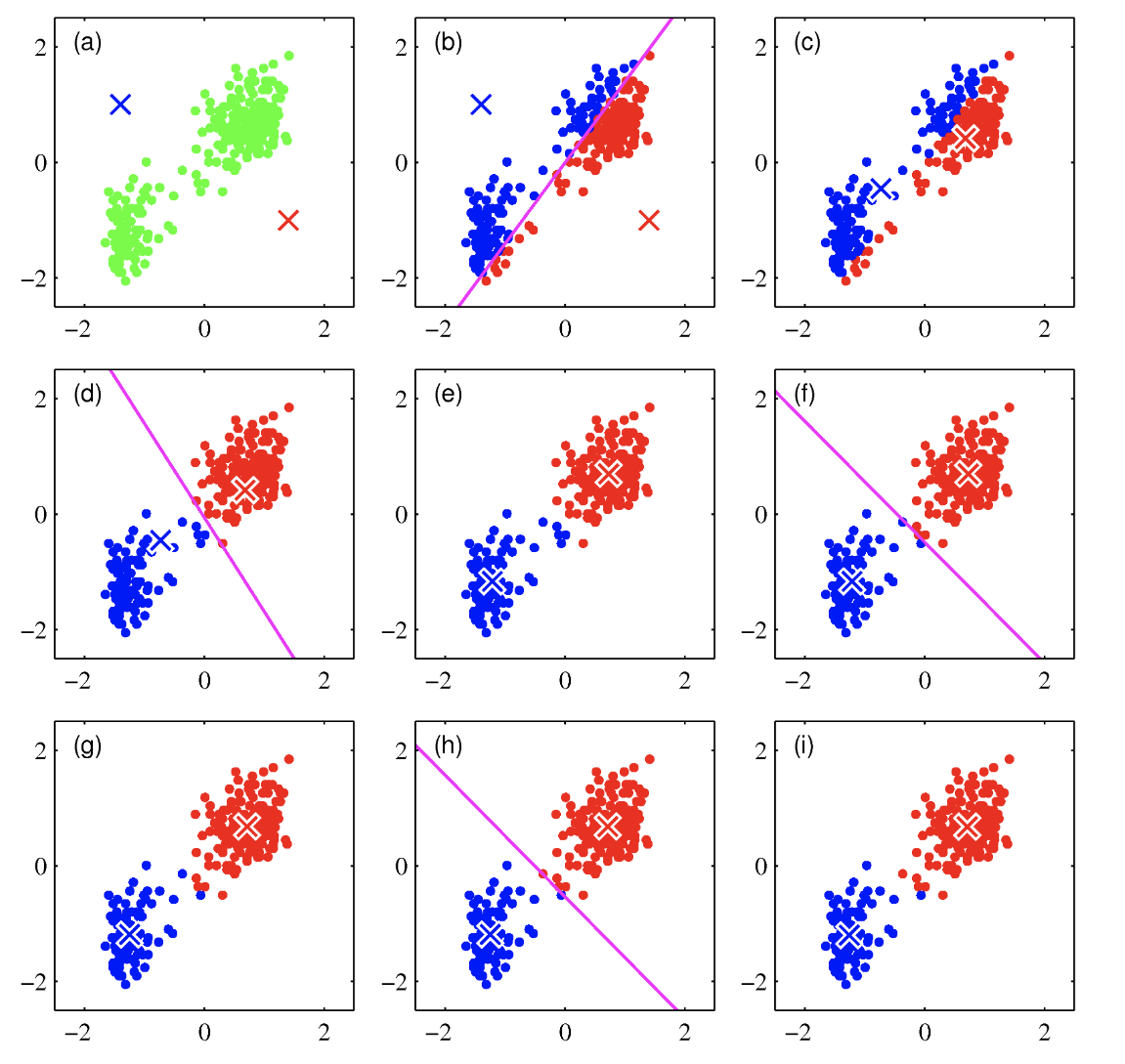
a부터 순서대로 보면, 우선 초기 중심값을 고의적으로 별로 좋지 못하게 설정해서 수렴하기까지 몇단계가 걸리도록 했다. k=2일때의 모습이고, (b)에서는 어떤 중심에 더 가까운지에 따라 빨간색 아니면 파란색으로 표시된 것을 볼 수 있다. 또한 두 중심집단을 나누는 선인 자주색 선을 확인할 수 있다. (c)에서는 각각의 집단 중심은 해당 집단의 평균값으로 다시 계산된다.

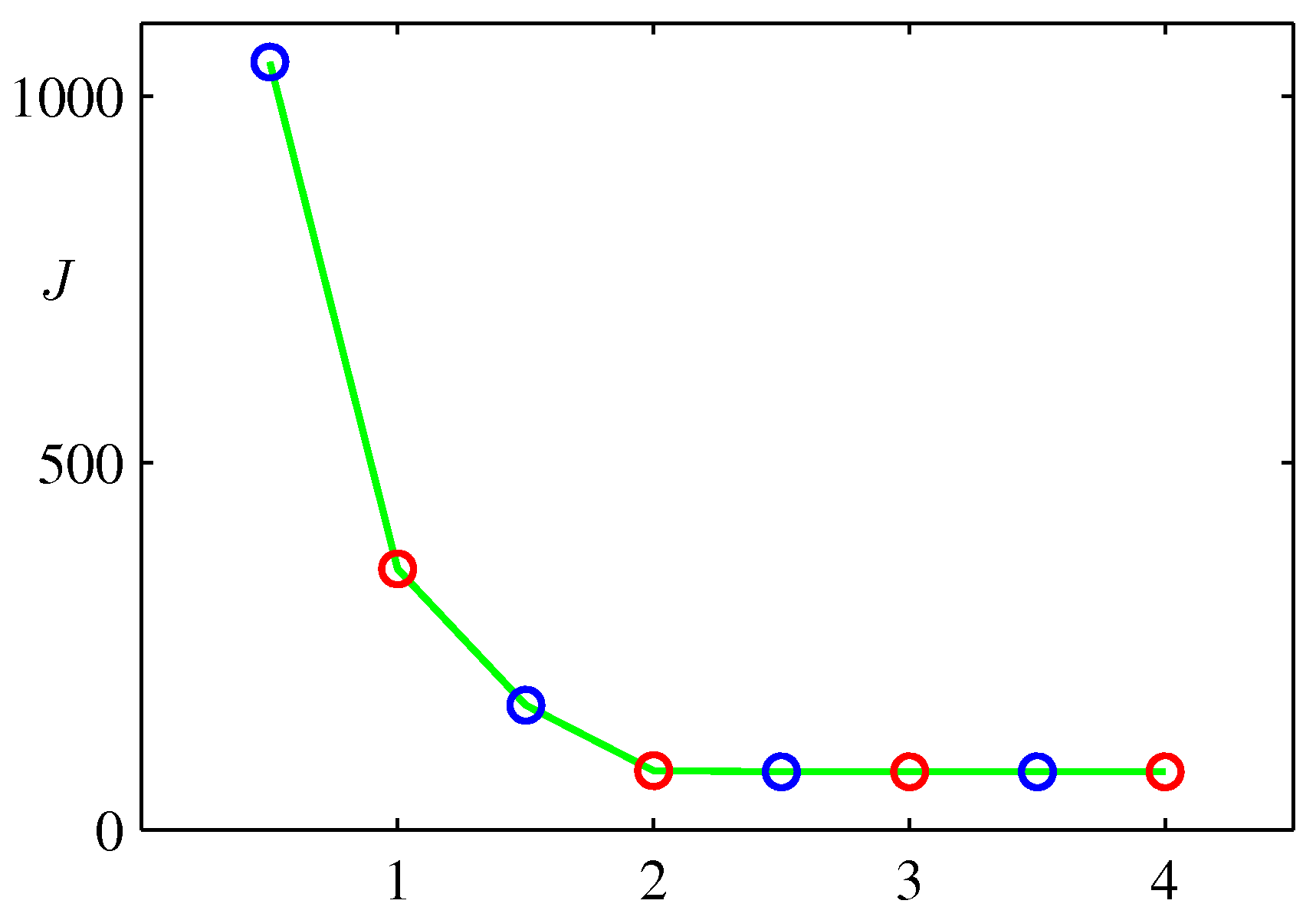
위 그림은 EM과정을 반복할 때마다 J값이 줄어드는 것을 나타내는 그림이다.

한계

K 집단 알고리즘의 한계는

• 데이터 포인트들을 가장 가까운 집단에 명확하게 할당하는 것이 적절한 일인지 불분명할 수 있다.
• 이상값에 대해 강건하지 않다.
• k값을 사용자가 선택해야한다.

이미지 분할과 압축

K-Means 알고리즘을 적용해서 이미지 압축을 해보자

이 알고리즘은 원 이미지를 k개의 색채만을 이용해 다시 그리는 것과 같다. 여기서는 단지 K-means가 이미지 분할에서 어떤식으로 작동하는 지만 보여주기 위해 예시로 사용했다. 이 방법이 좋고 뛰어난 방법이라는 것은 아니라는 것이다.

K-means를 통해 데이터를 압축하는 것도 가능하다.

데이터 압축에는 무손실 데이터 압축과 손실 데이터 압축이 있는데, 집단화 알고리즘을 이용해 손실 데이터 압축을 실행할 수 있다.

• K-means 를 시행한 다음 N개의 포인트 각각에 대해서 그 데이터 포인트가 할당된 집단 k가 무엇이었는지, 각 집단 k의 중심값 $\mu_k$도 저장한다.

• 원래보다 훨씬 더 적은 데이터만을 필요로 한다.

가우시안 혼합 분포

가우시안 혼합 분포에 대한 EM 알고리즘

• 식
  $\mu_k = 1/N_k \sum_{n=1}^N \gamma(z_{nk})x_n$
  $\sum_k = 1/N_k \sum_{n=1}^N \gamma(z_{nk})(x_n - \mu_k)(x_n-\mu_k)^T$
  $\pi_k = N_k/N$

모델 학습 단계

1. 초기화 : 초기 평균, 공분산, 혼합계수를 설정
2. 기대값 E단계: 각 데이터 포인트가 각 가우시안 분포에 속할 확률 계산.
3. 최대화 M단계: 평균, 공분산, 혼합계수를 위 공식을 이용해 구함
4. 반복: E, M단계를 반복해 파라미터가 수렴할 때까지 반복

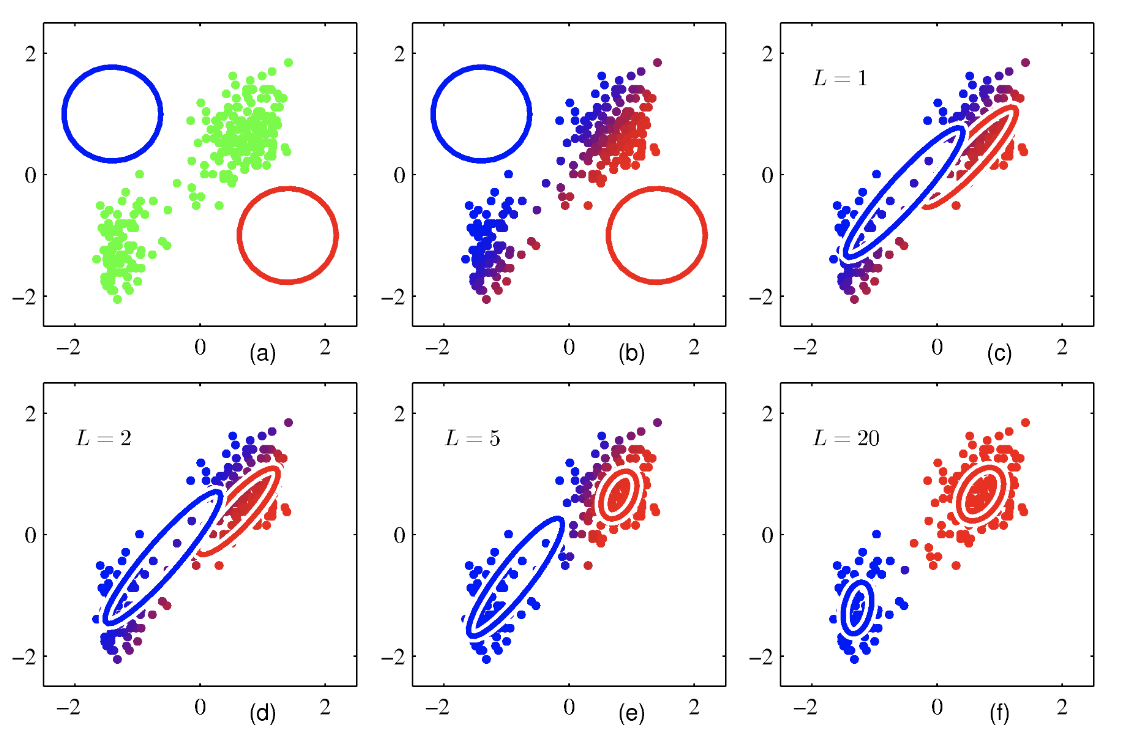
(a)에는 데이터 포인트들이 녹색으로 그려져있다. 혼합 모델의 초긱값을 바탕으로 두 가우시안 성분의 단위 표준 편차 경로가 각각 파란색, 빨간색 원으로 표시되고 있다.

(b)에는 최초 E단계 결과를 보이고 있다. 각 데이터 포인트들은 파란색 성분과 빨간색 성분의 사후 분포 비율에 따라 파란색과 빨간색을 섞어 칠한다. 두 집단에 속할 확률이 반반이라면 보라색을 띈다.

(c) 최초 M단계 결과이다. 파란 가우시안 분포의 평균값이 데이터 집합의 전체 평균쪽으로 이동했다. 파란색 잉크들의 무게 중심으로 이동한 것이다. 파란색 가우시안 분포의 공분산은 파란색 잉크들의 공분산과 동일하게 설정 되었다. 빨간색도 마찬가지이다.

d,e,f는 2,5,20 단계의 EM사이클이 반복된 결과이다. f에서는 거의 수렴한 것을 확인할 수 있다.

베이지안 선형 회귀에 대한 EM

베이지안 선형 회귀에 대한 EM알고리즘에 대해 알아보자.

이전에 우리는 증거를 계산하고 그 결과식의 미분값을 0으로 설정해서 초 매개변수 $\alpha$ 와 $\beta$에 대한 재 추정식을 구했는데, EM알고리즘을 통해서 $\alpha$ 와 $\beta$ 값을 구하는 방법을 알아보자.

참고로 베이지안 선형 회귀에서 $\alpha$ 와 $\beta$는 모델의 초 매개변수로서, 모델의 성능과 학습 과정에 중요한 역할을 한다.

$\alpha$ : 이 매개변수는 가중치 벡터의 선행 분포에 대한 역분산 또는 정밀도를 나타낸다. $\alpha$ 는 다시 말해서, 가중치 크기에 대한 제약을 의미한다. 모델의 복잡도를 의미한다.
$\alpha$ 값이 커지면 제약이 강해져서 모델이 단순해지고
$\alpha$ 값이 작아지면 제약이 줄어들어 모델이 복잡해진다.

$\beta$ : 이 매개변수는 관측된 데이터의 노이즈 또는 오차의 역분산을 의미한다. $\beta$는 데이터 잡음에 대한 모델의 내성을 의미한다.
$\beta$ 값이 커지면 모델의 민감도가 낮아지고(잡음을 덜 고려)
$\beta$ 값이 작아지면 모델의 민감도가 커진다.(잡음을 많이 고려)

EM 알고리즘을 사용해서 초 매개변수 $\alpha$ 와 $\beta$를 재추정 해보자.

초 매개변수 $\alpha$ 와 $\beta$를 재추정

• E단계

1. 잠재 변수의 기대값 추정: 현재 초 매개변수 $\alpha$ 와 $\beta$를 사용해서 이 가중치들의 기대값을 추정한다. 가중치에 대한 사후 분포를 계산하고 이 분포의 평균 또는 mod를 잠재 변수의 기대값으로 사용한다.

• M단계

1. 초 매개변수 재추정: E단계에서 계산한 기대값을 사용해서 $\alpha$ 와 $\beta$를 재추정한다.
   $α_{new} =가중치 개수 / ∑가중치 기대값^2$
   $β_{new} =관측치 개수 / ∑잔차^2$

수렴할 때 까지 EM과정을 반복하면 된다.

일반적 EM 알고리즘

하나의 확률적 모델을 가정하자. 이 모델의 모든 관측 변수들은 X, 모든 은닉 변수들은 Z로 지칭하자. 결합 분포 p(X,Z| $\theta$)는 $\theta$ 로 지칭되는 매개변수 집합에 의해 조절된다. 우리의 목표는 다음처럼 주어지는 가능도 함수를 최대화 하는 것이다.
$p(X,Z| \theta) = \sum_Z p(X,Z|\theta)$

$p(X,Z| \theta)$는 관측 변수와 은닉 변수가 주어진 매개변수에 대한 모델의 결합 확률 분포이다.

• 주변 가능도 함수 $p(X|\theta)$ : 은닉 변수 Z를 모두 합산하여 얻는 관측 데이터 X에 대한 주변 가능도 함수이다. 즉 $p(Z|\theta) = \sum_Z p(X,Z|\theta)$

• 이 주변 가능도 함수를 직접 최대화하는 것은 계산상 어렵다. 따라서 변분 추론(Variational inference)를 사용한다. -> 복잡한 확률 분포를 더 간단한 분포로 근사하는 방법이다.

로그 가능도 분해

완전 데이터 가능도 함수 $p(X,Z|\theta)$ 에 대한 최적화는 훨씬 쉽다고 가정하자. 그 다음 잠재 변수들에 대한 분포 q(Z)를 도입할 것이다.

로그 가능도 $ln p(X|\theta)$는 두 부분으로 분해될 수 있다.

$ln p(X| \theta) = L(q,\theta) + KL(q||p)$ 로 분해가 가능하다고 한다.

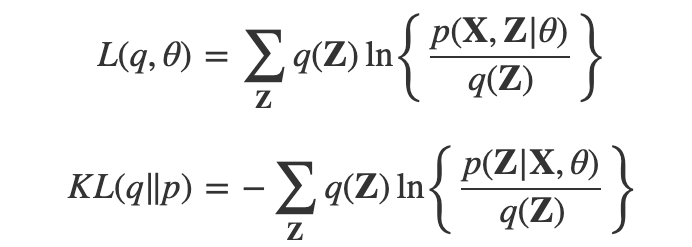
1. $L(q,\theta)$: 변분 하한(Evidence Lower Bound) 또는 로그 가능도 하한이다.
2. KL(q||p): 이는 q(Z)와 실제 은닉 변수 분포 p(Z|X,$\theta$)간의 쿨백-라이블러 발산이다. 두 분포간의 '거리'를 측정한다.

• 변분 추론의 목표 : L을 최대화함으로써 로그 가능도의 하한을 최대한 높이는 것이다. 동시에 KL을 최소화해서 q(Z)를 실제 은닉분포에 가깝게 만드는 것이다.

EM 알고리즘

• E단계: 이 단계에서 주어진 매개변수 $\theta$에 대해 q(Z)를 $p(Z|X,\theta)$에 근사하도록 설정. KL을 최소화하는 것과 동일하고 L을 최대화하는 것임.
• M단계: L을 최대화하는 새로운 $\theta$를 찾음. 로그 가능도의 하한을 높이는 것과 같음.

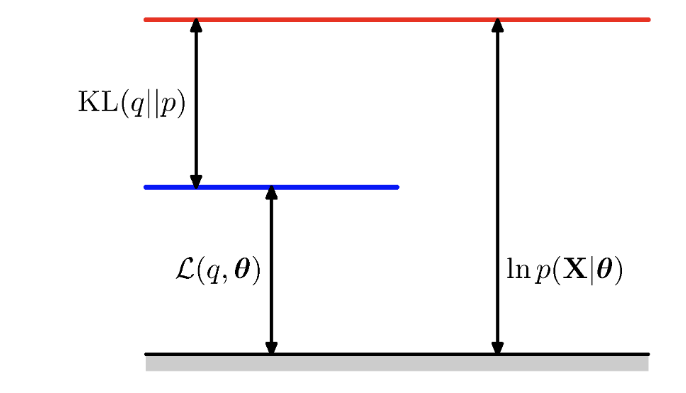
맨 처음 아무것도 진행하지 않은 상태이다.

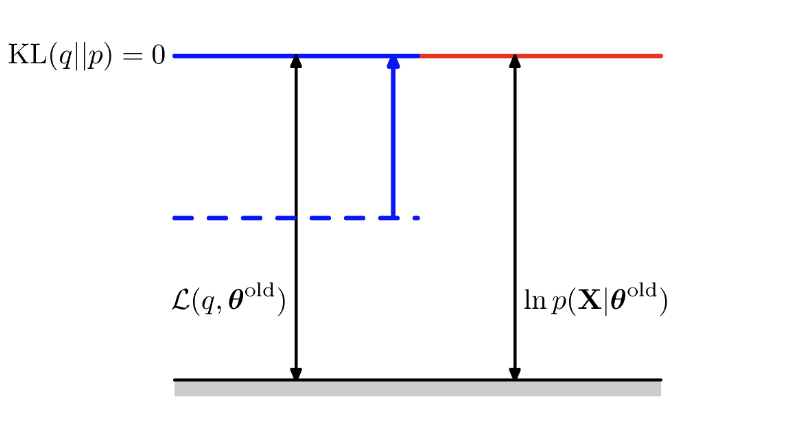
E-step을 진행한 다음의 상태이다. KL을 최소화해서 0을 만들고 L을 최대화한다.

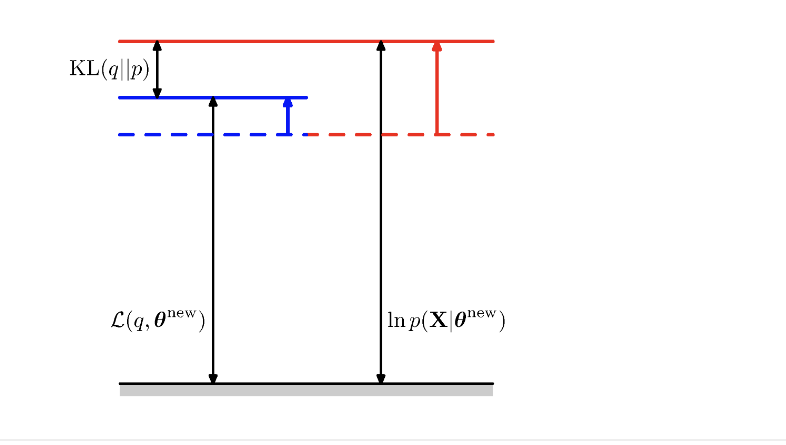
M-step 즉 수정된 새로운 $\theta_{new}$를 찾고 난 다음의 결과이다. L함수를 최대화하는 파라미터를 구하면 전체 로그 가능도 함수의 최대값이 증가하고 마찬가지로 L함수의 값도 증가할 수 있다.