[백준] 1788번. 피보나치 수의 확장

[백준] 1788번. 피보나치 수의 확장

또보나치

1. 문제

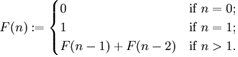
수학에서, 피보나치 수는 위의 점화식과 같이 귀납적으로 정의되는 수열이다. 위의 식에서도 알 수 있듯이, 피보나치 수 F(n)은 0 이상의 n에 대해서만 정의된다.

하지만 피보나치 수 F(n)을 n이 음수인 경우로도 확장시킬 수 있다. 위의 식에서 n>1인 경우에만 성립하는 F(n)=F(n-1)+F(n-2)를 n<=1일 때도 성립되도록 정의하는 것이다. 예를 들어 n=1일 때 F(1)=F(0)+F(-1)이 성립되어야 하므로, F(-1)은 1이 되어야 한다.

n이 주어졌을 때, 피보나치 수 F(n)을 구하는 프로그램을 작성하시오. n은 음수로 주어질 수도 있다.

2. 입력

첫째 줄에 n이 주어진다. n은 절댓값이 1,000,000을 넘지 않는 정수이다.

3. 출력

첫째 줄에 F(n)이 양수이면 1, 0이면 0, 음수이면 -1을 출력한다. 둘째 줄에는 F(n)의 절댓값을 출력한다. 이 수가 충분히 커질 수 있으므로, 절댓값을 1,000,000,000으로 나눈 나머지를 출력한다.

4. 풀이

• n이 양수일 때와 음수일 때 점화식을 다르게 했다.
• 어차피 양수, 음수 번갈아 쓰진 않아서 배열은 하나만 했다.
• 양수일 때, arr[n] = arr[n-1] + arr[n-2]
• 음수일 때, arr[n] = arr[n-2] - arr[n-1]
하기 전에 n을 양수로 바꿔준다.

5. 처음 코드와 달라진 점

• long long으로 시작했는데 10억으로 나머지 연산을 해서 두 개 더해줘도 21억을 안 넘어서 int로 바꾸었다.
• 문제를 제대로 안 읽어서 바로 피보나치 결과값만 출력했다.
• 처음엔 나머지 연산도 안 했다.
• 0일 때도 따로 분리하는 걸 안 했다.
• 나중에 보니까 양수일 때는 10억으로 나머지 연산하는데 음수일 때는 1억으로 하고 있더라
  복붙했는데 중간에 0이 하나 지워졌나 보다

6. 코드

#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;
int arr[1000001];

int negative_fibo(int num) {
	arr[0] = 0;
	arr[1] = 1;
	for (int i = 2; i <= num; i++){
		arr[i] = (arr[i - 2] - arr[i - 1]) % 1000000000;
	}
	return arr[num];
}

int positive_fibo(int num) {
	arr[0] = 0;
	arr[1] = 1;
	for (int i = 2; i <= num; i++) {
		arr[i] = (arr[i - 1] + arr[i - 2]) % 1000000000;
	}
	return arr[num];
}

int main() {
	cin.tie(NULL);
	ios_base::sync_with_stdio(false);

	int n;
	cin >> n;
	int answer = n >= 0 ? positive_fibo(n) : negative_fibo(-n);
	
	if (answer < 0) cout << "-1\n";
	else if (answer == 0) cout << "0\n";
	else cout << "1\n";
	cout << abs(answer);
}