
ML lec 04 - multi-variable linear regression (new)
Recap

Predictingexam score : regression using one input (x)
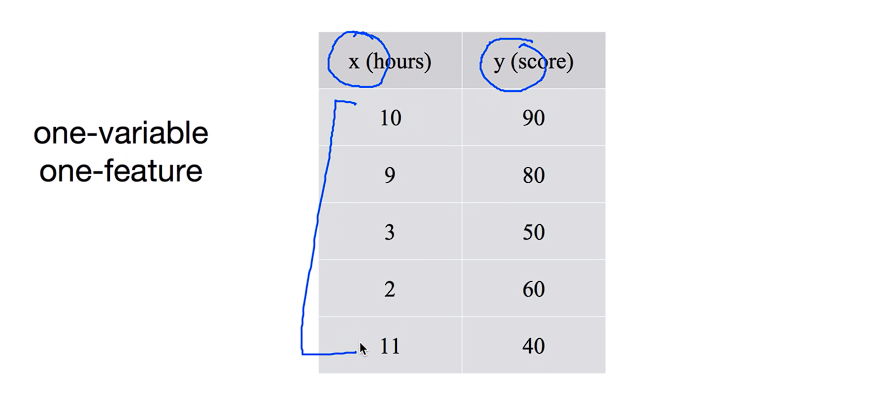
one-variable 일 경우에는 이전과 같은 방법으로 계산하면 된다.
Predictingexam score : regression using three inputs (x1, x2, x3)
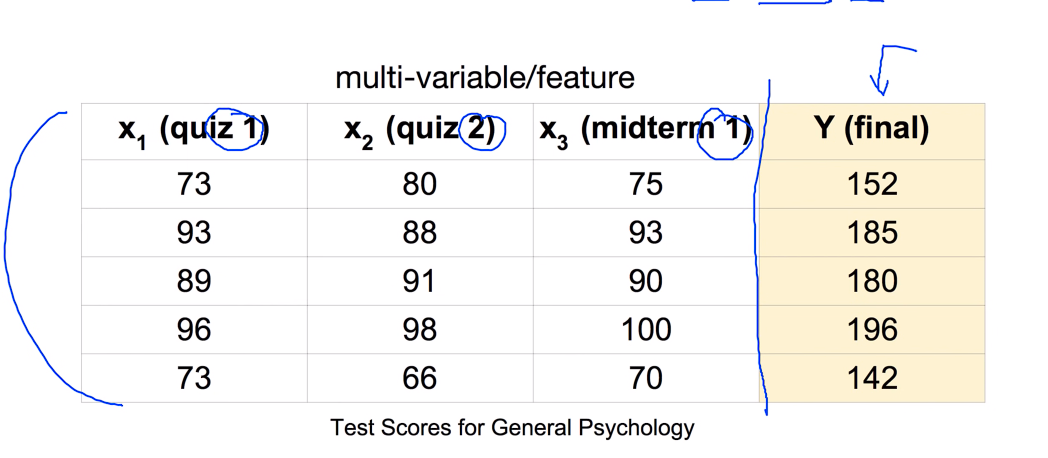
여러개의 variable일 경우에는 이전과 똑같은 방법으로는 계산을 할 수 없다.
Hypothesis
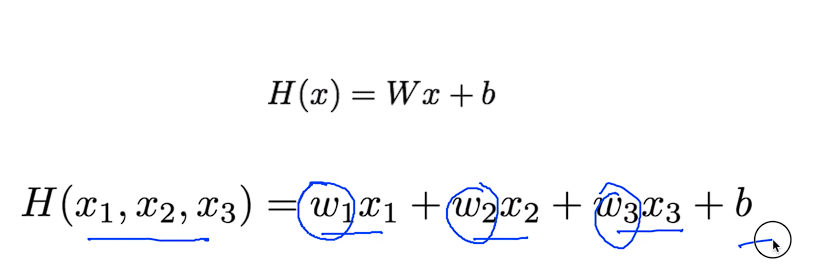
Hypothesis에 대한 식은 위와 같은데 x의 값이 3개면 아래의 식 처럼 만든다.
Cost function
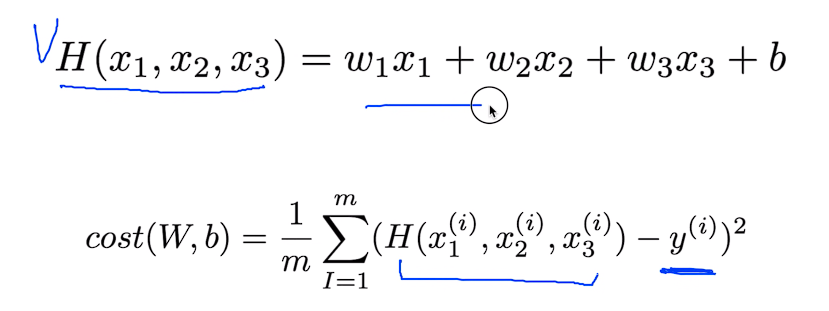
Cost function도 마찬가지로 이전의 Cost Function이랑 같지만 H(x) 값만 H(x1, x2, x3)로 바뀌었다.
Multi-variable
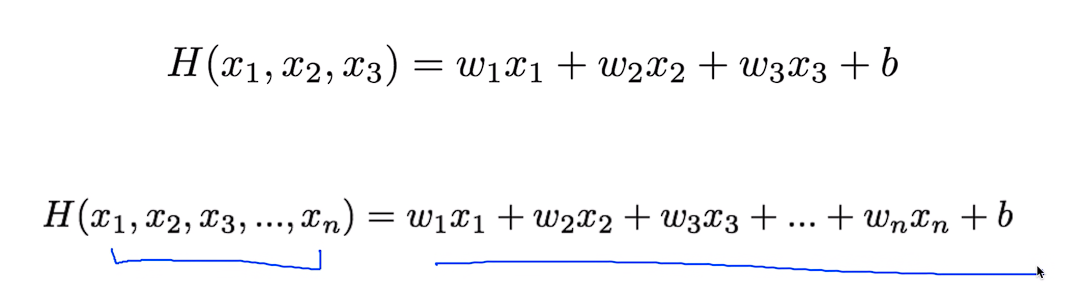
더 많을 경우도 마찬가지로 100개 200개 일때도 쭉 늘려주면 된다. 그런데 이렇게 하다보면 사용하기 불편할거같은데 좀 잘 처리하는 방법이 없을까?
Matrix
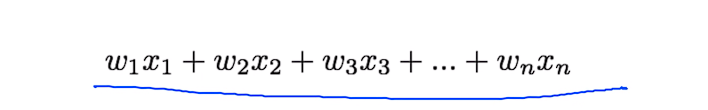
x의 값이 단순히 여러개면 계속 식을 이어가면 되지만 그 x의 값이 무수히 많다면?
Matrix multiplication
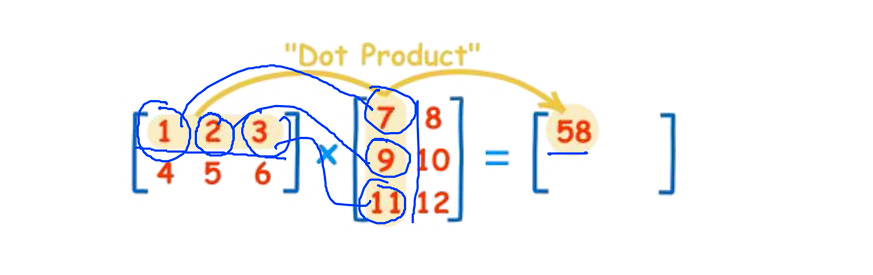
Matrix(행렬) 을 사용 하면 된다. 매트릭스의 곱은 그림처럼 계산하면 된다.
Hypothesis using matrix
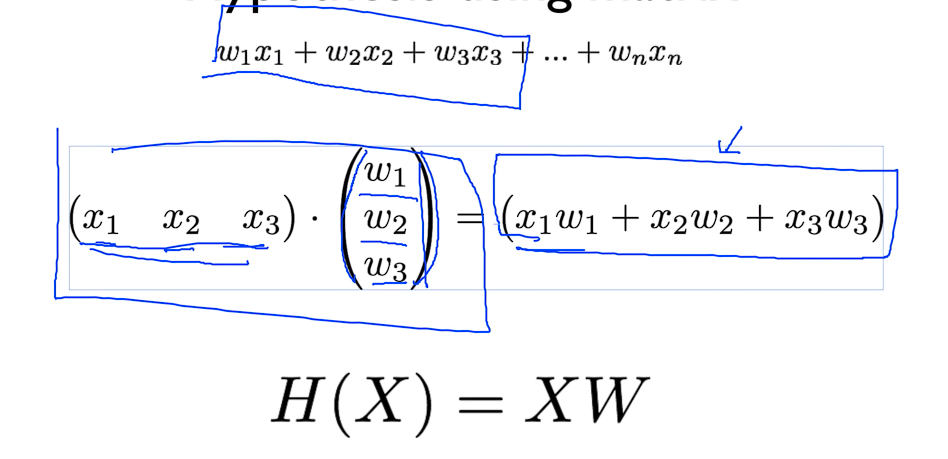
매트릭스를 쓸 때는 X를 앞에다 쓰는데 어차피 곱하는 식이라 순서는 상관이 없다 bias는 간단히 하기 위해서 잠시 생략을 했다
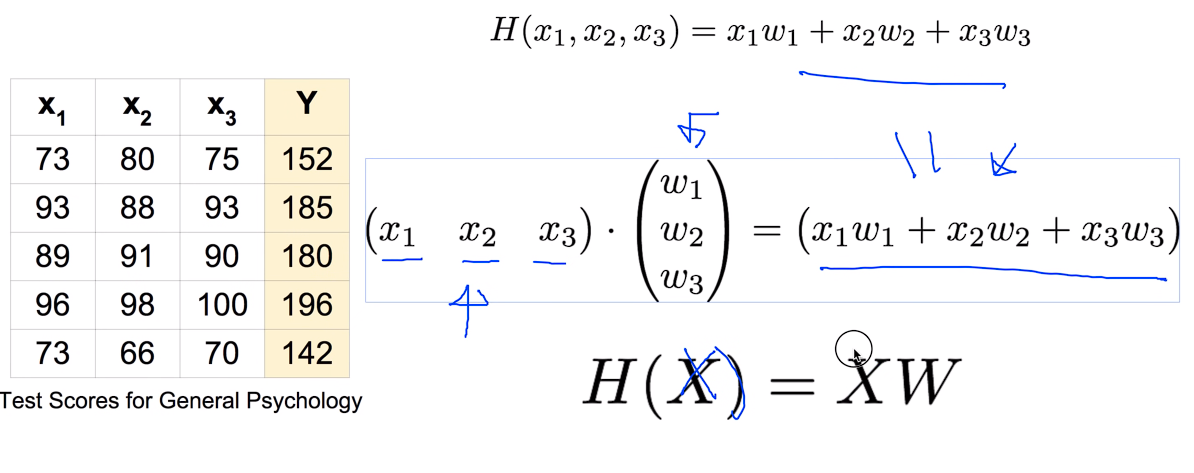
우리가 Hypothesis를 matrix를 이용한 폼으로 나타낸다면 H(X) = XW 이다.
Many x instances
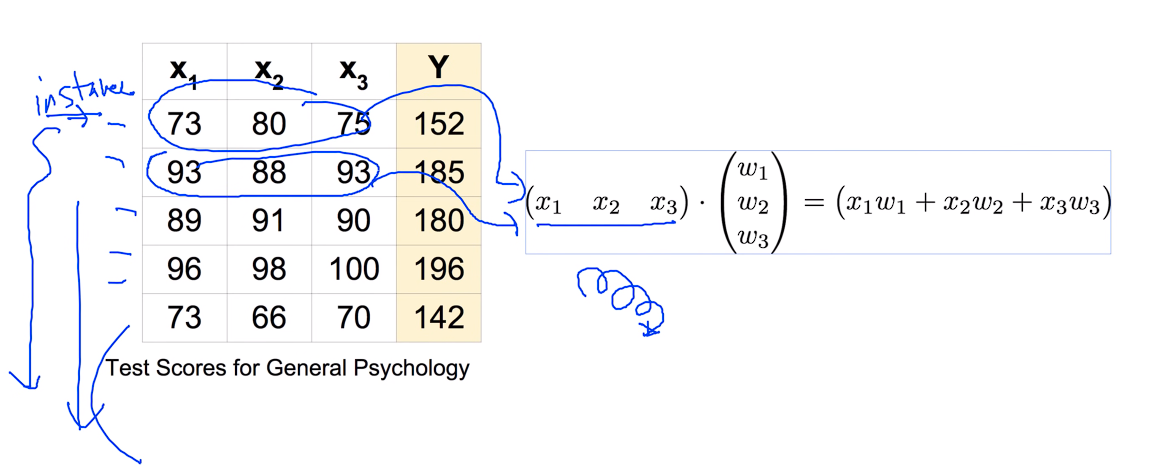
Hypothesis using matrix

매트릭스에 놀라운 장점은 인스턴스가 많을 때 각각의 인스턴스를 계산할 필요없이 전체를 긴 매트릭스에 넣고 그냥 W를 곱해버리면 원하는 값이 나온다
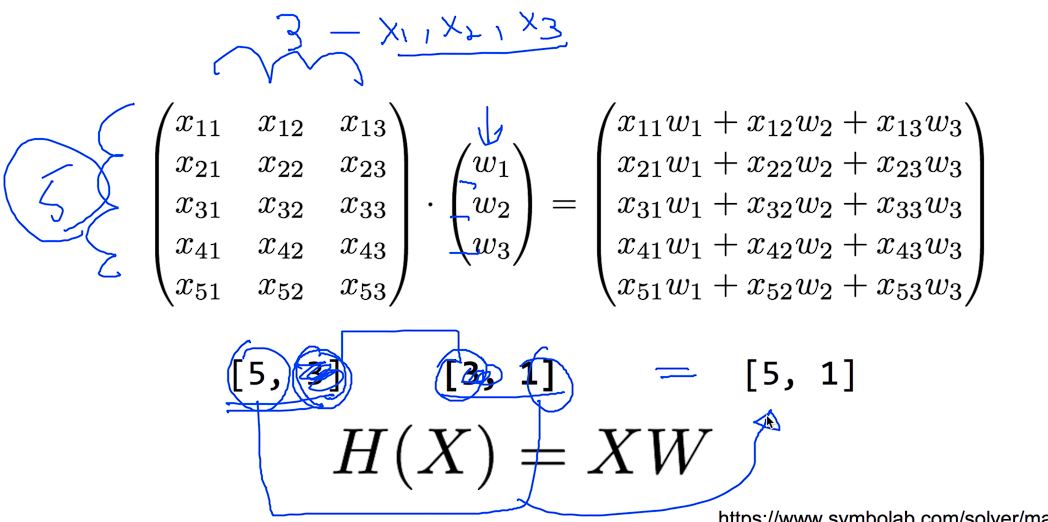
[5, 3] 같은 경우 5는 인스턴스의 갯수 3은 x1, x2, x3 같이 x의 variable 갯수
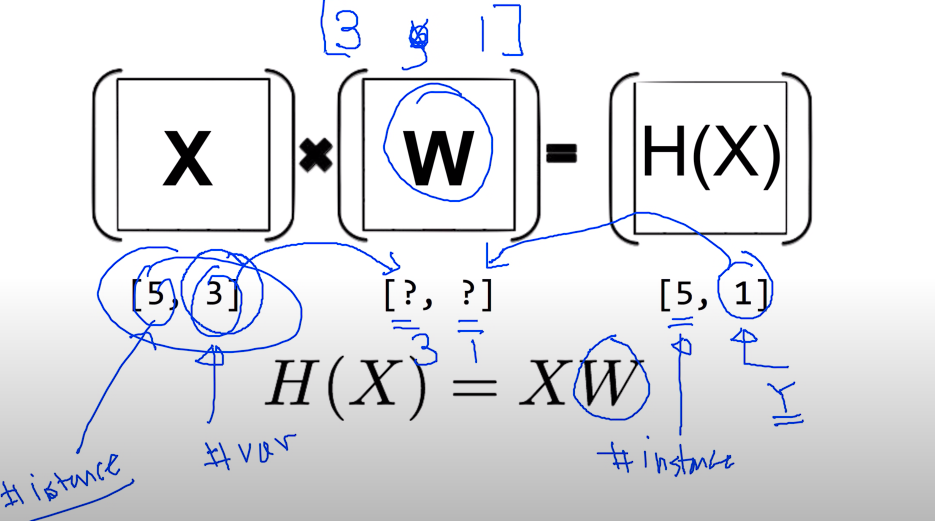
W의 크기를 구하는 방법은 X의 variable 갯수를 W의 인스턴스의 갯수로 H(X)의 variable 갯수를 W의 variable의 갯수로 대입하면 된다.
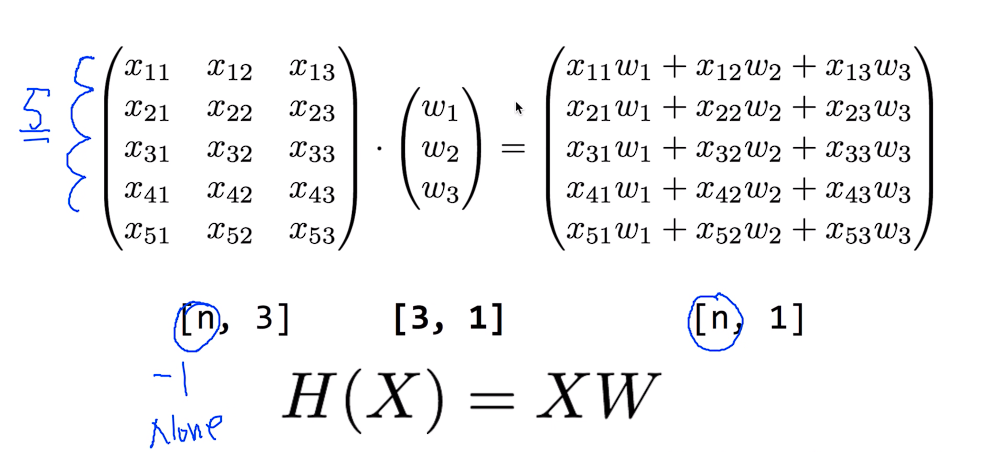
텐서플로우에서는 n을 None로 표현한다
Hypothesis using matrix (n output)
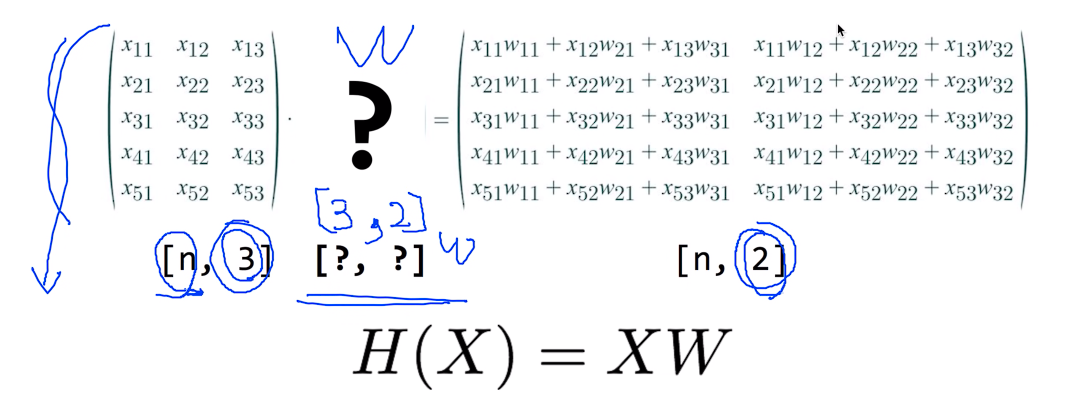
매트릭스를 사용하면 멀티 베리어블에 경우에도 쉽게 처리할 수 있고 인스턴스가 많을 경우에도 n으로 쉽게 처리할 수 있고 출력이 하나가 아니라 여러개 일 경우에도 쉽게 처리할 수 있는 장점이 있다
WX vs XW
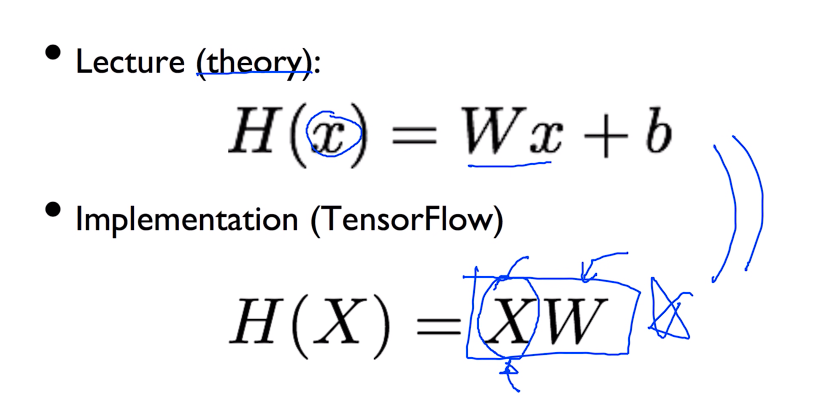
총 정리 : 실제로 x가 하나로 주어지지 않고 다수로 주어지는 경우가 많아 실제로 구현할 땐 H(X) = XW 로 많이 구현하고 위의 식과 아래의 식은 같다고 보면 된다.
ML lab 04-1: multi-variable linear regression을 TensorFlow에서 구현하기(new)
Hypothesis using matrix

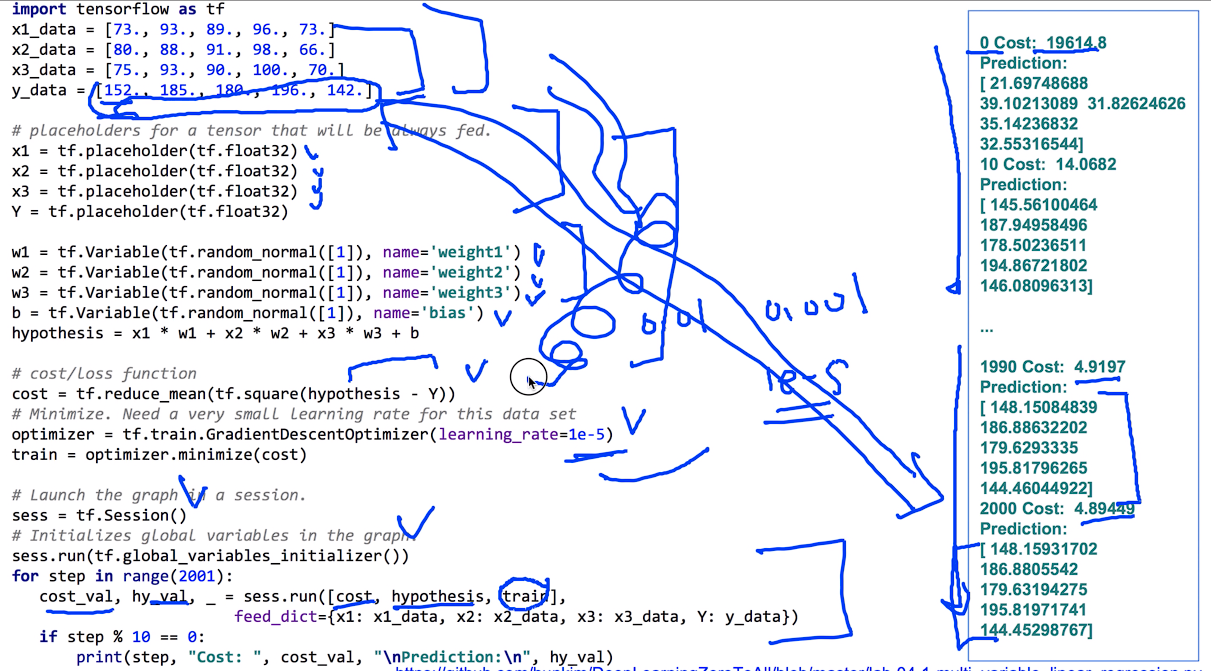
위의 코드는 잘 사용하지 않는 예
Matrix

텐서플로우에서는 n개를 None로 표시한다
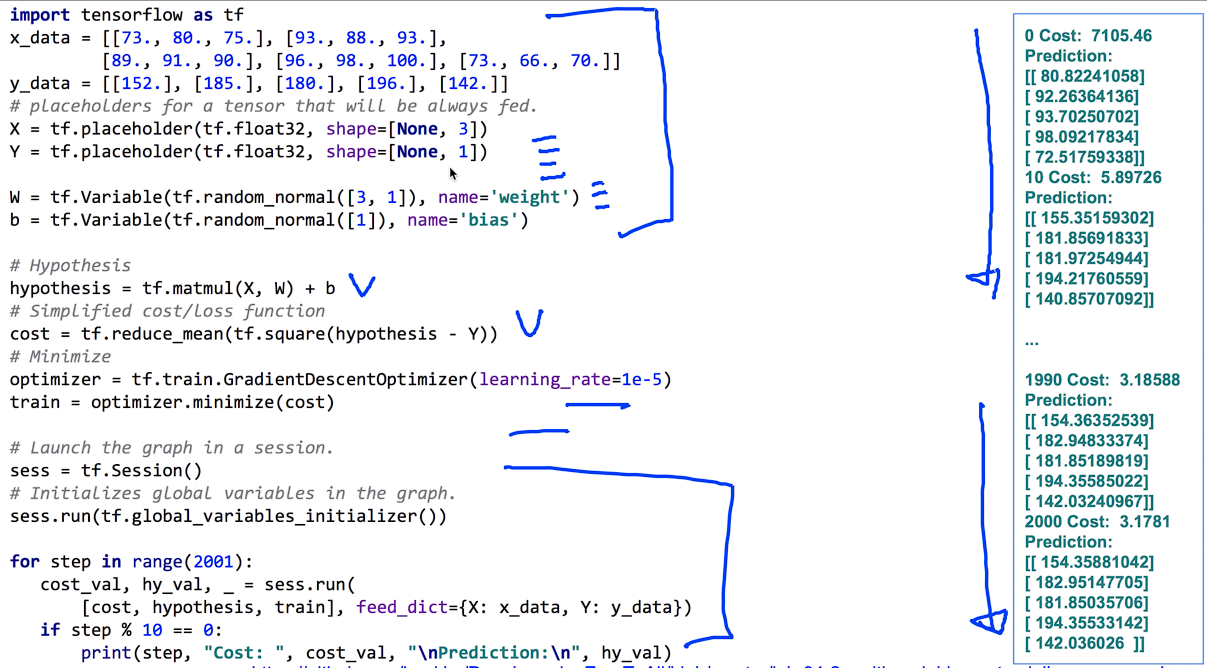
Matrix를 활용한 코드는 더 간단하면서도 variable의 갯수가 대량일 때도 쉽게 구현할 수 있다.
ML lab 04-2: TensorFlow로 파일에서 데이터 읽어오기 (new)
Loading data from file
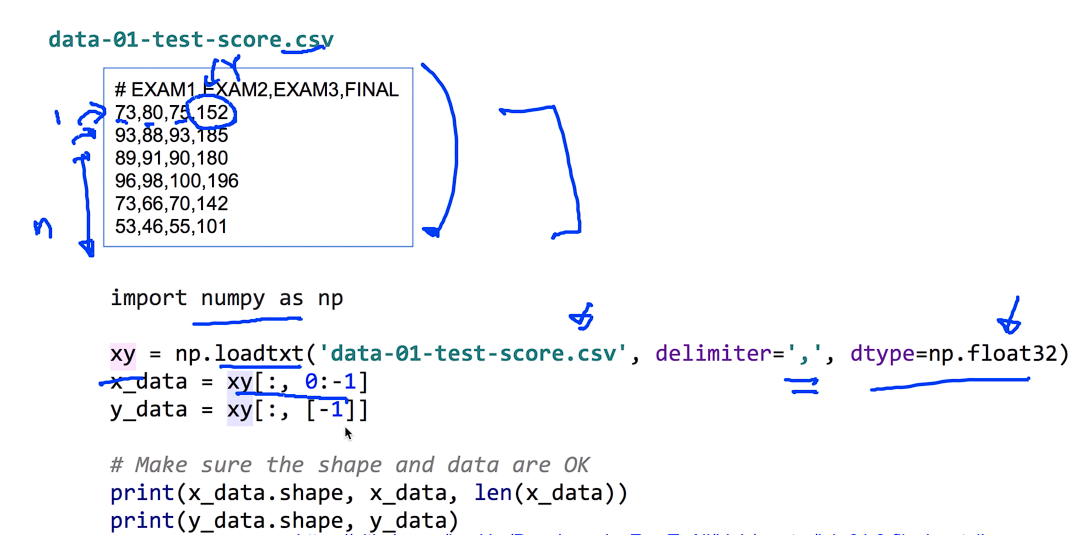
,(콤마)로 나뉘어진 파일 ==> .csv 파일
Slicing

파이썬 리스트의 강력한 기능중 하나인 Slicing
Indexing, Slicing, Iterating

Loading data from file
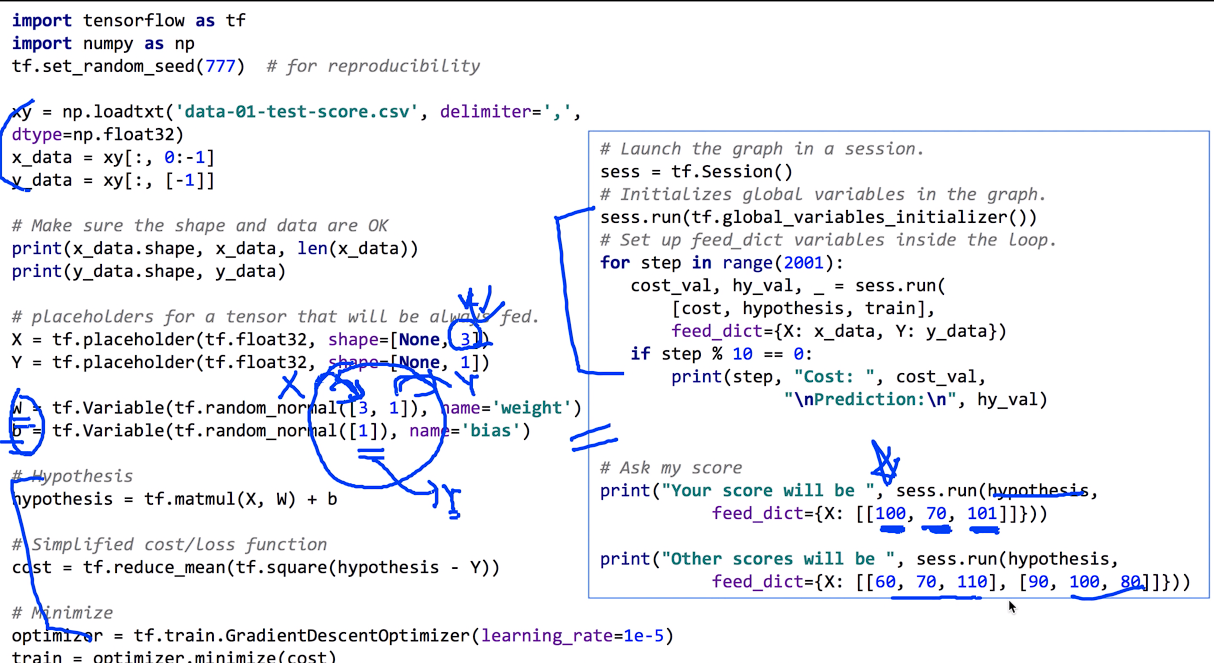
Output
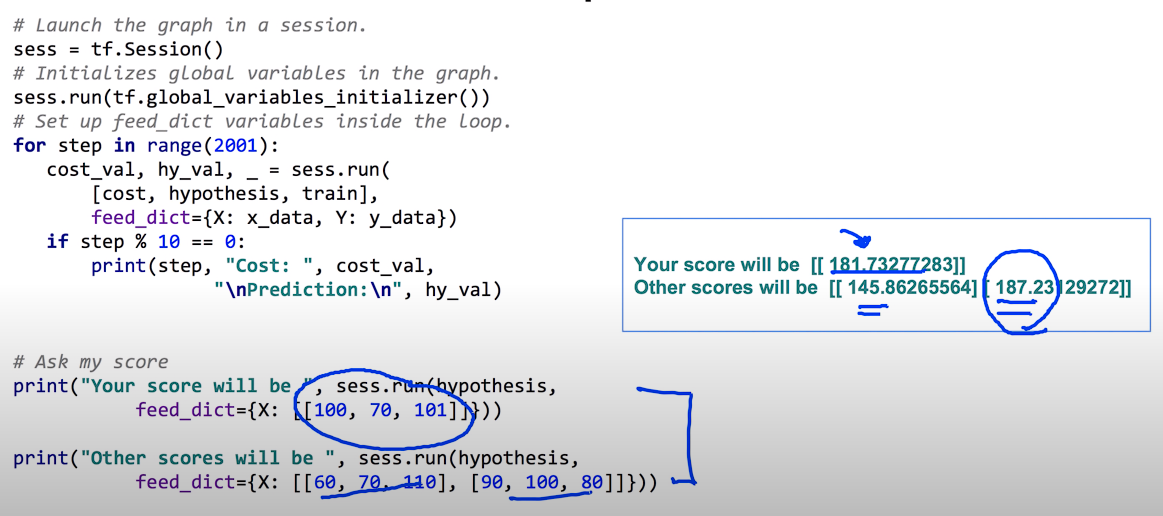
이와 같이 학습을 시킨 다음 feed-dict를 이용해 예측이 가능하다
Queue Runners
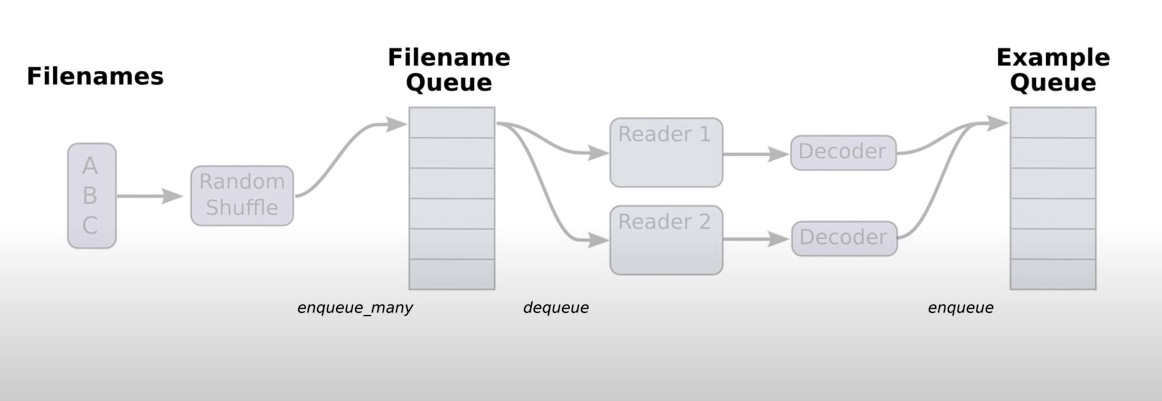
텐서플로우에서 만든 기능?
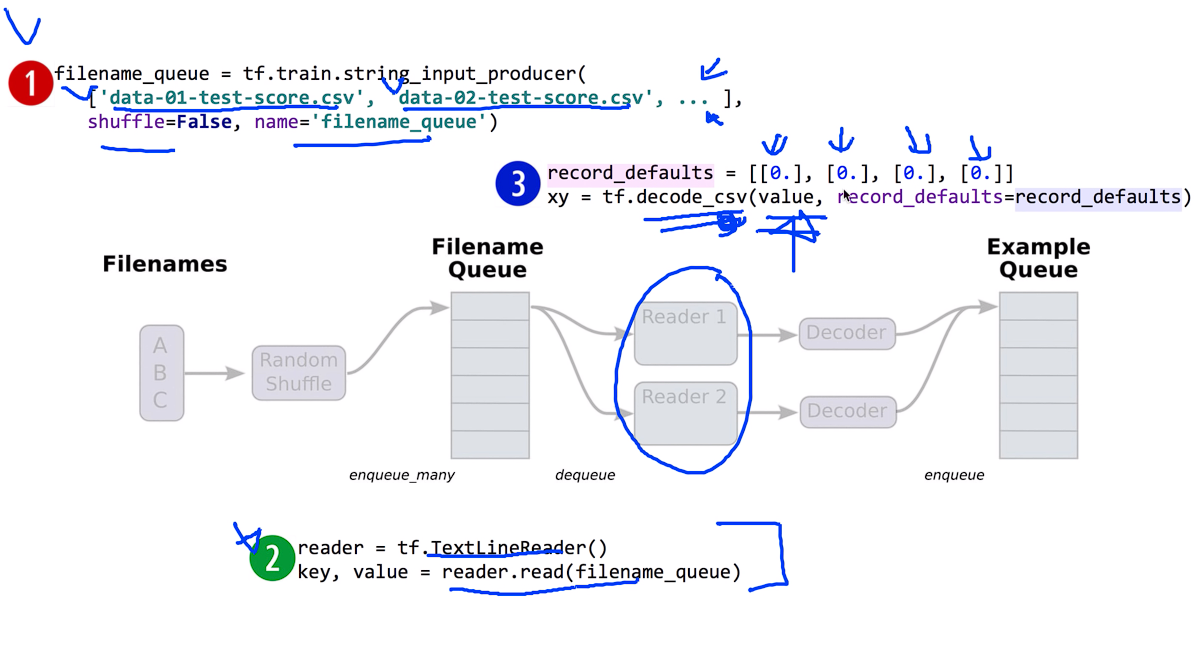
첫번째 스텝은 우리가 가지고 있는 파일들의 리스트를 만들어준다.
두번째 스탭은 이 파일을 읽어올 Reader를 정의해준다.
세번쨰 스탭은 value를 읽어와서 decode_csv를 이용해서 가지고와?
tf.train.batch

batch란 일종의 펌프?
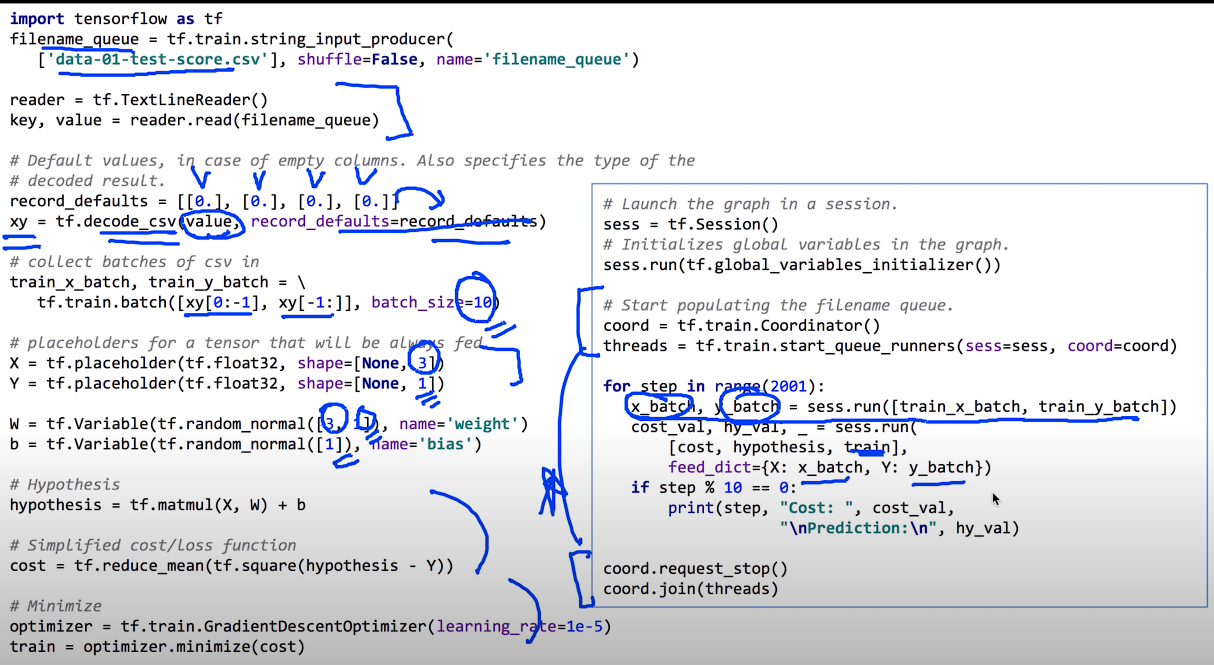
shuffle_batch

셔플 배치
