ML lec 5-1: Logistic Classification의 가설 함수 정의
Regression
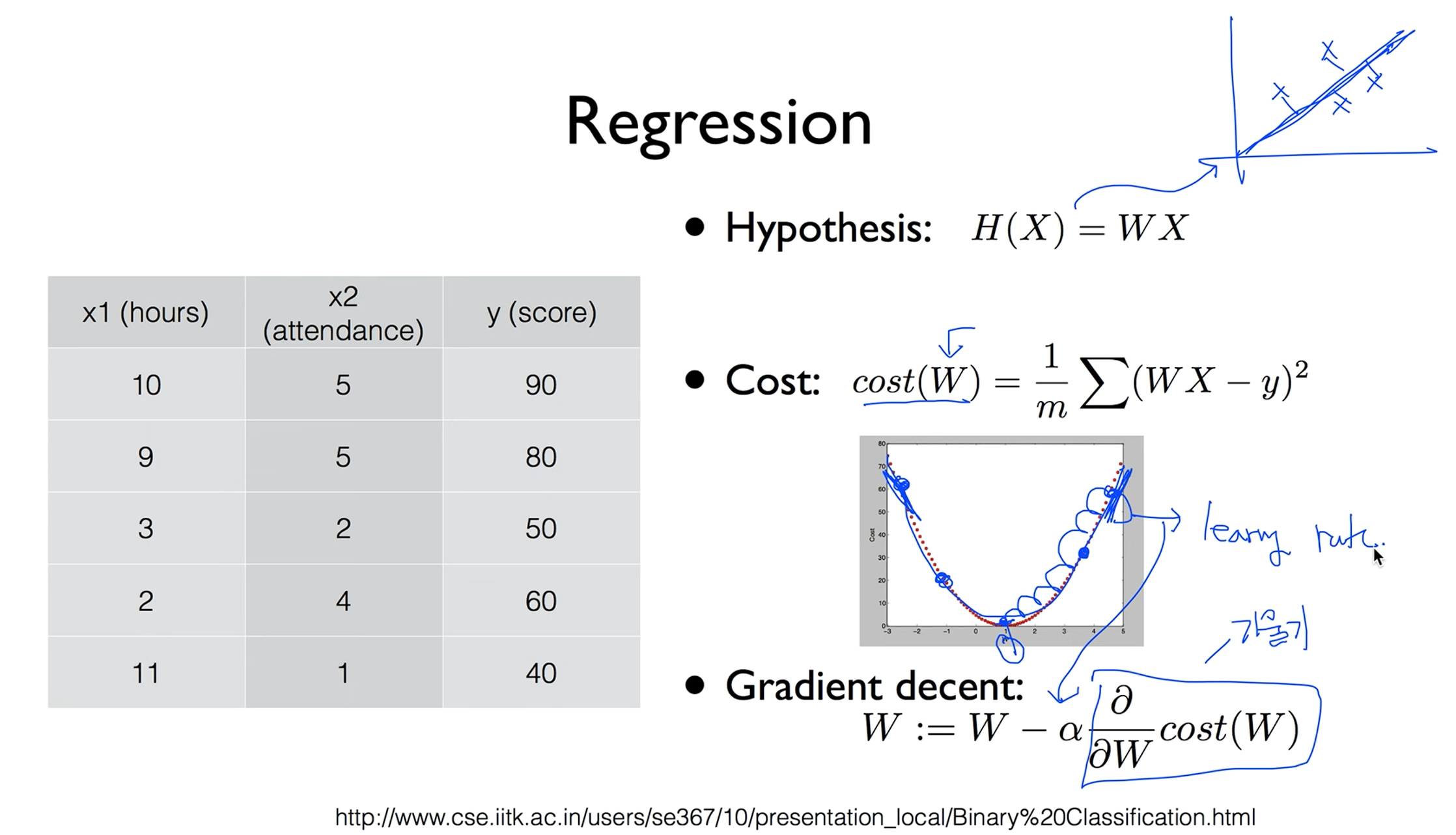
이전 시간에 배웠던 Regression에 대해 복습해보자.
Classification
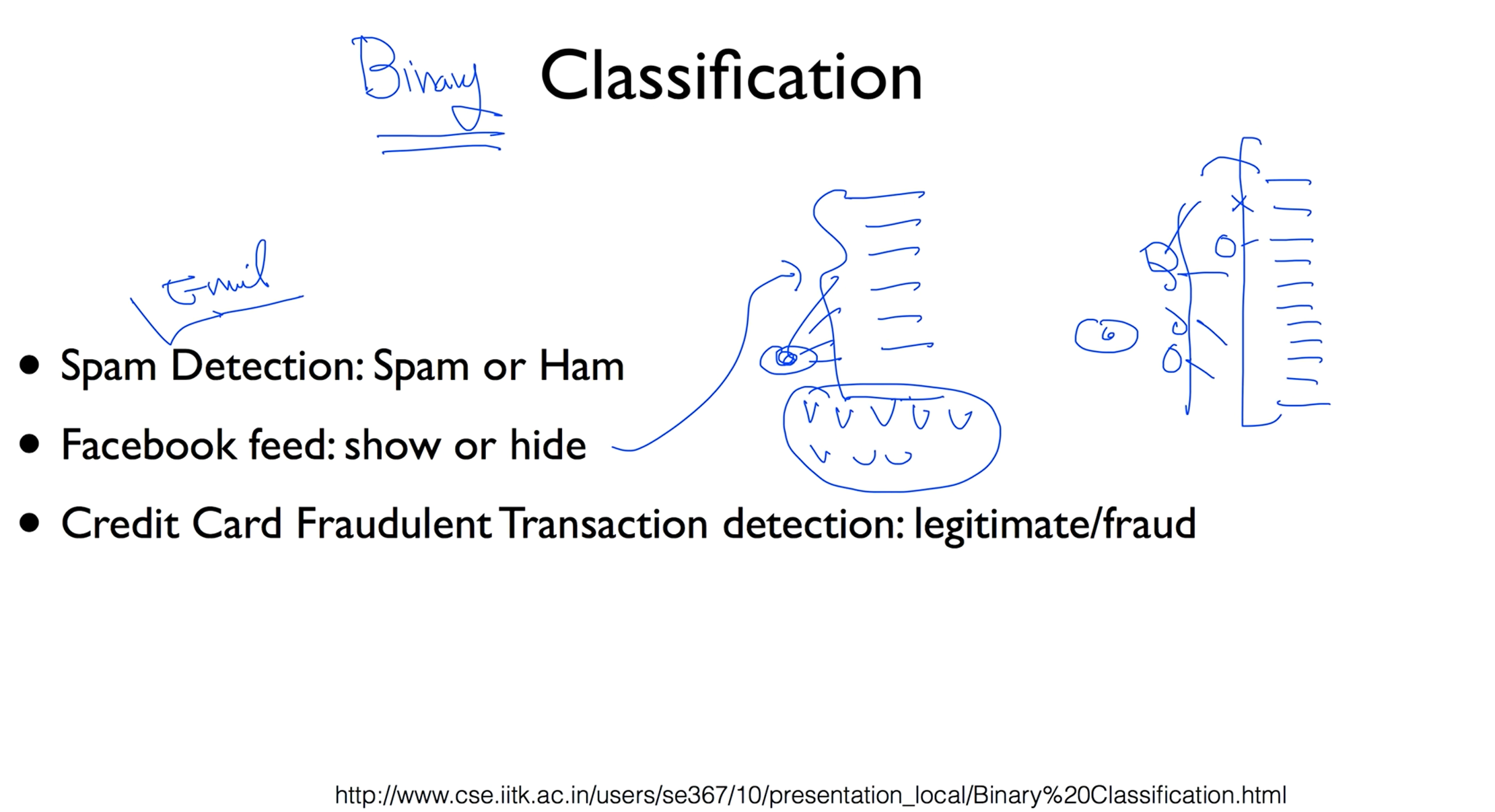
이전의 Regression은 숫자를 예측하는 것이였다면 Binary Classification은 두개 중 하나를 고르는 겁니다.
예로 스펨 메일인지 아닌지, 페이스북 피드에서 이전에 좋아요를 누른 기사나 타임라인을 학습해서 피드별로 보여줘야하는지 아닌지, 크레딧 카드 같은 경우도 기존의 구매 패턴을 학습해서 분실당했을때 기존과 다른 구매 패턴이 나왔을때 판단한다던지를 알려줍니다.
0, 1 encoding

이것을 기계적으로 학습하기 위해서 숫자 0 또는 1로 인코딩을 합니다.
Pass(1) / Fail(0) based on study hours
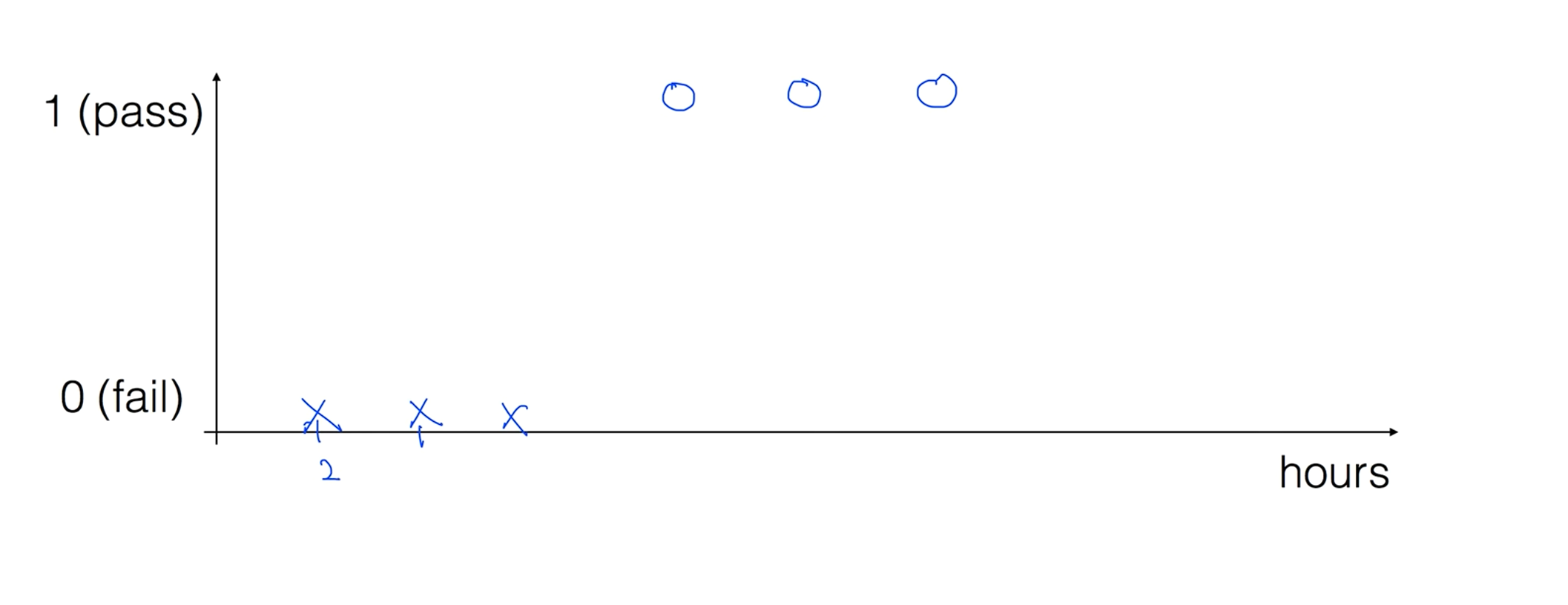
쉬운 예로 학생이 공부하는 시간에 따라 시험에 합격인지 불합격인지 0과 1을 예측하는 모델로 예를 들어보겠습니다.
Linear Regression?
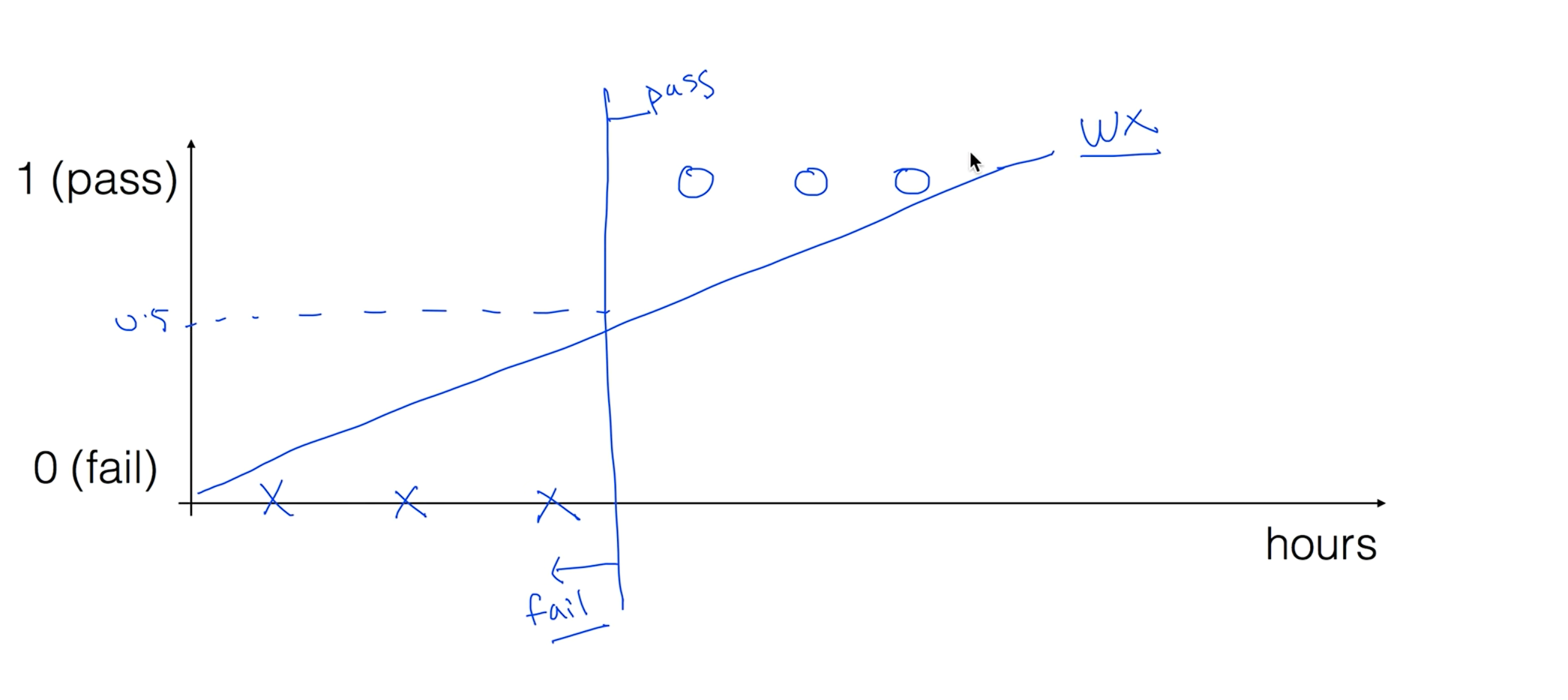
리니어 리그레이션으로 뭔가 할 수 있을것만 같다. 중간 지점이 0.5이니 중간지점을 잘라서 0.5보다 작으면 불합격 0.5보다 크면 합격으로 예측이 될거같다는 생각이 듭니다.

이 모델에 문제가 있따 우리가 가지고 있는 학습 데이터에서 50시간을 가지고 합격을 했다면 이상태에서 리니어한 모델을 학습을 시키면 선이 기울어집니다. 여기서 문제가 새로운 기준점으로 합/불을 판단하면 이전 데이터로 작성한 합격 데이터가 불합격이 되는 문제가 있다.
Linear regression

0보다 작거나 1보다 훨씬 큰 수가 나올 수가 있다.
Logistic Hypothesis

결과적으로 리니어 리그리션에서는 이 가설이 맞는데 0과 1사이로 압축을 시켜주는 가설이 있을까해서
이것을(H(x))을 z 로 두고 어떤 g라는 함수에 z의 값에 상관이 없이 0 ~ 1사이를 만들어주는 함수가 있을까 하면서 많은 사람들이 찾았습니다.
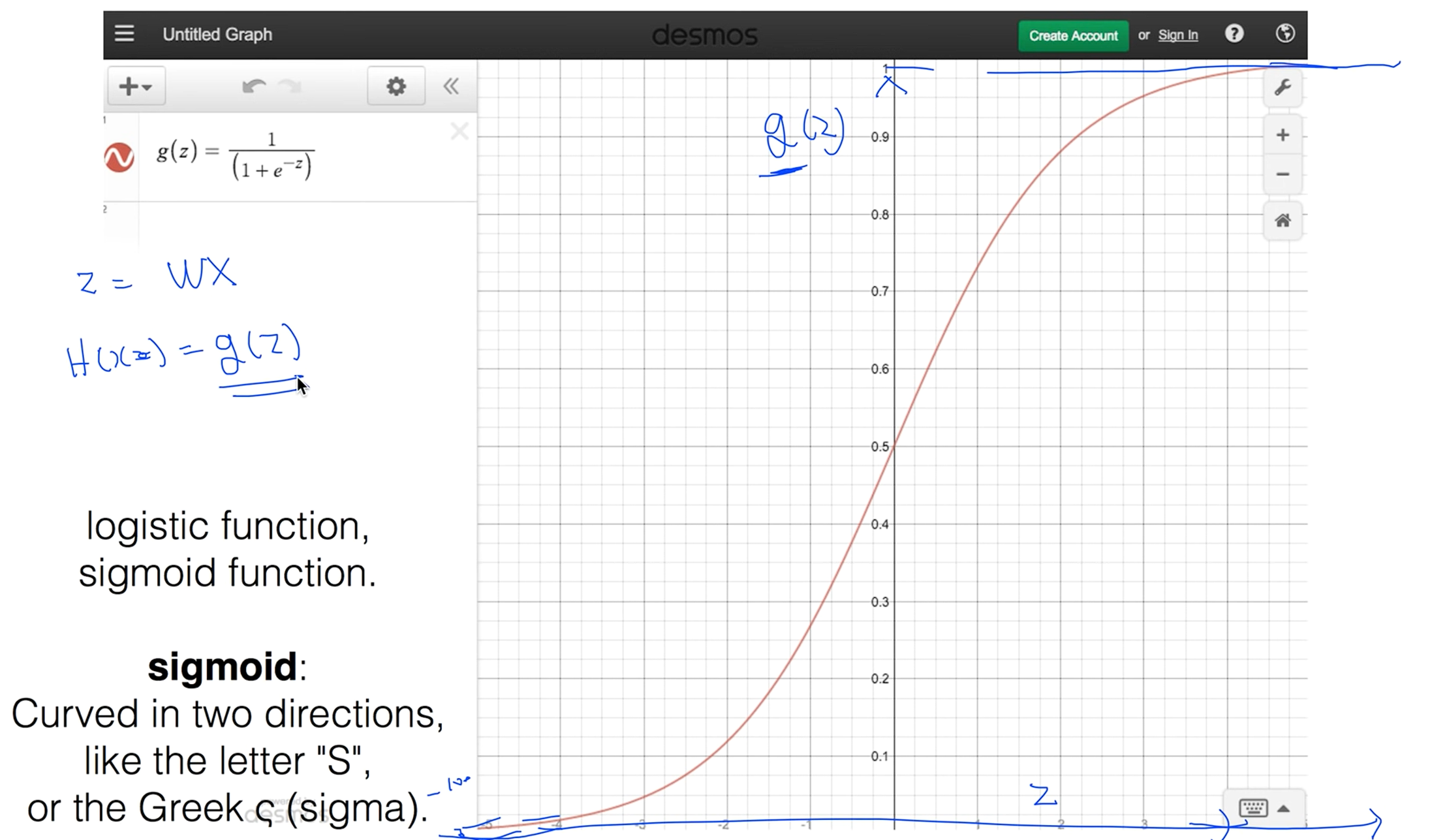
해서 사람들이 찾은게 g(z) = (1+(e의 -z승)) / 1 분모의 값이 1보다 작을거 같다. e의 -z 승이 0으로 가게되면 값이 1이 되고 그 값이 커지면 0으로 가는 이런 함수를 Sigmoid function라고 한다. 또는 logistic function이라 한다.
z값이 커지면 1에 가까워지고 z값이 작아지면 0에 가까이 수렴한다.
Logistic Hypothesis
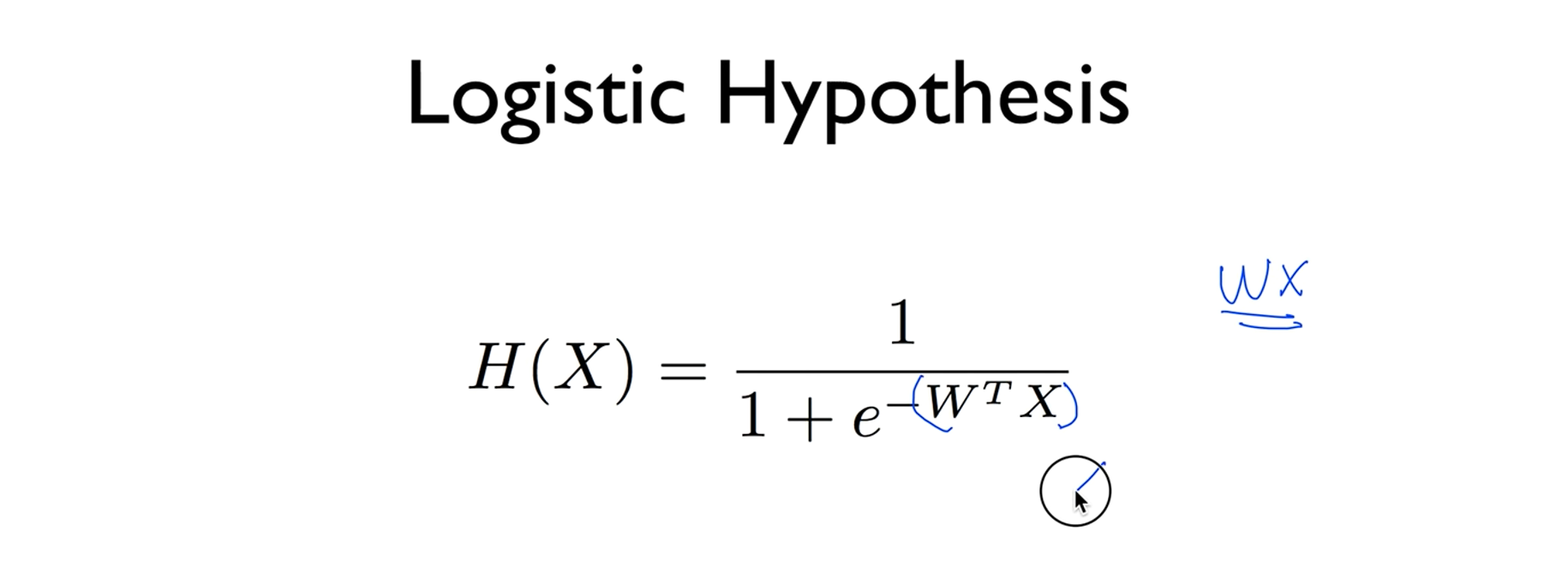
그래서 우리의 로지스틱 클래스 피케이션의 하이퍼퍼시스는 이렇게 주어집니다. 이것이 바로 시그모이드 함수였구요. 여기다가(W의 T승 x X) 우리가 가지고 있던 리니어 하이퍼퍼시스를 넣은것입니다,
ML lec 5-2 Logistic Regression의 cost 함수 설명
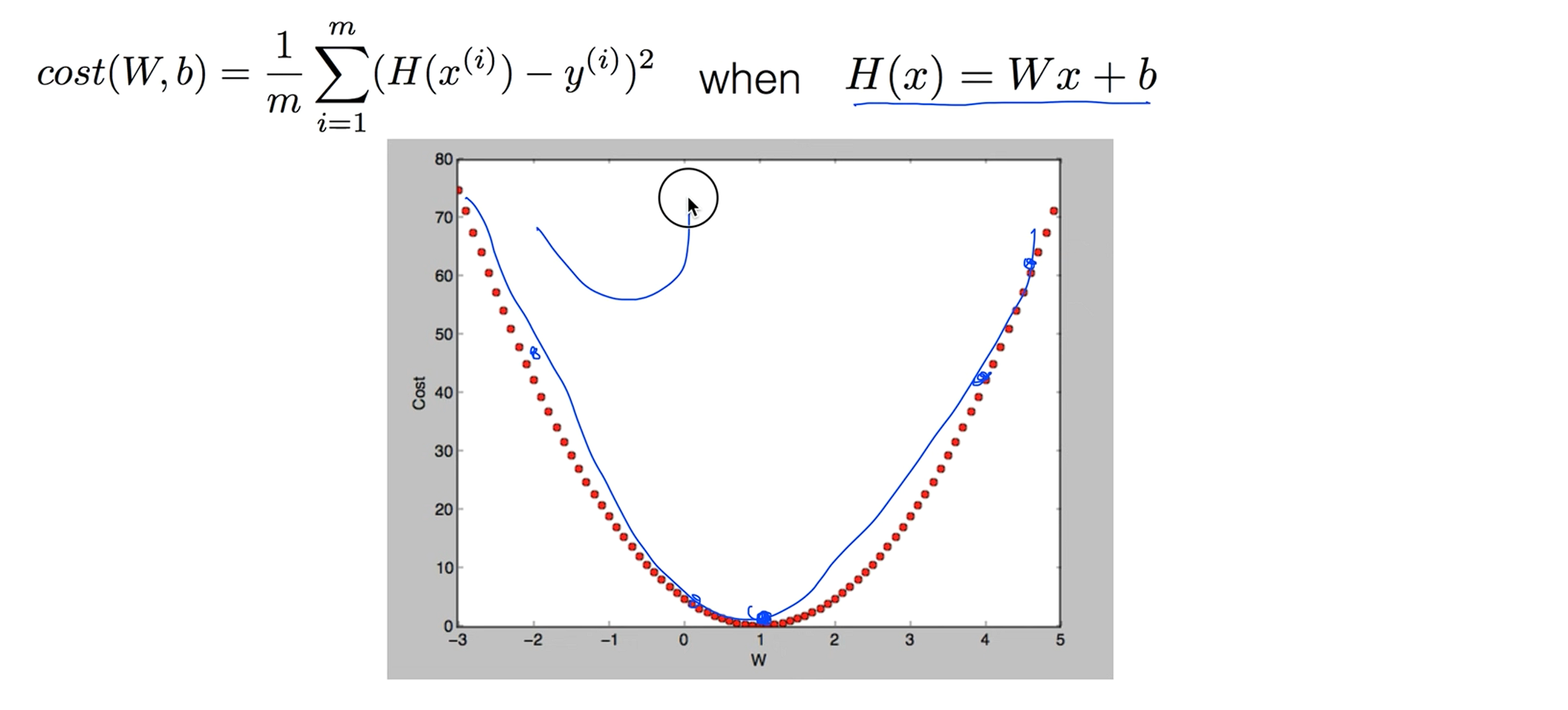
Linear regression의 하이퍼퍼시스로 Cost function을 그래프로 그려본다면 이런식의 밥그릇 모양이 나타났죠.
Cost function

그런데 우리의 가설(H(x))이 바뀌었기 때문에 시그모이드 함수를 사용해서 0 ~ 1이 들어오게 만들었기 때문에 이 가설을 사용해서 기존에 사용하던 cost function을 그래프로 그려보면 울퉁불퉁하게 나옵니다.
그 결과, 그레디언트 디센트 알고리즘을 사용하게되면 시작점이 어디에 있냐에 따라서 결과값이 달라 질수 있습니다. 이런 지점을 Local Minimum이고 우리가 찾고자 하는건 전체에서의 Minimum 즉, Global Minimum을 이라고 하는데 Global Minimum을 찾는게 목표인데 찾기가 힘들다.
그래서 우리가 H(x)를 바꾸듯이 Cost function값도 바꿔야 합니다.
New cost function for logistic
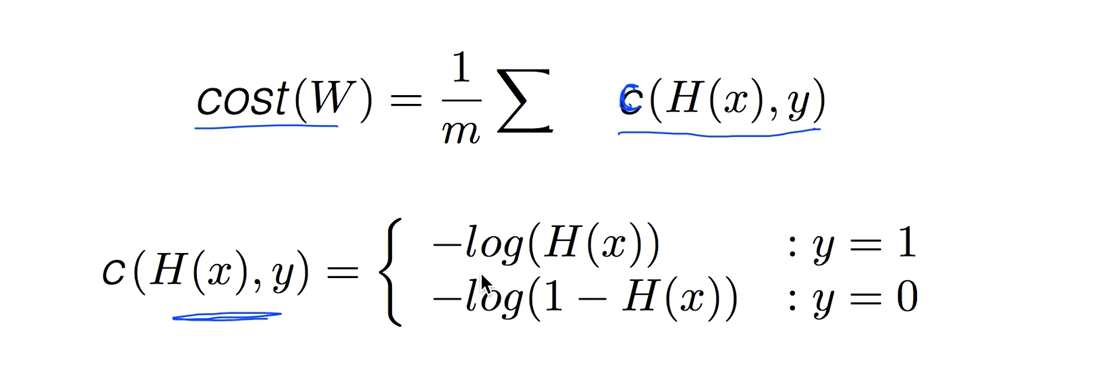
간단하게 코스트함수는 어떤값의 평균이니까 하나의 엘리먼트의 코스트를 구해서 평균내는걸 C함수라 합시다
C함수는 두가지 경우에 따라 함수를 정의하는데 y = 1일땐 -log(H(x)) y = 0일땐 -log(1-H(x))
Understanding cost function
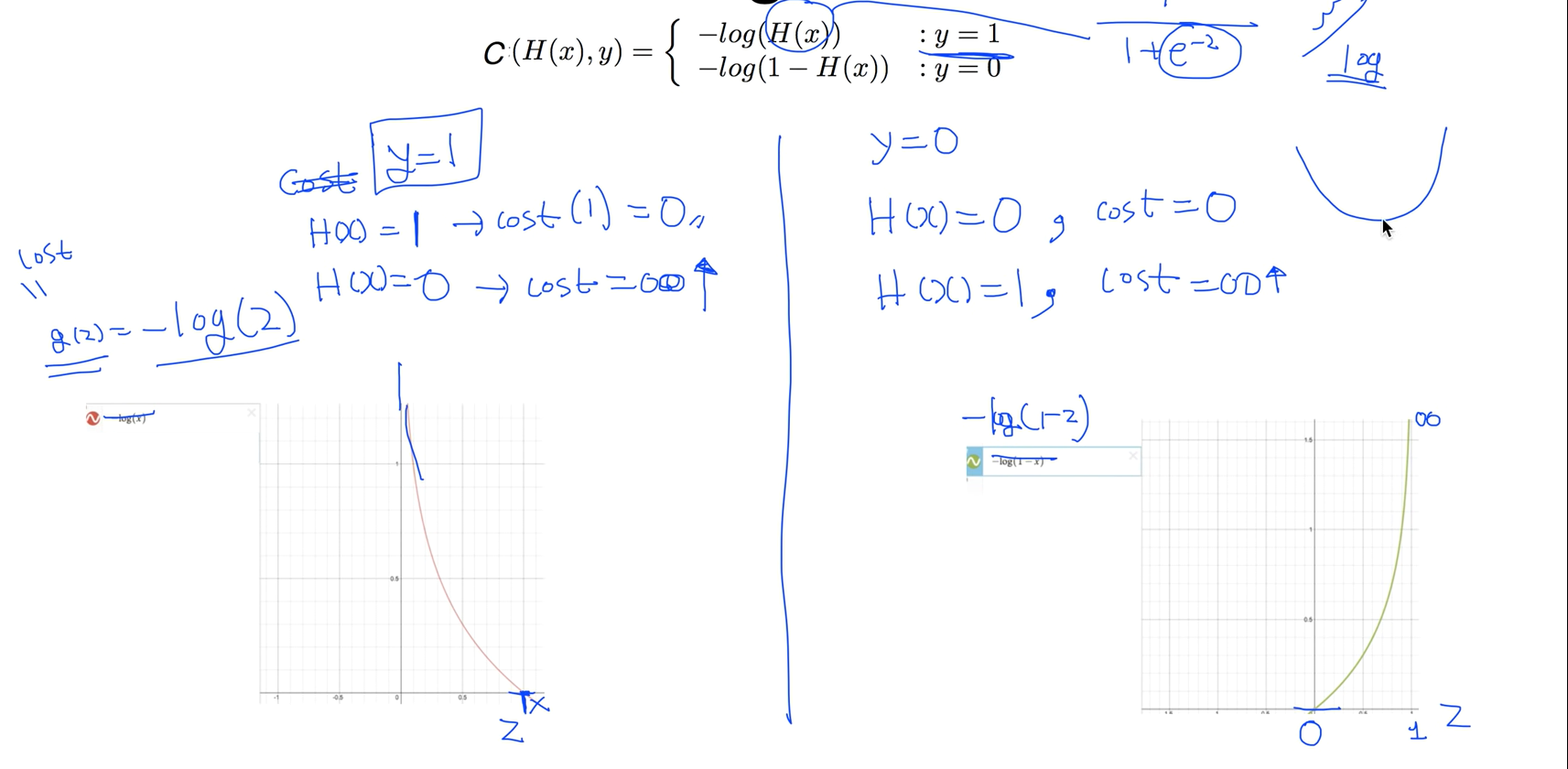
기존에 정의한 하이퍼퍼시스에서 (e -z승)이 들어가 있기 때문에 구부러진것을 만들게 되는데 이것과 상극이 되는게 log 함수 입니다.
log함수를 사용한다는것이 기본적인 아이디어 이고 실제로 log 함수의 모양을 보면 잘 맞는다 좌측 그림을 보면 g(z) = -log(z) 일때 z가 1인 경우에 이 함수는 0이 되고 z가 0에 가까워지면 이 함수의 값은 굉장히 커진다.
Cost function 의미 : 우리가 실제의 값과 예측한 값이 같다면 또는 비슷하면 코스트값은 작아지고, 예측한 값이 틀리면 코스트값을 크게해서 모델에게 벌을 주는 의미이다.
Interaction term : 자연 상수 e는 자연로그의 밑, 오일러의 수등 여러 이름으로 불리는데, 파이(π)처럼 수학에서 중요하게 사용되는 무리수이며, 그 값은 대략 2.718281.. 입니다.
Cost function
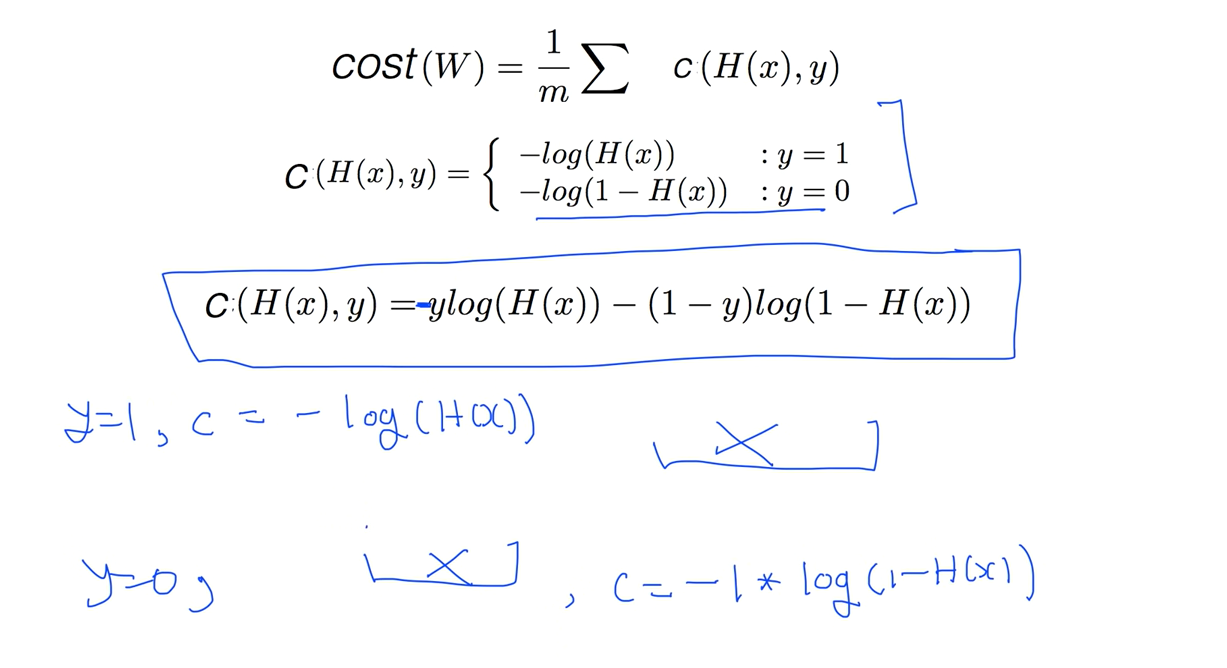
다시한번 정리해보면 cost를 전체의 평균으로 보고
하나의 y에 대해서 1일때 0일때 2개의 케이스를 가지고 코스트 함수를 각각 정리하면 잘된다. 허나 텐서플로우에서 코드로 구현할때 If문을 활용해서 코드를 짜야하니 복잡하다 이를 좀 더 쉽게 만든 식이 제일 아래에 있는 식이다.
Minimize cost - Gradient decent algorithm
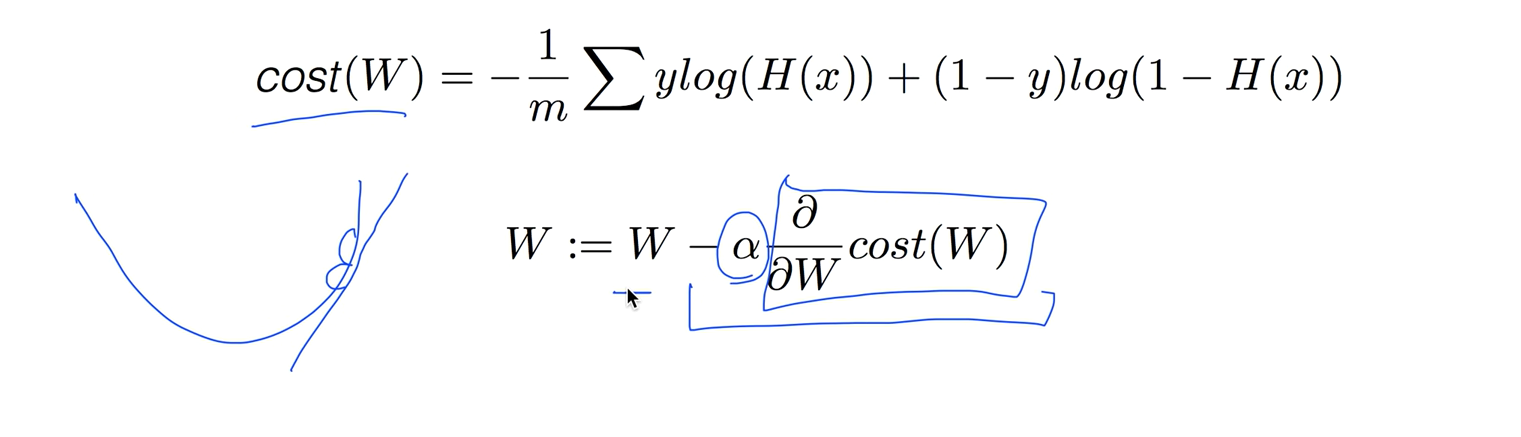
코스트가 주어졌으면 코스트값을 미니마이즈하는 것인데 cost 함수의 기울기(W)를 구할때는 미분을 해야하는데 우리는 그냥 알고리즘만 이해하고 미분은 컴퓨터가 알아서 해줄것이다.
Gradient decent algorithm

텐서플로우로 작성 시 코스트 값을 작성할 대 아래의 코드처럼 쓰고 Minimize 같은경우는 관련 라이브러리가 있어 쉽게 작성이 가능하다.
ML lab 05: TensorFlow로 Logistic Classification의 구현하기 (new)
Logistic Regression
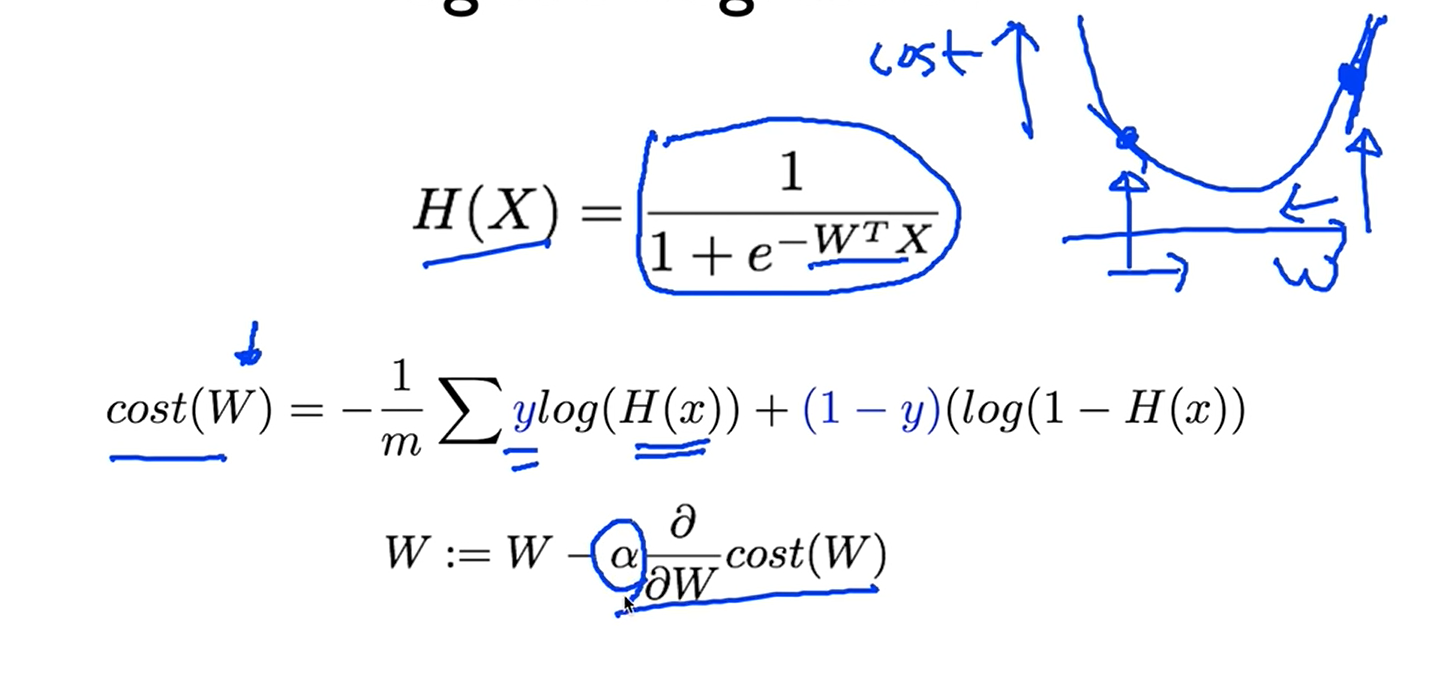
하이퍼퍼시스가 바뀌었기때문에 코스트를 구하는 계산도 바뀌었다.
Training Data (실습)
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
x_data = [[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]]
y_data = [[0], [0], [0], [1], [1], [1]]
# placeholders for a tensor that will be always fed.
X = tf.placeholder(tf.float32, shape=[None, 2])
Y = tf.placeholder(tf.float32, shape=[None, 1])
W = tf.Variable(tf.random_normal([2, 1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')
# Hypothesis using sigmoid: tf.div(1., 1. + tf.exp(tf.matmul(X, W) + b))
hypothesis = tf.sigmoid(tf.matmul(X, W) + b)
# cost/loss function
cost = -tf.reduce_mean(Y * tf.log(hypothesis) + (1 - Y) * tf.log(1 - hypothesis))
train = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(cost)
# Accuracy computation
# True if hypothesis > 0.5 else False
predicted = tf.cast(hypothesis > 0.5, dtype=tf.float32)
accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted, Y), dtype=tf.float32))
# Launch graph
with tf.compat.v1.Session() as sess:
# Initialize TensorFlow variables
sess.run(tf.global_variables_initializer())
for step in range(10001):
cost_val, _ = sess.run([cost, train], feed_dict={X: x_data, Y: y_data})
if step % 200 == 0:
print(step, cost_val)
# Accuracy report
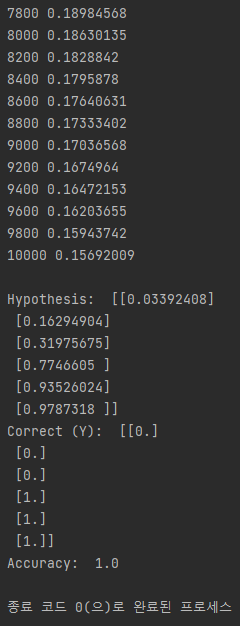
h, c, a = sess.run([hypothesis, predicted, accuracy], feed_dict={X: x_data, Y: y_data})
print("\nHypothesis: ", h, "\nCorrect (Y): ", c, "\nAccuracy: ", a)