해당 게시글은 LG Aimers Phase1의 수업 내용을 정리한 글로, 모든 내용의 출처는 https://www.lgaimers.ai/ 입니다.
Reinforcement Learning
MDP and Planning
-
강화학습
-
‘순차적 의사결정’ 문제를 담당하여 해결하는 프레임워크
- ‘순차적 의사결정’ : 일상에서 해결해 나가는 거의 모든 의사결정들이 해당함
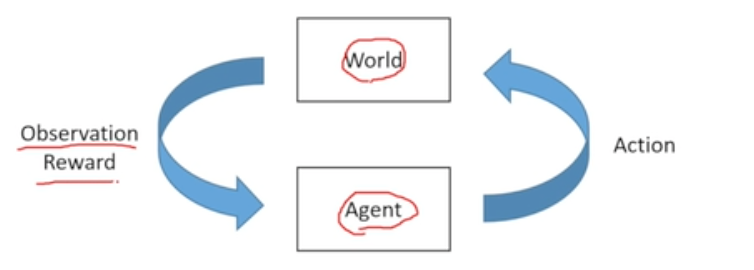
- 미래에 기대되는 보상의 합을 최대한하는 행동을 선택하는 것
- 내가 당장 행동을 해서 보상을 받는 것과 일련의 행동들을 통해 미래에 큰 보상을 받는 것을 비교
- ‘순차적 의사결정’ : 일상에서 해결해 나가는 거의 모든 의사결정들이 해당함
-
시행착오에 대한 수학적 formulation
-
-
MDP : Markov Decision Processes
- process : 시간에 따라 바뀌는 시스템에서 문제를 푼다
- descrete time을 가정하여 각 타임스텝마다 행동
- Markov : 의사결정을 내리기 위해 필요한 모든 정보를 관측할 수 있다
- 과거 이력, history를 볼 필요가 없음
- Decision : 단순하게 매 time step마다 행동을 한다
- 모종의 reward, cost 개념이 있어서 이를 최대, 최소화하는 것이 목표
-
Markov Process 설명

-
Markov Process
- State : 현재 상태
- Process : Transition 모델 - 현재 상태가 어떻게 바뀌어나가는가
- Markov Property : 현재 상태가 주어지면 과거의 이력에 독립적이다 (마르코프 성질)
- 유한한 상태 집합을 가지고 있다고 할때 Transition model을 매트릭스 형태로 나타낼 수 있음 ~ Markov Chain
-
Markov Reward Process : Markov Process + 보상
-
Reward Function : 현재 있는 state에서 주어지는 reward
-
discount factor :
-
Return (미래 보상합)에 관심 있음
- Random Variable임 ~ 미래 보상 합의 기댓값 : Value Function V(s) - 각 상태의 가치를 value function으로 정의 가능 ~ : recursive function
- : 현재 state에서의 reward
- : discounted sum of future rewards
- Bellman Equation이라고 불리움
- Random Variable임 ~ 미래 보상 합의 기댓값 : Value Function V(s) - 각 상태의 가치를 value function으로 정의 가능 ~ : recursive function
-
현재 받는 reward : ~ 미래에 받을 reward :
-
H : horizon ~ 어느정도의 미래까지 볼 것인지 ~ 무한대까지 사용 가능
-
주로 infinite horizon 상황에서 다룰 것
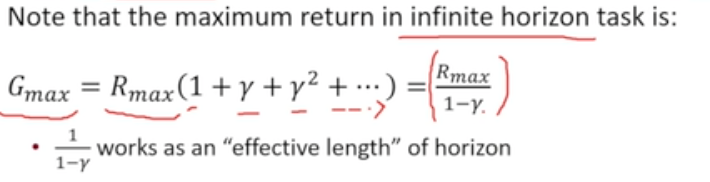
- infinite horizon을 가정하더라도 유효한 horizon의 길이 =
-
-
미래의 보상을 감쇄 (discount)하기 위한 값이 값
-
-
수학적 편의성 가짐
-
사람들이 현재의 보상을 더욱 중시하기에 이러한 태도 반영 가능
-
-
-
Markov Property : 현재 보상을 받는 것 또한 과거의 이력에 독립적이다.
-
Iterative Algorithm : 역행렬을 통해 푸는 방식보다 간단히 문제 해결 가능
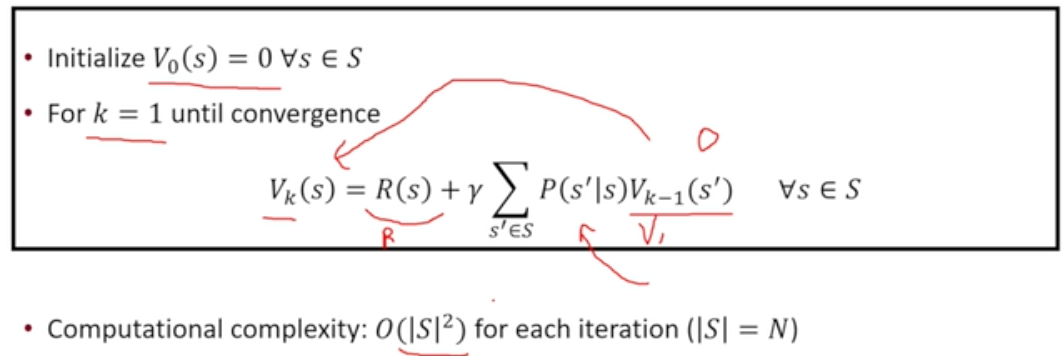
- Dynamic Programming
- 단계별 값을 저장하여 현재의 값을 계산하기
- 기존의 value function + 현재의 reward
- Dynamic Programming
-
-
Markov Decision Process : Markov Process + 행동
-
MRP : 보상 개념은 있으나 행동 개념이 없음 → 행동 개념 추가
-
MDP&MRP : 사전에 정의된 전이모델에 따라 행동없이 상태 변화 → 행동에 기반하여 상태가 변화
-
Markov Property : 보상, 상태, 행동 모두 과거 이력에 대해 독립적이다.
-
MDP Policy를 찾아내는 것이 최종 목표
- 각 state에서 어떠한 action을 취할 것인가
- 학습하고 싶은 agent의 행동을 전체적으로 정의
- stationary하게 행동을 정의함 ~ 상태에 따라서만 행동을 함
- deterministic policy : 상태의 함수로서 행동이 나오는 형태
- stochastic policy : 상태에 따라 행동이 어떠한 확률분포로 나오는 형태
-
policy가 주어진다면
- MRP에서 사용하는 보상함수, 전이함수 활용하여 문제 풀이 가능
-
Policy Evaluation Algorithm
-
MRP에서 Value Function을 구하는 방식과 동일
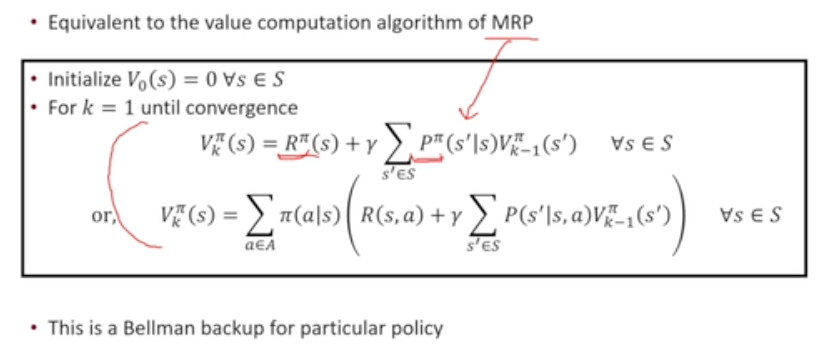
- 정책이 주어져 있을 때, 정책이 불러올 수 있는 기대 보상의 합(V)을 계산 가능
- 기대 보상의 합을 통해 정책의 가치를 비교, 평가 가능
-
-
Optimal Policy
- 반드시 존재해서 모든 다른 policy와 비교하여 좋거나 같은 policy(가 존재한다.
- 해당 policy를 성취하는 value function은 딱 한 개 존재하여 해당 value function을 optimal value function이라고 할 수 있다.
-
-
- process : 시간에 따라 바뀌는 시스템에서 문제를 푼다
-
Policy Search
-
Policy Iteration

→ 어떤 MDP가 주어졌을 때, 가정
→ 에 해당하는 value function 구하고 이에 기반하여 policy를 더 좋게 만들음
-
State-Action Value Q
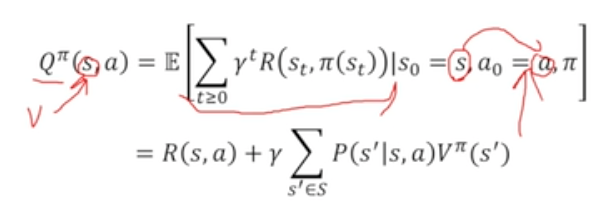
-
미래 감쇄 보상합의 기대값
-
State에서 어떤 행동을 한다 까지 주어져있는 상황에서의 가치 함수
-
각 행동의 가치를 더 확실하게 알 수 있기 때문에 Q 활용
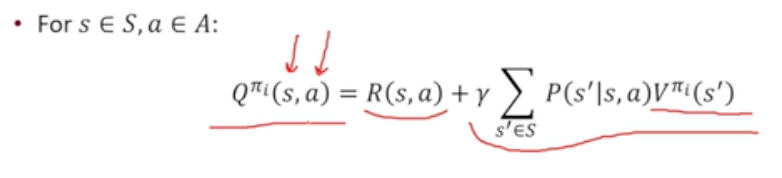
-
Policy Improvement : Q를 최대화하는 action을 찾게되면 현재 policy보다 좋은 policy임
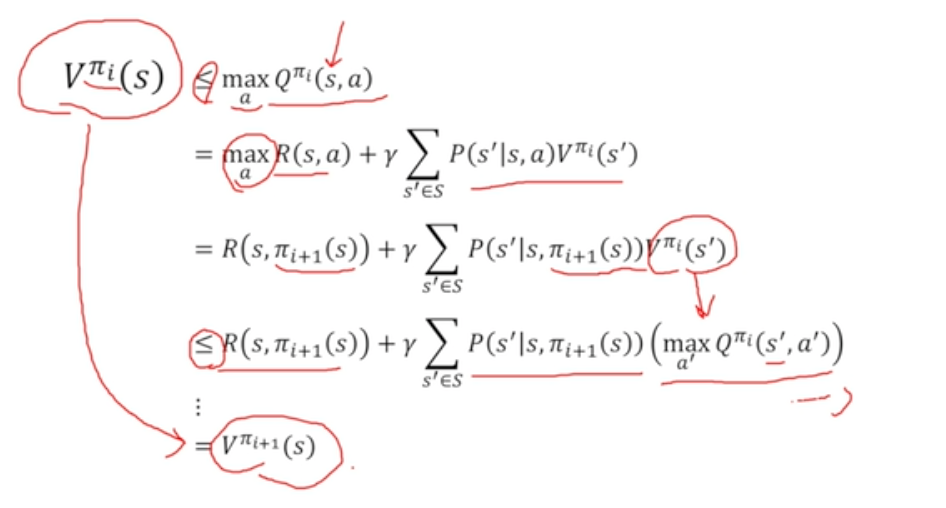
- PI 알고리즘을 진행했을 때 얻어지는 policy가 항상 이전 policy보다 좋아짐
- 이를 활용하면 무조건 optimal policy에 도달할 수 있게 됨
-
-
Optimal Bellman Eqation

-
max연산이 있기에 matrix 활용한 계산 불가능
-
이를 활용하여 DP를 돌리면 Value Iteration

- 로 수렴할 것이라는 가정 하에 를 최대화하는 a를 찾아내면 이를 활용하여 Bellman Optimality Equation을 풀어내는에 해당하는 를 찾아낼 수 있음
-
-
-
Value Iteration vs Policy Iteration
- Value Iteration :
- Policy Improvement step이 없음
- 매 step의 value iteration할 때 마다 optimal policy step의 value에 해당하는 Policy를 얻게 됨
- 매 step의 reward를 더하는 형태 - 각 step의 value iteration은 horizon이 k일 때의 optimal value function이다.
- finite horizon의 optimum policy를 매 step마다 계산을 해가며 infinite horizon문제의 optimum policy를 계산해 나가는 문제이다
- Policy Iteration
- Policy Evaluation을 통해 어떤 policy에 해당하는 infinite horizon value를 얻어내고 그것의 policy를 개선하고 이를 반복하는 알고리즘
- Value Iteration :
-
Model-Free Policy Evaluation
- 샘플이 주어져있을 때 어떻게 Policy Evaluation할 것인가
- MDP에 관련된 실제 정보가 없을 경우에 (전이모델, 보상모델 정보가 없을 때) 정책의 예상되는 return을 어떻게 계산할 것인가
-
Monte Carlo Policy Evaluation
-
여러번의 관측을 통해 평균을 취하는 법
-
return을 여러번 시행하여 평균값 취하기
-
Value는 Return의 평균이다
-
장점 : MDP의 전이모델, 보상모델을 필요로하지 않음 + Markov 성질 또한 필요로하지 않음
-
단점 : finite horizon MDP, terminal state가 있어서 반드시 끝이 있는 episode에서만 계산 가능
-
종류
-
First-Visit MC : Trajectory를 진행하며 처음 만나는 state에 대해서만 return을 value function으로 활용
- 나중에 만났을 때 발생하는 return은 value function에 영향 미치지 않음
- 장점 : Unbiased 알고리즘 (+consistent)
-
Every-Visit MC : Trajectory를 진행하며 만나는 모든 state에 대해서 return을 value function으로 활용
- G 샘플의 개수가 매우 많아짐
- 장점 : variance가 낮은 estimator를 가지게 됨 (+consistent)
- 단점 : biased estimator ~ return 간의 corelation이 존재하여 bias 발생
-
Incremental MC : return estimator를 얻어내고 평균을 내는 과정에서 incremental 수식을 활용할 수 있음

- 1/N(s)대신 (learning rate) 활용 가능
- : 평균이 아니라 최근 잔차에 더 큰 가중치
- 그렇지 않으면 예전 잔차에 더 큰 가중치
- 1/N(s)대신 (learning rate) 활용 가능
-
-
Diagram
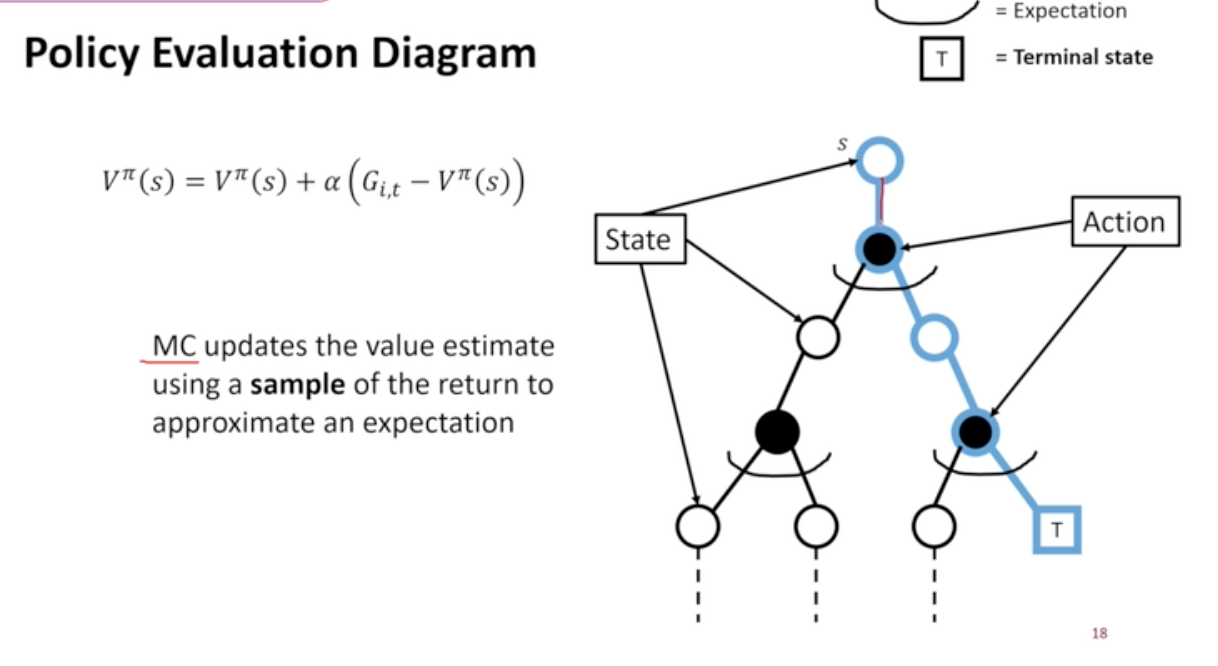
- MC : 한 줄기를 따라 내려와 Trajectory Sample 진행
- 이 경로를 통해 V_pi를 업데이트
-
단점
- high variance estimator
- variance를 줄이기 위해서는 상당히 많은 데이터가 필요함
- trajectory를 구하기 어려울수록 실제 적용이 어려움
- terminal state에 도달해야만 return 계산 가능
- episode가 무조건 종료되는 episodic setting에서만 MC 알고리즘 적용 가능
- high variance estimator
-
-
Temporal Difference 0 Learning
-
강화학습에서 가장 중요한 알고리즘
-
MC 장점 + DP 장점
-
MDP 모델이 필요 없음
-
infinite horizon을 가지거나, episode가 끝나지 않아도 사용 가능
-
목표 : V_pi 계산
- Bellman Operator 활용
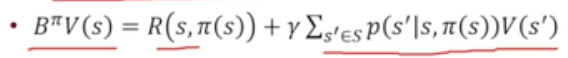
- return 대신 Bellman Operator를 활용한 것을 G_t대신 사용하자 - approximation

- Bellman Operator 활용
-
과정

-
-
MC vs TD (예시)
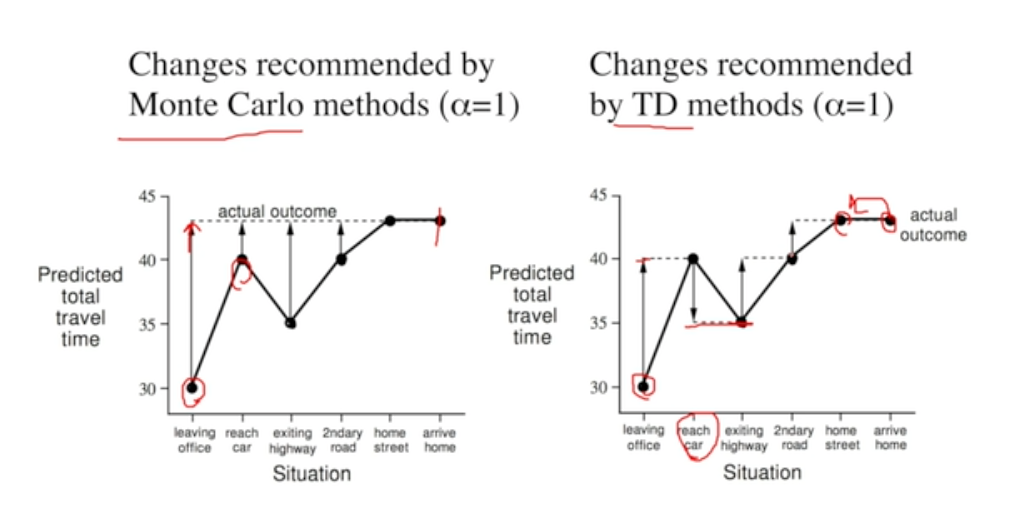
- MC : 모든 episode가 45분에 마무리되는 것을 알고 있으므로 모든 step에 대해 마지막 state인 45분에 맞춰 update
- TD : 각 step에서 다음 step의 value function을 가지고 update
- 점의 위치가 변화한 뒤 해당 위치에 맞춰 다시 update … 반복
- 장점 :
- episode가 끝나기 전에 update 가능 (학습 빠름)
- episode가 끝나지 않아도 update 가능 (보다 넓은 범주의 문제 해결 가능)
- Bootstrap & Sampling 두가지 모두 적용
-
DP for policy Evaluation → Certainty Equivalent Learning
- Reward, Transition 모델을 데이터 기반으로 학습하여 DP 돌릴 수 있지 않을까?
- MDP 모델을 알고 있지 않지만 샘플들을 이용하여 Reward, Transition 모델 학습

- Model Based algorithm!!
- cf) Model Free algorithm = MC, TD
- 매 업데이트마다 MLE모델을 얻어야하고 Planning해야 함 - 계산량 많음
- 그러나 기존 방법에 비해 데이터를 가장 효율적으로 사용 가능
- 데이터가 무한히 제공되면 solution을 반드시 찾을 수 있음 (consistent)
- Markov 가정 필요
-
모델 간 비교

-
모델 variance, bias 비교
-
MC : unbiased estimator, higher variance, consistent, 초기값에 민감하지 않음 (초기 value 없음 - return의 평균), 사용이 간단함
-
TD : biased estimator, lower variance, consistent, 벡터 형태의 value function을 가정하면 실제 true value로 수렴하게 됨 (뉴럴 넷과 같은 추가적인 approximation을 사용하게 된다면 실제 true value로 수렴하지 않은 경우 발생), 효율적, 초기값에 민감
-
학습 과정 비교
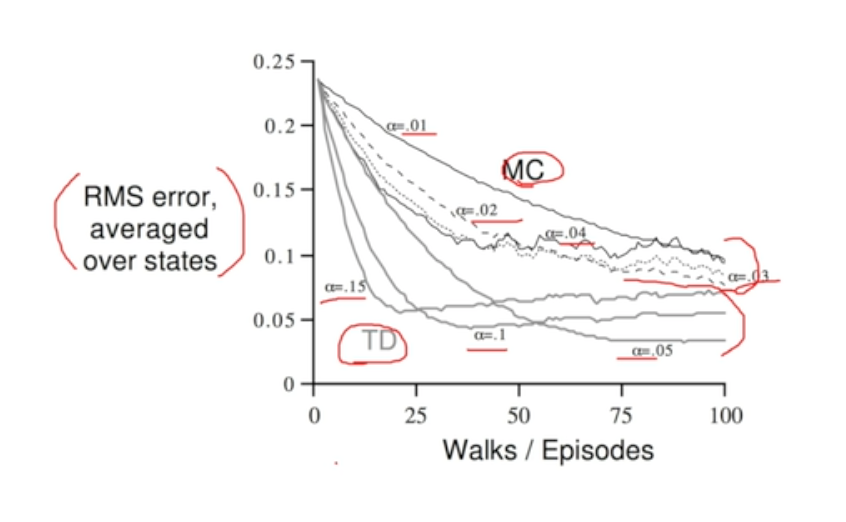
- MC가 더 많은 error 보임
- MC의 error 안정적으로 줄어듬 (오르락 내리락 하지 않음)
-
-
Batch MC & TD
-
유한한 데이터셋을 가지고 있을 경우

- MC와 TD로 얻어지는 value에 약간 차이가 발생함
- state A에서 MC : reward 0밖에 없음
- state A에서 TD : 다음 state인 B의 value를 가져와 0.75의 reward 발생
- MC와 TD로 얻어지는 value에 약간 차이가 발생함
-
-
Data efficiency & Computational efficiency
- 가장 간단한 형태의 TD : 하나의 샘플을 가지고 V(s) 한번 업데이트
- 각 update마다 상수의 computation 필요
- 길이 L짜리 episode가 있다면 → O(L)의 computation 필요
- Markov Struncture 활용하므로 해당 property에서 나오는 정보들을 효과적으로 활용
- DPCE 또한 가지는 장점임
- MC
- episode가 끝났을 때 나오는 return들이 L개 존재
- return L개를 가지고 value function을 계산 → O(L)의 computation 필요
- 미래에 모든 것을 한번에 update 하기 때문에
- TD보다 data efficient한 경우 많음
- 가장 간단한 형태의 TD : 하나의 샘플을 가지고 V(s) 한번 업데이트
-
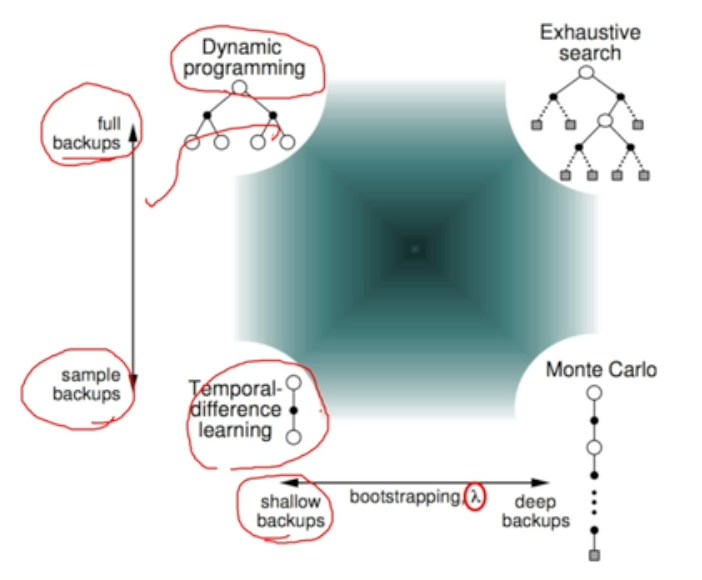
Bootstrapping & Sampling
- Bootstrapping : value evaluation할 때 기존의 estimator을 가지고 update를 하느냐
- MC : does not bootstrap
- DPCE & TD : bootstrap
- Sampling : expectation을 계산할 때 sample을 활용하느냐
- MC & TD : sample
- DPCE : dose not sample
→ TD의 경우 bootstrapping & sampling 모든 approximation을 활용하는 형태로 가장 극단적으로 효율성을 추구하는 형태
- Bootstrapping : value evaluation할 때 기존의 estimator을 가지고 update를 하느냐
-
Model-Free Control
-
실제 policy optimization이 진행되는 단계
-
정책을 어떻게 얻어낼 수 있을 것인가
-
true dynamics와 true reward model이 없을 때 → policy evaluation & improvement를 어떻게 할 것인가
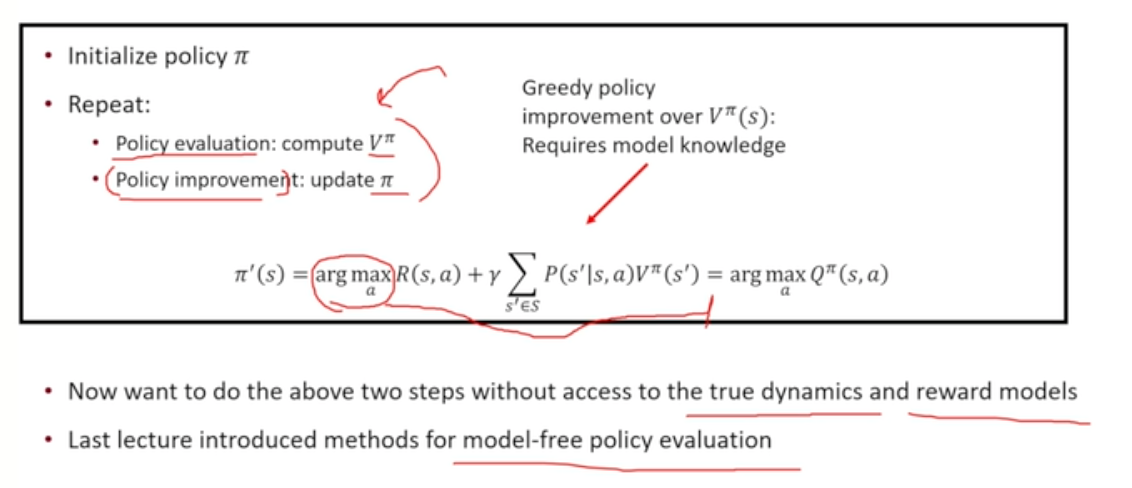
- model free evaluation을 통해 얻은 결과를 V_pi에 적용하여 기존과 유사한 방식으로 진행
- V에 대한 policy improvement가 불가능 → 대신 Q에 대한 policy improvement
- policy evaluation 또한 Q에 대해 학습 진행
-
Problem of Exploration
-
실제로 action을 해보기 전에 action의 여파를 예측하기 어려움
-
여파를 알기 위해 새로운 행동들을 수행하게 된다면 과거 좋았던 시도를 하는 데에 더 적은 시간을 들이게 됨
-
여러 탐험을 하느라 기존에 좋았다고 생각했던 행동을 덜 하게 됨
-
우리가 생각한 것 보다 더 적은 reward를 얻게 됨
-
모르는 상황에 대한 정보를 얻기 위해 얼만큼의 자원을 exploration에 투자할 것인가
-
관련 개념
- explore : 새로운 상황 탐색
- exploit : 기존에 좋다고 알려진 상황 수행
-
관련 알고리즘
-
Epsilon-greedy 알고리즘
-
exploration과 exploitation 밸런싱을 해결하는 가장 간단한 알고리즘
-
모든 행동이 0이 아닌 확률로 진행됨 (epsilon)
-
Q에서 optimal action을 할 확률 : (|A| : action 개수)
-
Q에서 optimal하지 않은 action을 할 확률 :
-
policy improvement theorem 동일하게 적용됨
-
기존 exploration의 문제를 어느정도 해결해내는 알고리즘
-
MC policy evaluation과 단순하게 함께 활용될 경우 - 필요로 하는 샘플, 시간의 양 상당하다는 문제 발생
- evaluation을 끝까지 않고 improvement를 진행
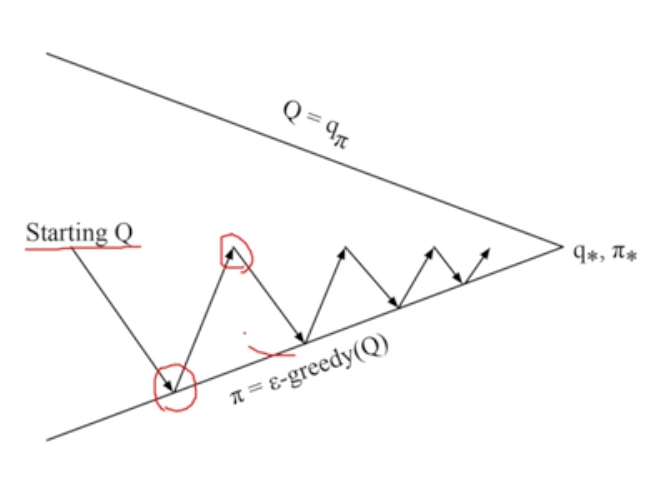
- generalized MC control algorithm으로 불리움
- 이를 활용하면 optimal policy로 수렴함 (일정 조건 만족시)
- evaluation을 끝까지 않고 improvement를 진행
-
Greedy in the Limit of Infinite Exploration (GLIE)
- Epsilon-greedy policy만을 활용하면 Epsilon probabilty 때문에 마지막에 random action하게 되므로 마지막에 optimal policy라고 말할 수 없음
- 이를 해결하기 위해 조건 필요
- time step을 무한히 갔을 때, state횟수가 무한대로 가게 되고 1의 확률로 greedy policy로 수렴한다
- epsilon을 1/i로 두고 스케일링 진행 : GLIE strategy
- GLIE 조건을 만족하지 않으면 충분히 많은 정보를 얻지 못해 부정확한 Q 함수를 얻게 되고 이를 활용해 얻어낸 policy가 optimal하다고 말할 수 없음
-
TD learning을 활용할 경우

- MC에 비해 variance가 작고 episode가 끝날때까지 기다리지 않아도 됨
- Q를 TD learning을 통해 구하고 Epsilon-greedy 알고리즘을 통해 policy improvement하며 GLIE 조건을 만족하도록 스케쥴링
- Q_pi를 converge할 때까지 update하지 않고 단 한번의 TD update만으로도 policy improvement 시도 가능
- 매 step마다 policy update - 훨씬 더 유연함
- SARSA algorithm

- s, a, r, s와 함께 a_{t+1}까지 활용하기에 SARSA 알고리즘으로 불리움
- Q function을 update하기 위해 TD를 활용하기에 다음 step의 action이 target을 계산하는 데에 필요
- Q update이후 pi update 진행
- theorem

- robbins-munro 조건 : stochastic approximation (lr을 두고 잔차만큼 update하는 방식) 알고리즘이 target의 기댓값으로 수렴하기 위한 기본조건
-
-
-
Q-Learing 알고리즘
-
policy improvement 단계를 별개로 두고 있지 않음
-
value iteration에 해당하는 알고리즘
-
Bellman optimality backup equation을 통해 optimal state action value를 찾아나가고 이 과정에 있어 policy가 구체적으로 도출되게 되는 과정
-
off-policy learning 알고리즘
- Bellman optimality backup를 통해 Q*를 직접 update하게 되며 여기에 필요한 sample들은 optimal policy일 필요가 사라지게 됨
- value를 estimate하는 policy(target policy)와 실제 action하는 policy (behavior policy) 사이의 괴리 존재

- 학습을 할 때 target policy에서 나온 데이터가 필요하지 않음
- 기존에 다른 policy에서 나온 경험, 데이터를 재사용하여 현재 value function을 학습하는 데에 활용 가능
- 데이터의 활용성 크게 늘어남
- exploratory policy를 통해 optimal policy를 얻어낼 수 있음
- 하나의 policy를 통해 학습하나 동시에 여러 policy의 value function을 학습할 수 있음 → 유연한 알고리즘의 설계가 가능해짐
- 실제로 행동하는 것을 관측하며 별개로 학습
-
cf) SARSA
- policy iteration - policy evaluation + policy improvement
- on-policy learning 알고리즘 - 단 하나의 policy 존재
- value를 계산하는 policy와 action하기 위해 사용하는 policy가 동일
- 직접적으로 경험을 얻어냄 / 실제로 행동하며 학습
-
Importance Sampling
- 기댓값을 취할 때 다른 분포에서 나온 sample을 가지고 기댓값을 취하는 방식
- P라는 샘플이 없을 경우 Q 샘플을 활용하여 확률에 대해 조정하면 원하는 샘플에 대한 보정값을 얻어낼 수 있음
-
TD
- MC에 비해 수월함 - 한 step에 대해서만 important sampling correction term을 넣어주면 off-policy TD learning을 할 수 있음

- MC sampling 보다 훨씬 더 적은 variance 가지게 됨
- MC에 비해 수월함 - 한 step에 대해서만 important sampling correction term을 넣어주면 off-policy TD learning을 할 수 있음
-
Q-learing
-
No importance sampling is required

- TD learning을 V가 아니라 Q에 대해 진행하게 된다면
- Q에 action dependent하기 때문에 action이 어떤 Policy에서 나왔던 간에 TD learning을 하면 좋은 Q로 가게 됨
- 현재의 policy action에 대해서는 다른 Policy()에서 나와도 되지만 next step의 policy a’에 대해서는 원래의 Policy()에서 나와야 Q에 대한 TD를 진행하더라도 로 수렴하게 됨
- importance sampling을 진행할 필요가 없어짐
- TD learning을 V가 아니라 Q에 대해 진행하게 된다면
-
과정


- SARSA에서는 Q가 TD target을 활용했음
- Q-learning에서는 Q에 대한 Bellman optimality backup equation을 가지고 TD learning 알고리즘을 유도한 것과 동일해짐
- 알고리즘 pseudo code
 → 코드에서 보이는 policy는 밖에 없으나 → Update Q 라인 중 Q-learning에서 학습되는 Q 자체가 optimal policy (혹은 모종의 policy(를 estimate하고 있는 Q이기 때문에
→ 코드에서 보이는 policy는 밖에 없으나 → Update Q 라인 중 Q-learning에서 학습되는 Q 자체가 optimal policy (혹은 모종의 policy(를 estimate하고 있는 Q이기 때문에
-
장점 : state-action pair가 무한대로 존재한다면 optimal Q*로 갈 수 있음
- behavior policy에 대한 Q가 아니라 어떤 모종의 optimal policy에 대한 Q이기 때문에
- step size가 Robbins-Munro sequence 조건만 만족하고 state-action을 무한히 방문하면 optimal policy로 수렴하게 됨
- behavior policy가 epsilon greedy로 남아있더라도 상관없음
- GLIE보다 좋은 점
-
Maximization Bias
- state-action value가 unbiased하더라도 가 biased될 수 있음
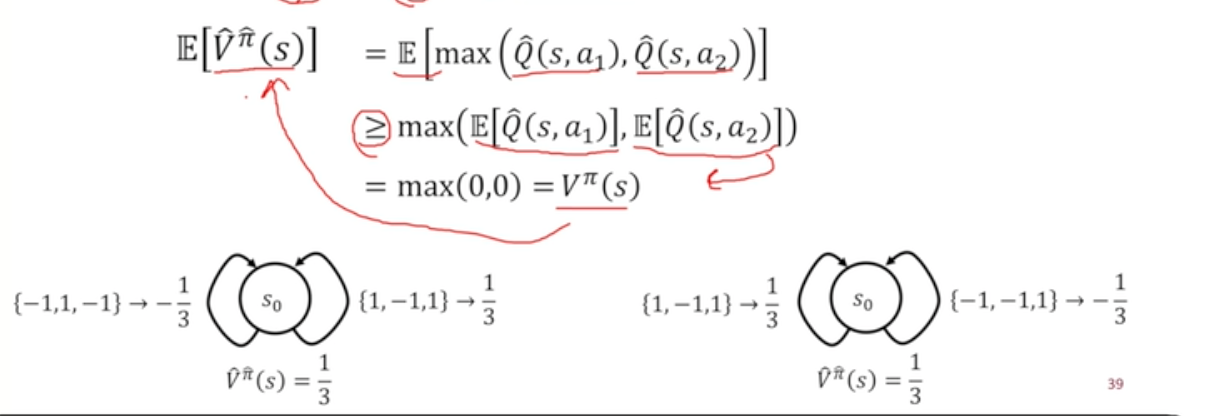
-
기댓값 취하는 과정에서 두개의 max 함수 존재
-
max를 취하기 때문에 원래의 값보다 항상 더 커질 수 있음
→ 이를 해결하기 위해 Double Q-learning 존재
-
- state-action value가 unbiased하더라도 가 biased될 수 있음
-
Double Q-learning
-
Maximizer (action을 고르는 Q-function)과 Estimator (계산한 Q-function) 두개가 correlation 되어 있어서 Maximization Bias발생
-
이 두가지를 분리하여 Q1, Q2 서로 다른 독립적인 estimate를 학습
-
action을 고를 때 Q1 활용
-
Q-learning 알고리즘에 쓰일 estimator로는 Q2
-
Q2에 대한 expectation을 취하기 ~ unbiased estimator

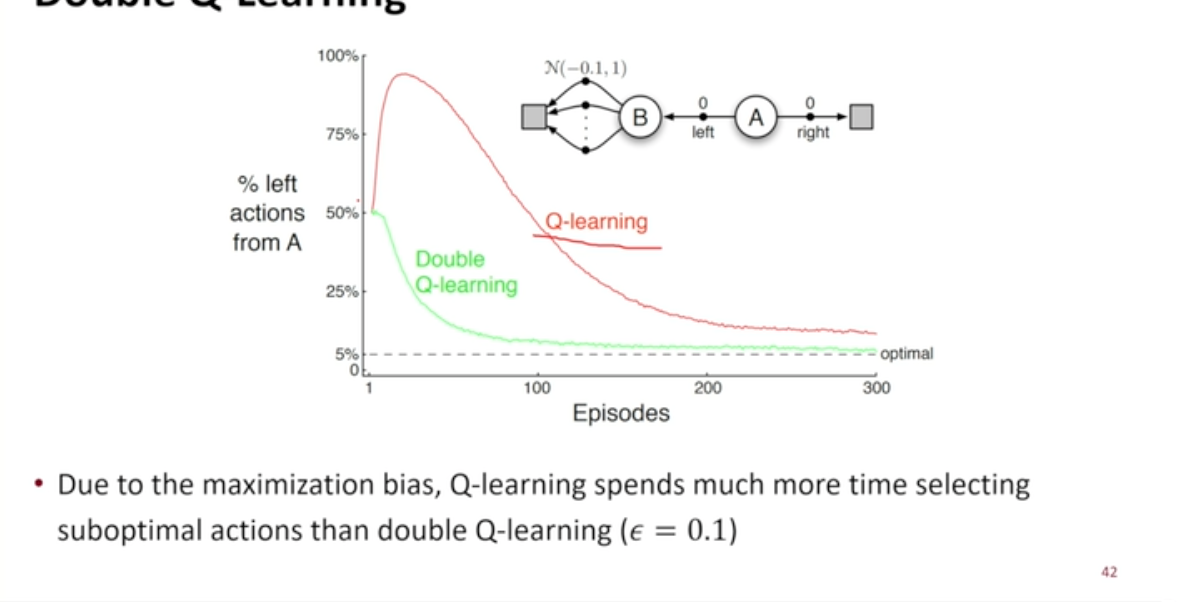
-
초반 Q-learning의 학습을 나쁘게 만드는 것 : maximization bias
-
-
-
-
-
SARSA vs Q-learning
- Example
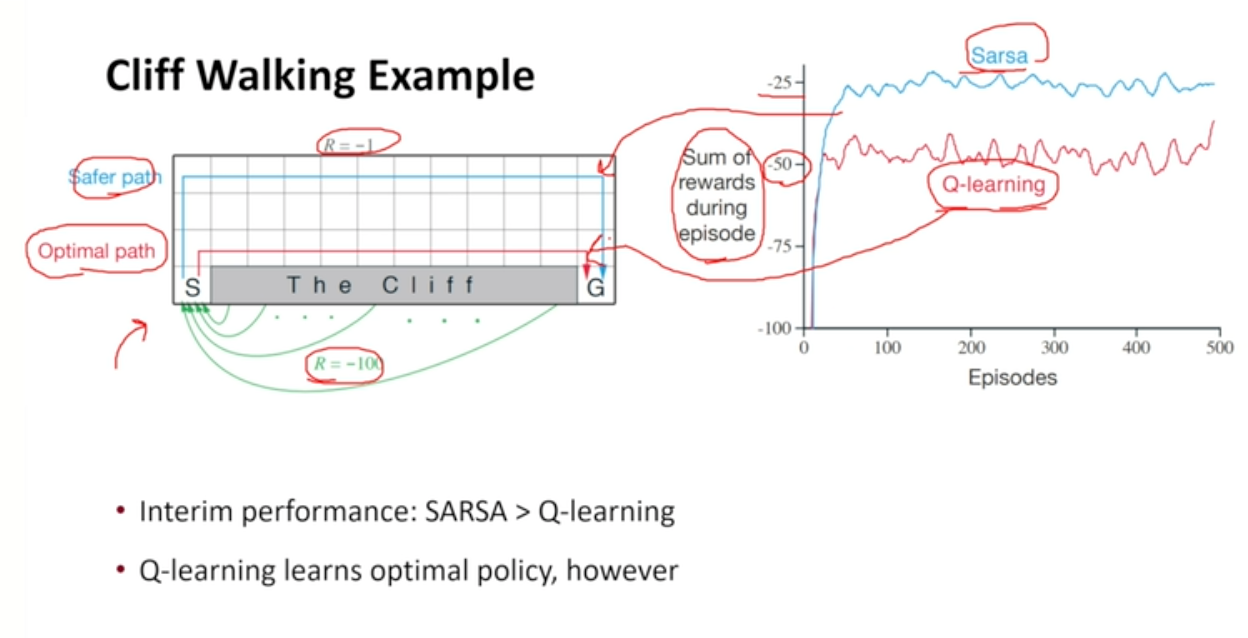
- SARSA : 매우 안전한 길 채택
- epsilon greedy를 따르더라도 행동과 보상 모두 같은 함수를 활용하므로 가장 안전한 길 채택
- Q-learning : 안전하지 않은 Optimal path 선택
- optimal path를 가다가 cliff로 떨어지게 됨
- 결과적으로 optimal path를 학습하고 있기는 함
- epsilon을 스케쥴링하지 않아도 되기 때문에 신경을 덜 써도 됨
- SARSA : 매우 안전한 길 채택
- Example
- Diagram

-
Function Approximation
- Tabular Representation 가정을 깨어 더 다양하고 어려운 문제를 해결할 수 있는 방법
- 실세계의 문제 : state-action space가 매우 크기 때문에 벡터, 매트릭스 형태의 데이터를 활용한다면 학습에 어려움 존재
- Tabular Representation 활용할 경우 Continuous State Space에 대해서 다룰 수 없음
→ 이를 해결하기 위해 Function Approximation
-
가정
- 모든 각각의 state에 대해 학습하고 싶지 않음 - 모든 state에 대해, 모든 action에 대해 학습하는 것은 매우 어려움
- 여러개의 state와 여러개의 action에 걸쳐 일반화될 수 있는 representation 상에서 학습하고자 함 → 메모리, 계산량, 데이터 양을 줄일 수 있음
-
종류
- 선형 함수
- 뉴럴 네트워크
- 이외에도 결정트리 등 다양하나 미분가능한 상태의 함수에 대해서만 배우고자 함
-
Gradient Descent
- J를 최소화하는 파라미터 w구하는 것이 목표
- w를 gradient만큼 이동시키기
-
Value Function Approximation for Policy Evaluation with Oracle
- 지도학습과 유사 ~ Oracle(State, 이 주어지기 때문에

- expectation 대신 state를 샘플링하여 update 진행
- 지도학습과 유사 ~ Oracle(State, 이 주어지기 때문에
-
Model Free VFA Policy Evaluation
- Oracle이 주어지지 않은 상황에서 어떻게 해야할 것인가
- Feature Vecture : state를 나타내기 위한 벡터 설계
- Linear Approximation :
 → update rule : step size ( feture value
→ update rule : step size ( feture value
- 가 없는 상황에서
-
MC에서는 이를 대신하여 사용
-
TD에서는 이를 대신하여 TD target 사용

-
- MC 가정 하에 : unbiased estimator ~ regression 학습 문제

- Linear Value Function Approximation을 했을 때 우리가 원하는 곳으로 향하게 되는가
- MC에서는 minimum value error를 구하는 가중치 w를 구할 수 있게 됨

- 기본적인 SGD와 동일하게 작용하기 때문에 linear에서는 optimal answer로 가게됨
- TD 가정 하에 우리가 의도한 곳으로 가는가
- Sampling + Bootstrapping + Value Function Approximation 까지 추가되었을 때 우리가 의도하는 곳으로 가는지가 중요함

- TD target이 주어져 있는 지도학습 문제로 볼 수 있음
- Update Formula : step size TD error() x(s)
- TD target으로 변환했는데 이게 우리가 원하는 gradient를 구하는 방식이 맞는가
- update formula 자체는 실제 objective에 대한 gradient라 할 수 없고 (가 TD target에도 존재하기 때문에 이에 대한 미분 값도 남아있음) gradient와 비슷한 형태의 update를 진행하기에 Semi-Gradient Update라고 불리움 (Semi-Gradient TD(0))

- update formula 자체는 실제 objective에 대한 gradient라 할 수 없고 (가 TD target에도 존재하기 때문에 이에 대한 미분 값도 남아있음) gradient와 비슷한 형태의 update를 진행하기에 Semi-Gradient Update라고 불리움 (Semi-Gradient TD(0))
- TD target으로 변환했는데 이게 우리가 원하는 gradient를 구하는 방식이 맞는가
- Semi-Gradient TD(0)

- on-policy 알고리즘에 대해서는 Semi-Gradient TD fixed point 항상 존재 (만 Robbins-Munro 컨디션에 따라 스케쥴링 한다면 로 수렴)
- 1 / (1-gamma)를 곱한 경우 좋은 경우는 아님 ~ 상한이 존재하나 꽤나 좋은 estimator라고 말하기에는 무리가 있음
- Sampling + Bootstrapping + Value Function Approximation 까지 추가되었을 때 우리가 의도하는 곳으로 가는지가 중요함
- MC에서는 minimum value error를 구하는 가중치 w를 구할 수 있게 됨
- control with Value Function Approximation

-
있다고 가정 = Oracle 존재

-
- Convergence of TD methods
- Bellman backup = contraction
- value function approximation = expansion
- 수렴 여부에 대해 증명하는 것이 쉽지 않음
- Linear Case & On-policy 에 대해서
- TD(0), SARSA(0)이 수렴하는 것 증명 가능
- Non-Linear & Off-policy에 대해서는 수렴 보장 불가능

- Function Approximation + Bootstrapping + Off-policy training = 발산 가능
-
Linear Value-function Geometry

-
True SGD TD algorithms
-
MC 알고리즘 : true SGD methods
-
TD 알고리즘 : Semi-Gradient
-
TD error를 줄이면 어떨까?

- semi-gradient TD(0)과 비교하여 마지막 항이 하나 더 생기게 됨
- 이를 residual-gradient term이라고 부름 → 이는 converge 함
- TD error를 줄이는 방향으로 감
- 이것이 과연 우리가 원하는 방향인가?
- TD error를 줄이는 것 : 를 최소화하는 것과 동일
- BUT 우리가 원하는 것 :
- ~ 분산만큼의 차이 존재 가능
- 이상한 곳에 수렴할 수도 있음
-
-
Minimizion the Bellman Error
- minimizes = minimize Bellman Error
- gradient 유도식
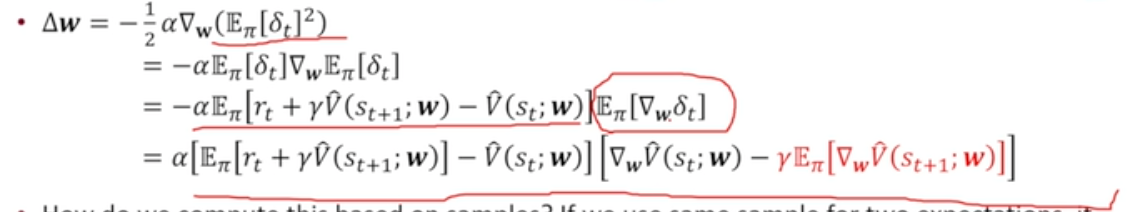
- 하나의 sample을 활용하여 2개의 기댓값 계산할 수 없음
- 이럴 경우 이전의 naive residual-gradient algorithm과 동일
- 해결 위해서는 : double sampling이라고 불리우는 next state를 가져와 서로 independent한 sample을 통해 gradient를 평가해야 함

- 하나의 state에서 다음 state 2개를 샘플링하는 것은 가능하지 않아 실제 사용되지는 않음
- 하나의 sample을 활용하여 2개의 기댓값 계산할 수 없음
-
-
Further Developments of TD algorithms
- Objective : Projected Bellman Error를 0으로 만드는 로 가는 알고리즘을 찾아야 한다.
- Semi-Gradient TD가 PBE를 0으로 만드는 지점을 찾을 수 있으나
- off-policy에서는 optimization이 diverse할 수 있는 가능성이 생김
Deep Q Learning
- Neural Network기반 Function Approximation 알고리즘
- 2014에 제안된 중요한 알고리즘 중 하나
- 기존 Linear value function approximation을 위해서는 좋은 feature(state)를 손수 찾아내야 하는 과정이 필요했으나 적절한 Neural Net을 활용할 경우 그 과정이 더이상 필요하지 않게 됨
- Deep Neural Networks
- local representation 대신 다양한 뉴런들에 의한 distributed representation으로 활용됨
- 충분히 많은 뉴런만 있으면 모든 함수를 approximate 가능 : Universal function approximator
- Shallow Network에 비유하여 Deep하게 layer를 쌓아가면 기하급수적으로 적은 수의 node, parameter를 필요로 함
- SGD를 통해 파라미터 학습
- CNN
- RL에서 많이 활용되는 알고리즘
- Fully connected network보다 훨씬 적은 수의 파라미터를 통해 효율적인 feature extraction 가능
- Value, Q-function을 neural network로 표현하기
-
지난시간 복습
- w의 update를 구할 때 oracle을 대신하는 target (TD 등)을 맞춤
- 이를 반복하여 update하면 좋은 방향으로 움직인다.
-
Deep RL in ATARI
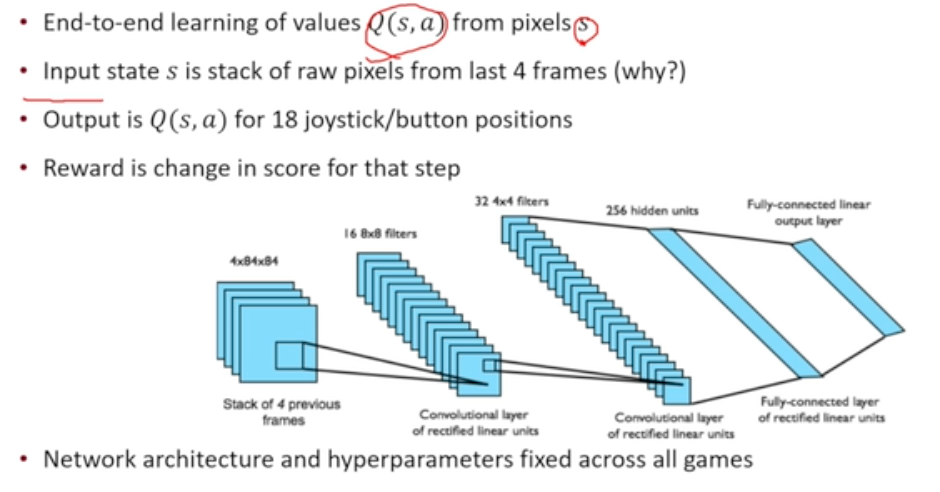
- state가 입력되어 action개수만큼 Q가 나오는 형태
- descrete, finite action에 대해서 이렇게 활용 가능
- input : 4개의 frame을 stack하여 활용
- 이때, MDP를 가정 ~ 하나의 이미지만 활용할 경우 속도, 가속도에 대한 정보 알 수 없음
- 이 정보를 알아내기 위해 4개의 frame stack하여 활용 (그렇다고 모든 정보를 반영한 것은 아님)
- 실제 완벽한 optimal policy는 아니더라도 어느정도 좋은 policy 얻어낼 수 있음
- output : joy stick의 18가지 움직임에 대한 output 얻을 수 있음
- reward : score가 그 state에서 얼마나 바뀌었는가
- 네트워크 구조, 하이퍼 파라미터가 모든 게임에 대해 fix 되어 있다!!!
-
Deep Q-learning
- 어떻게 해야 이 알고리즘을 SGD와 흡사하게 만들 수 있을 것인가
- correlation between samples
- non-stationary targets
- Value Function Approximation할 때 사용한 Q-learning
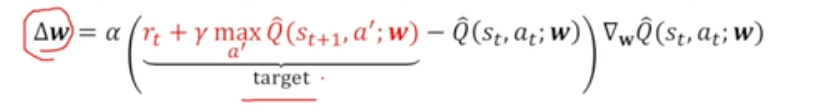
- 이것이 일반적인 SGD와 어떻게 다른가
- TD target : w에 dependent함 ~ semi-gradient rule이 더이상 SGD가 아님 → 해결 위해 target을 w에 independent하게 만들기
- 이어지는 update들 간 correlation이 크다
-
TD learning을 하게 되면 각각의 update가 서로 상관있게 된다 ~ SGD와 다른 부분
→ SGD : 모든 sample이 iid 이어야 함 (정반대의 형태)
-
- SGD처럼 행동한다면 diverse 안하게 되지 않을까?
- TD target : w에 dependent함 ~ semi-gradient rule이 더이상 SGD가 아님 → 해결 위해 target을 w에 independent하게 만들기
- 이것이 일반적인 SGD와 어떻게 다른가
- Correlation을 없애기 위해
- experience sample이 들어오면 바로 활용하지 않고 Dataset에 저장 ~ Replay buffer
- 매번 training은 기존 buffer에서 하나를 골라서 이것을 활용하여 학습 → Sample 사이의 correlation 사라짐
- Target이 non-stationary함(w에 dependent함)을 없애기 위해
- target에 있는 weight()을 다른 것으로 활용하기 (빨간 글씨 속)
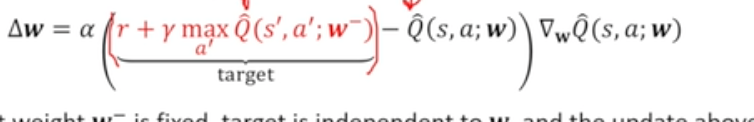
- 라는 파라미터 활용
- w- : target에서 활용되는 파라미터이지만 실제로 update하는 w와 흡사하나 완전히 동일해서는 안됨
- w- 파라미터는 update 상에서 변화하지 않도록 고정 ~ target에 대해 independent하게 됨
- 단점 : 메모리가 2배 소요됨 (파라미터 2개 활용하므로 [w, w-])
- target에 있는 weight()을 다른 것으로 활용하기 (빨간 글씨 속)
-
pseudo code
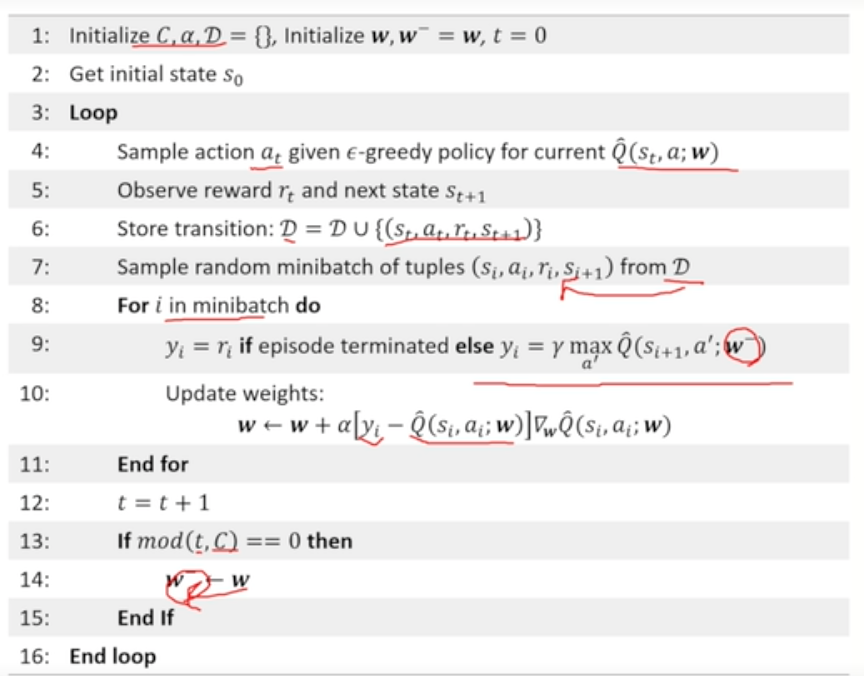
-
이외의 detail
- Huber loss
- RMSProp
- 어떻게 해야 이 알고리즘을 SGD와 흡사하게 만들 수 있을 것인가
-
- DQN의 가장 큰 성공요인
- divergence, stable learning의 문제를 해결하지 않고서는 deep neural network쓰는 것이 능사가 아님
- Stability 이슈 해결 필요
- target Q fix
- replay buffer - 가장 중요한 역할
- correlation을 줄여줌
- 데이터 재사용 가능
- 수학적으로 증명된 바는 없음
- 연구 동향
-
Double DQN
-
Double Q-learning - maximization bias challenge 해결을 위함
- Q1과 Q2 분리
-
Double Q-learning의 아이디어를 Deep Q-learning으로 확장
-
function approximator가 무거워지며 2개의 Q를 활용하는 것이 문제가 됨
-
DQN에서 활용했던 Q network를 재사용하는 것
- w- : target Q
- w : online Q ~ 우리가 update하는 Q
-
action selection에는 online Q, action evaluation에는 target Q 활용

-
별도 2개의 Q를 활용하지 않더라도 Q를 분리해낼 수 있음
-
Double DQN이 DQN보다 안정적으로 성능이 증가함
-
DQN이 발산 / over-estimation하기 시작하는 시점부터 DQN의 성능이 매우 떨어짐
- over-estimation을 막는 Double DQN이 성능 향상에 핵심적인 역할 해냄
-
-
-
Priorized Experience Replay
- Impact of Replay
- Replay buffer에서 replay를 뽑을 때,
- TD learning에서 update를 어떤 순서로 하는지가 성능에 영향 미칠 수 있음
- update가 덜 된 value에서 update를 해주면 학습 속도 빠르게 만들 수 있음
- update를 반복해줌으로써 학습 속도를 개선할 수 있지 않을까
- update tuple
- random sampling
- 순서 정해주기 ~ 기하급수적으로 학습 속도가 빨라짐
- Replay buffer에서 replay를 뽑을 때,
- Experience 뽑을 때 Priority를 DQN error(TD error)가 클수록 학습할 수 있는 여지, 더 좋아질 수 있는 여지가 많다고 판단하여 샘플링 가중치 부여
- priority에 비례하게 새로운 sample을 구함
- Impact of Replay
-
Dueling DQN
- Value & Advantage Function
-
neural architecture를 바꿔보는 법
-
value를 나타내기 위한 feature와 action 사이에 성능 차이를 나타내기 위한 feature가 서로 완전히 다를 수 있다.
-
advantage function 사용
- 어떤 action이 현재의 policy를 따라갔을 때에 비해 얼마나 advantage가 있느냐
-
V 예측 + advantage 예측
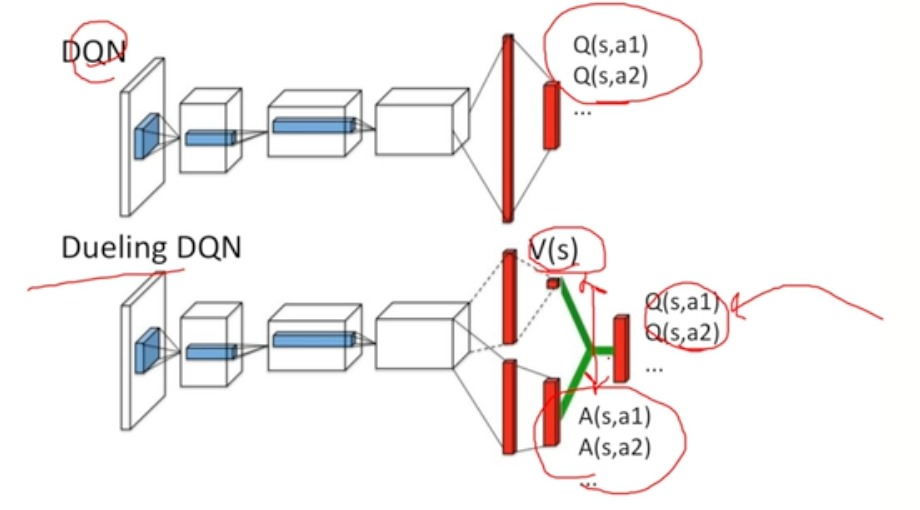
-
- Value & Advantage Function
-
Policy Gradient
- Policy based learning (이전까지는 Value based learning)
- No value function : 학습 없음
- Learnt Policy
- 장점
- better convergence properties : SGD의 꼴을 가지고 있음
- high-dimensional / continuous action space를 가질 경우 효율적임
- value based learning의 경우 implicit한 policy를 가져가야 함
- action에 대해 maximize가 불가능한 경우도 존재함
- value based learning의 경우 implicit한 policy를 가져가야 함
- Stochastic policy 학습 가능
- 단점
- local convergence : 학습이 어려운 형태에 속함 local optimum
- policy evaluation에 기반하여 policy gradient를 구하는 과정에서 : inefficient & high variance
- 필요성
- MDP가 아닌 game을 풀 때
- 가위바위보 : 나와 상대의 action이 변화할 수 있음
- MDP가 아닌 game을 풀 때
강화학습의 기초를 다지고자 했으나 너무 방대한 내용이 담겨 있어서 이해하기가 매우 어려웠다.
관련하여 아래의 글들을 더 읽어볼 예정이다.

