이분 탐색(Binary Search)
업다운 게임
이분 탐색(Binary Search)을 이해하는 가장 쉬운 예시는 업다운 게임입니다. 업다운 게임은 1부터 50사이의 숫자를 정하고, 그 숫자를 맞추는 게임입니다.
가장 적은 횟수로 정답을 맞춰야 할 때, 1부터 순차적으로 정답을 찾는다면 최악의 경우 50번이나 시도를 해야할 수도 있습니다.

그런데, 찾고자 하는 범위를 반씩 줄여가며 찾아가면 어떨까요? 25를 외쳤는데, 사회자가 정답은 25보다 크다고 하면, 25이하의 숫자는 더이상 생각할 필요는 없습니다.
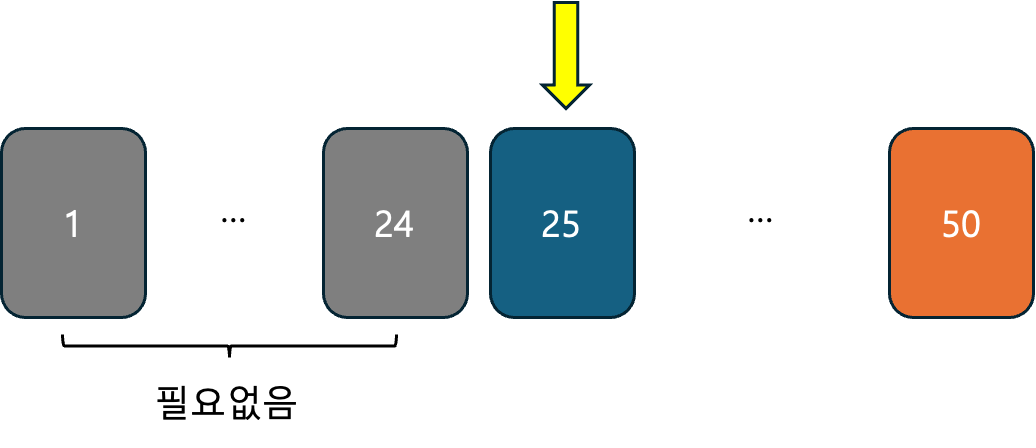
이 방법은 최악의 경우라도, 번만에 정답을 찾을 수 있습니다. 이보다 빠른 방법이 있을까요?
사실 찍어서 한 번만에 맞추면 가장 빠를 수 있습니다. 하지만 최악의 경우, 마찬가지로 50번을 찍어야 할 수도 있죠. 따라서 업다운 게임의 필승법은, 범위를 반씩 좁혀가며 찾는 방법이 가장 합리적인 방법입니다.
이렇게 범위를 반씩 좁혀가며 대상(target)을 찾는 알고리즘을 이분 탐색(Binary Search)라고 합니다.
앞선 예시처럼 단순히 어떤 정수를 찾는게 아니라, 자료를 뒤져서 특정 값이 존재하는지 찾는 경우에는, 해당 자료가 정렬되어 있어야 합니다. 그래야 대소 비교를 통해 절반의 범위를 확실히 날릴 수 있기 때문입니다.
설명과 코드

위와 같이 정렬된 배열이 있습니다. 여기서 50을 이분 탐색을 이용해 찾는 방법은 다음과 같습니다.

처음에 찾는 범위는 배열 전체입니다. 따라서 범위의 왼쪽 끝 left은 인덱스로 0, 오른쪽 끝 right은 배열 길이-1입니다. 범위의 중심 mid은 (left + right) / 2입니다.
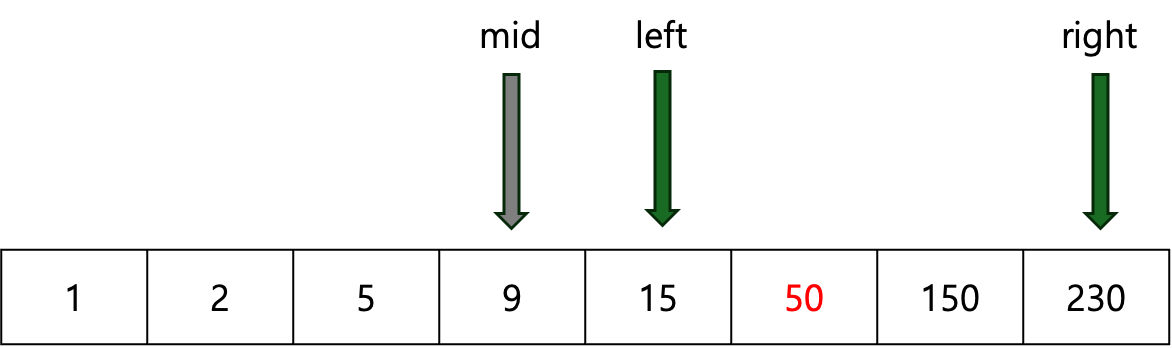
mid의 값이 target보다 작으므로, 범위는 mid의 오른쪽으로 좁혀져야 합니다. 따라서 left는 mid+1로 업데이트 되어야 합니다.

새로운 범위에서 똑같은 방법을 반복하면, 50을 2번만에 찾을 수 있습니다.
그런데, 배열에서 50이 없었다면 어떻게 될까요?

여기서 target은 57보다 작으므로, 범위는 mid의 왼쪽으로 좁혀져야 합니다. 따라서 right는 mid-1로 업데이트 되어야 합니다.

똑같이 반복하면, mid의 값이 target보다 작으므로, 범위는 mid의 오른쪽으로 좁혀져야 합니다. 따라서 left는 mid+1로 업데이트 되어야 합니다.


이때, left가 right보다 커지는 역전이 발생하였습니다. 이는 배열에서 찾고자 하는 target이 없음을 뜻하고, while문은 종료됩니다.
코드는 다음과 같습니다.
#include <iostream>
#include <vector>
using namespace std;
vector<int> arr = { 1,2,5,9,15,50,150,230 };
int binarySearch(int target);
int main()
{
int tmp = binarySearch(50);
if (tmp == -1)
cout << "존재하지 않음\n";
else
cout << "index = " << tmp << '\n';
return 0;
}
int binarySearch(int target)
{
int left = 0;
int right = arr.size() - 1;
while (left <= right)
{
int mid = (left + right) / 2;
// 정답을 찾았으면 해당 인덱스 리턴
if (target == arr[mid])
return mid;
// target이 mid값보다 크다면, 탐색 범위는 오른쪽
if (target > arr[mid])
left = mid + 1;
// target이 mid값보다 작다면, 탐색 범위는 왼쪽
else
right = mid - 1;
}
return -1; // 없으면 -1 리턴
}lower bound
- lower bound는 목표보다 크거나 같은 값이 최초로 나오는 위치를 말합니다
- 이분 탐색을 이용하여 lower bound를 구현할 수 있습니다

lower bound 구현
다음 배열에서 20의 lower bound를 구해봅시다.

20보다 크거나 같은 원소들을 True로 표시할 때, 결국 첫 번째 True가 나오는 위치를 찾는 것입니다. 이때,
- True인 곳의 오른쪽은 항상 True가 나온다
- True인 곳의 왼쪽은 True가 나올 가능성이 있다
- False인 곳의 오른쪽은 True가 나올 가능성이 있다
이런 규칙을 봤을 때, 다음과 같이 범위를 좁혀나가야 합니다.
mid가 True이면 왼쪽을 탐색한다mid가 False이면 오른쪽을 탐색한다
upper bound
- upper bound는 목표보다 큰 값이 최초로 나오는 위치를 말합니다.
- 이분 탐색을 이용하여 upper bound를 구현할 수 있습니다.
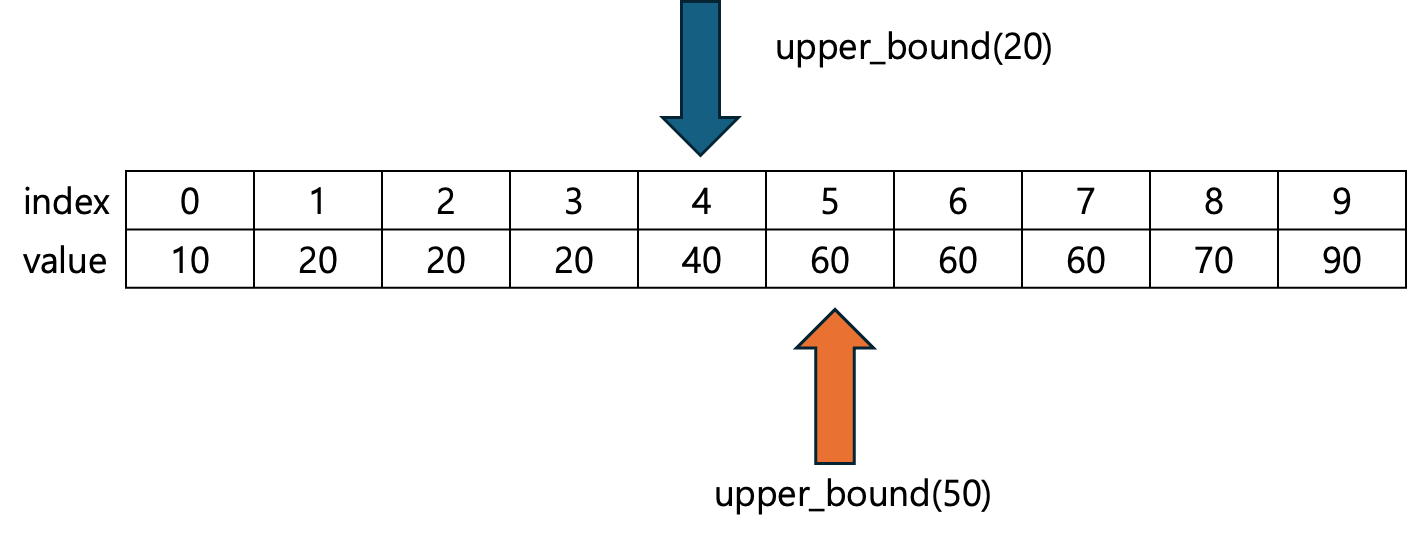
upper bound 구현
다음 배열에서 20의 upper bound를 구해봅시다.
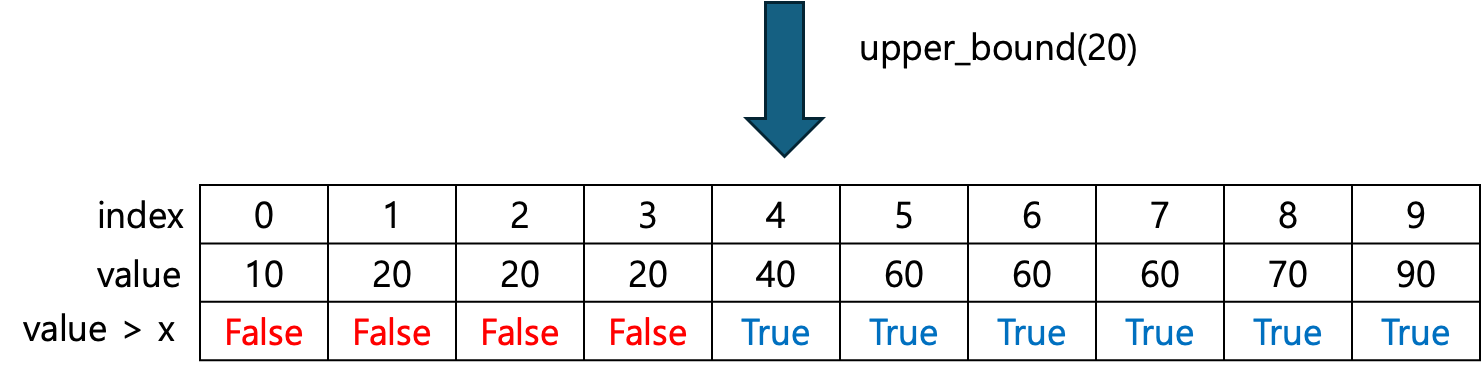
20보다 큰 원소들을 True로 표시할 때,
- True인 곳의 오른쪽은 항상 True가 나온다
- True인 곳의 왼쪽은 True가 나올 가능성이 있다
- False인 곳의 오른쪽은 True가 나올 가능성이 있다
이런 규칙을 봤을 때, 다음과 같이 범위를 좁혀나가야 합니다.
mid가 True이면 왼쪽을 탐색한다mid가 False이면 오른쪽을 탐색한다
즉, 로직상으로 lower bound와 동일합니다. 다만 구현 시 조건 차이가 있을 뿐입니다.
파라매트릭 서치(Parametric Search)
공장에서 작업 속도 조정 문제
공장에서 제품을 하루에 100개 생산해야 한다고 가정해봅시다. 기계의 속도를 조정해 이 목표를 달성하려고 할 때, 어떻게 해결할 수 있을까요?
첫 번째로, 기계의 속도와 작업 시간을 계산하여 한 시간에 몇 개의 제품을 생산해야 하루 100개를 정확히 생산할 수 있는지 계산합니다. 예를 들어, 한 시간에 10개를 생산할 수 있는 속도로 10시간을 일하면 100개를 정확히 생산할 수 있다는 계산이 나옵니다.
하지만 현실에서는 기계 성능, 오작동, 생산 변동 등 다양한 요소를 정확히 반영하기 어려워 계산만으로는 이상적이지 않을 수 있습니다.
두 번째는 목표를 "기계 속도를 조정해 하루에 100개 이상 생산할 수 있는 최소 속도를 찾아라"라는 결정문제로 변환합니다. 이 경우, 기계 속도를 먼저 대략적으로 설정하고 테스트를 진행합니다.
- 하루 100개를 생산하기에 속도가 너무 느리면 기계 속도를 조금 올려보고,
- 너무 빨라서 오버프로덕션이 발생하면 속도를 줄입니다. 이렇게 속도가 적절한지 아닌지(yes or no)를 반복적으로 확인하면서 이분탐색으로 답을 좁혀갑니다.
두 번째 방법과 같이 문제를 "결정문제"로 변형하고, 답을 좁혀가는 이분탐색을 활용하는 것을 파라매트릭 서치라고 합니다.
자동차 연료 게이지 문제
문제
10개의 글자로 이루어진 한 문자열이 있습니다.
- "#######___"
#은 기름을 나타낸다._은 빈 칸을 나타낸다.
기름이 총 몇 칸이 채워져 있는지를 찾는 문제입니다.
설명
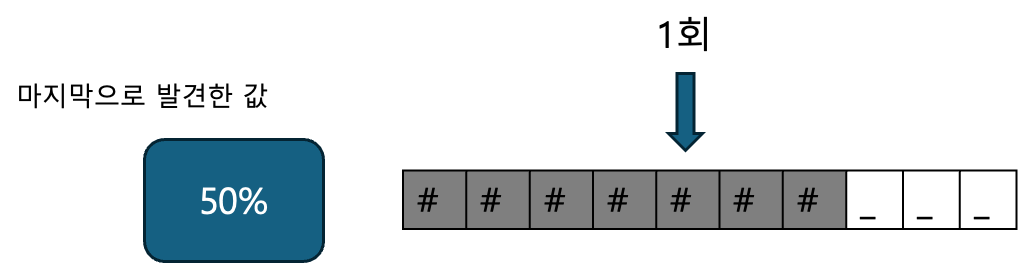
파라매트릭 서치로 해당 문제를 해결해봅시다. 먼저 가운데(5번째)를 한 번 살펴봅니다. 가운데는 #이므로, 이보다 많은 기름이 차있는 걸 예상할 수 있습니다.

다음은 미지의 영역의 중간(8번째)을 살펴봅니다. 이곳은 빈칸이므로, 최댓값이 존재하는 영역은 현재 위치에서 왼쪽입니다.
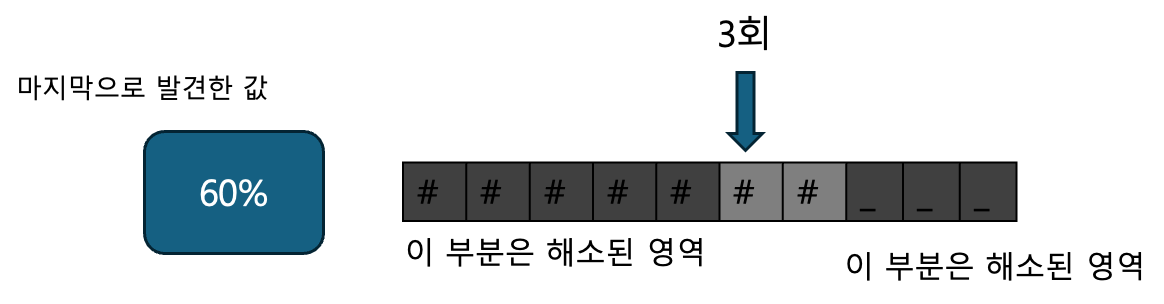
기름칸이므로 최댓값을 갱신하고, 오른쪽 영역을 더 살펴봅니다.

마찬가지로 기름칸이므로 최댓값을 갱신하고, 오른쪽 영역을 더 살펴봅니다.

더이상 살펴볼 영역이 없으므로, 최댓값은 70%이고, 이 값이 정답이 됩니다.
소스코드
위 과정을 그대로 소스 코드로 작성하면 다음과 같습니다.
#include <iostream>
#include <string>
using namespace std;
string gauge = "#######___";
bool test(int mid);
int parametricSearch();
int main()
{
cout << parametricSearch() << '\n';
return 0;
}
bool test(int mid)
{
if (gauge[mid] == '#') return true;
else return false;
}
int parametricSearch()
{
int left = 0;
int right = gauge.size() - 1;
int mid, rst = 0;
while (left <= right)
{
mid = (left + right) / 2;
if (test(mid))
{
rst = mid; // 최댓값 갱신
left = mid + 1; // 오른쪽 영역 검사
}
else
right = mid - 1;// 왼쪽 영역 검사
}
return mid + 1; // 인덱스니까 +1
}츄러스 나눠먹기 문제
문제

현재 길이가 50cm, 30cm, 40cm인 츄러스 3개가 있습니다.
총 다섯 명의 사람이 츄러스를 정확히 똑같은 사이즈로 잘라 한 덩어리씩 나눠먹으려고 합니다. 최대 몇 cm로 나누어먹을 수 있을까요?
설명
이 문제는 이미 지문에서 파라매트릭 서치를 암시하고 있습니다. 5명이 최대 몇 cm로 나누어먹을 수 있는지는 "공장 작업 속도 조정 문제"와 별 차이가 없기 때문입니다.
- 대충 여기 잘라볼까 -> 어 아니네 or 어 충분하네 -> 덜 잘라 or 더 잘라 -> 대충 여기 잘라볼까...
Try1 : 1 ~ 50
처음에 가능한 범위는 1cm ~ 50cm입니다. 여기서 절반인 25cm가 가능한지 확인(yes or no)합니다.

- 츄러스 1(50cm) -> 25cm 2개
- 츄러스 2(30cm) -> 25cm 1개
- 츄러스 3(40cm) -> 25cm 1개
4개를 만들 수 있으므로, 5명에게 나눠줄 수 없습니다. 따라서 자르는 길이를 줄여야 합니다.
-> 정답이 될 수 있는 범위 : 1cm ~ 24cm
Try2 : 1 ~ 24
다시 정답이 될 수 있는 범위에서 절반인 13cm가 가능한지 확인합니다.

- 츄러스 1(50cm) -> 13cm 3개
- 츄러스 2(30cm) -> 13cm 2개
- 츄러스 3(40cm) -> 13cm 2개
7개를 만들 수 있으므로, 5명에게 나눠줄 수 있습니다. 따라서 자르는 길이를 늘려도 됩니다.
- 정답이 될 수 있는 범위 : 14cm ~ 24cm
Try3 : 14 ~ 24
다시 절반인 19cm가 가능한지 확인합니다.

- 츄러스 1(50cm) -> 19cm 2개
- 츄러스 2(30cm) -> 19cm 1개
- 츄러스 3(40cm) -> 19cm 2개
5개를 만들 수 있으므로, 5명에게 나눠줄 수 있습니다. 따라서 자르는 길이를 늘려도 됩니다.
- 정답이 될 수 있는 범위 : 19cm ~ 24cm
...
이렇게 반복했을 때, 더 이상 범위를 줄일 수 없는 지점에 도달하게 됩니다. 이때 마지막으로 가능했던 길이가 바로 정답이 됩니다. 그리고 그 정답은 20cm입니다.
소스코드
위 설명을 코드로 작성하면 다음과 같습니다.
#include <iostream>
#include <vector>
using namespace std;
vector<int> chu = { 50, 30, 40 };
bool test(int mid);
int parametricSearch();
int main()
{
cout << parametricSearch() << '\n';
return 0;
}
bool test(int mid)
{
int sum = 0;
for (int i = 0; i < chu.size(); i++)
sum += chu[i] / mid;
if (sum >= 5)
return true;
else
return false;
}
int parametricSearch()
{
int left = 1;
int right = 50;
int rst, mid = 0;
while (left <= right)
{
mid = (left + right) / 2;
if (test(mid))
{
rst = mid;
left = mid + 1;
}
else
right = mid - 1;
}
return mid;
}