[자료구조 및 알고리즘] Sort1 (C++)

신동욱·2025년 5월 9일

자료구조 및 알고리즘

목록 보기

8/18

🎯 Sorting이란?

정렬(Sorting)은 특정 기준에 따라 데이터의 순서를 재배열하는 과정입니다.

입력: 임의의 순서로 나열된 원소 집합
기준: 오름차순(작→큰) 또는 내림차순(큰→작)을 결정하는 비교 함수
출력: 기준에 맞춰 순서대로 정렬된 원소 집합

정렬은 다양한 알고리즘에서 핵심 전처리 단계로 활용됩니다.

예시: 숫자를 오름차순으로 정렬하면…

이진 탐색을 사용해 $𝑂(log⁡𝑛)$ 시간에 원하는 값을 빠르게 찾을 수 있습니다.🔍

📈 정렬 알고리즘의 복잡도

정렬 알고리즘은 주로 비교(Comparisons)와 교환(Exchanges) 횟수로 복잡도를 분석합니다.

비교(Comparisons): 두 아이템의 순서를 결정
교환(Exchanges): 실제로 두 아이템의 위치를 바꿈

🛠 주요 정렬 알고리즘

1. Bubble Sort 🫧

개념: 인접한 두 요소를 비교하고, 큰 값을 뒤로 보낸다.
동작:
1. 인접한 두 개를 비교
2. 앞이 더 크면 교환
3. Pass가 한 번 끝나면 가장 큰 값이 맨 뒤에 위치
복잡도: 비교 횟수 = $\sum_{k=1}^{n-1} k = O(n^2)$

for (int pass = 0; pass < n-1; pass++) {
    for (int i = 0; i < n-1-pass; i++) {
        if (A[i] > A[i+1]) swap(A[i], A[i+1]);
    }
}

2. Selection Sort 🔍

개념:
- bubble sort보다 교환을 덜 하는 방식
- 매 Pass마다 가장 작은(또는 큰) 요소를 선택해 제자리에 둠.
동작:
1. 전체에서 최소값(index minIdx) 찾기
2. minIdx와 현재 기준 위치 i를 교환
복잡도: $O(n^2)$ 비교, $O(n)$ 교환

for (int i = 0; i < n-1; i++) {
    int minIdx = i;
    for (int j = i+1; j < n; j++) if (A[j] < A[minIdx]) minIdx = j;
    swap(A[i], A[minIdx]);
}

3. Insertion Sort 🧩

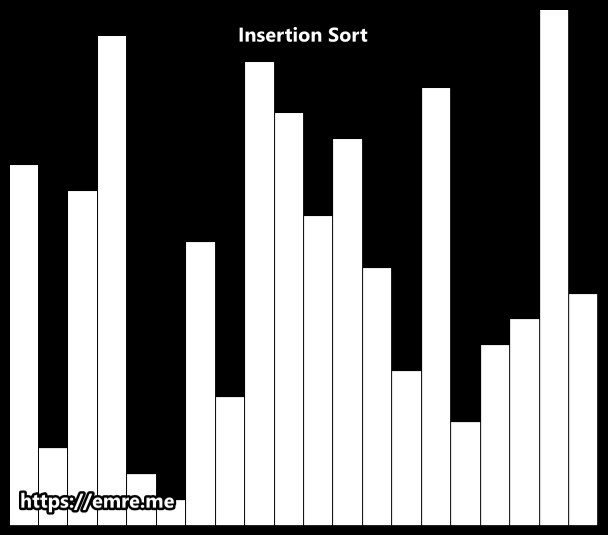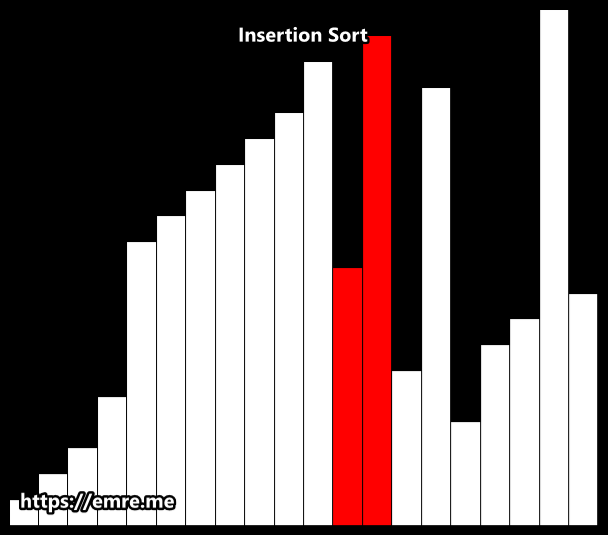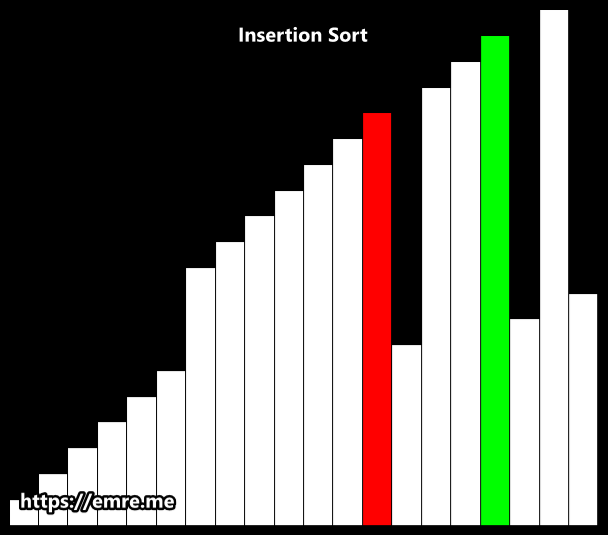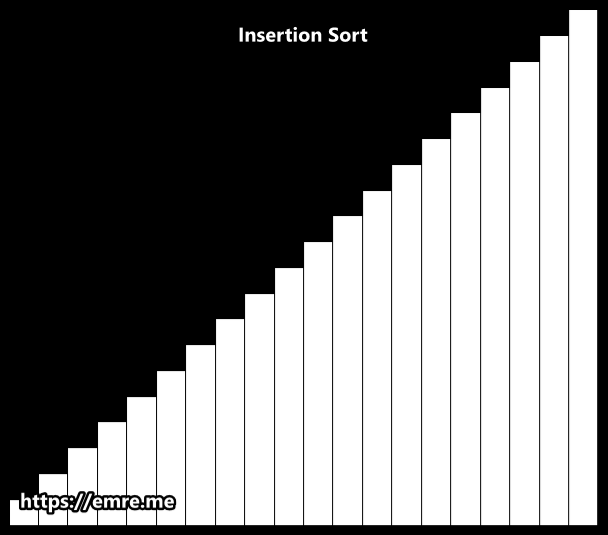
개념:
- 이미 정렬된 부분(sublist)에 새 요소를 삽입하며 확장
- 정렬되어 있으면, 내 위치를 찾았을 때 더 이상 탐색하지 않아도 됨
동작:
1. A[0..i-1]이 정렬되어 있다고 가정
2. A[i]를 적절한 위치로 집어넣기
복잡도: 평균/최악 $O(n^2)$ , 최선 $O(n)$

for (int i = 1; i < n; i++) {
	int tmp = v[i];
	int j = i;
	// 나보다 작은 애 만날 때까지 앞으로 전진
	while (j >= 1 && v[j-1] > tmp) {
		swap(v[j], v[j - 1]);
		j--;
	}
}

4. Shell Sort 🐚

개념:
- 한계: Insertion Sort는 역순일 때 $O(n^2)$
- Shell의 아이디어: 간격(gap)만큼 떨어진 요소들끼리 먼저 정렬 → 전체가 거의 정렬된 상태가 되어 최종 삽입 정렬이 빨라짐.
동작:
1. 초기 gap = n/2, gap > 0일 때마다 gap /= 2
2. 각 gap마다 i = gap..n-1에 대해 삽입 정렬 수행
복잡도: Gap 시퀀스에 따라 다르나, 일반적으로 $O(n^{1.5})$

void shellsort(vector<int>& A) {
	int n = A.size();
	// gap 시퀀스
	for (int gap = n/2; gap > 0; gap /= 2) {
		// 각 시퀀스의 두 번째 요소부터 끝까지 돌기
		for (int i = gap; i < n; i++) {
			int temp = A[i];
			int j = i;
			// 나보다 작은 애 만날 때까지 앞으로 전진
			while (j >= gap && A[j - gap] > temp) {
				swap(A[j], A[j - gap]);
				j -= gap;
			}
		}
	}
}

5. Merge Sort 🌉

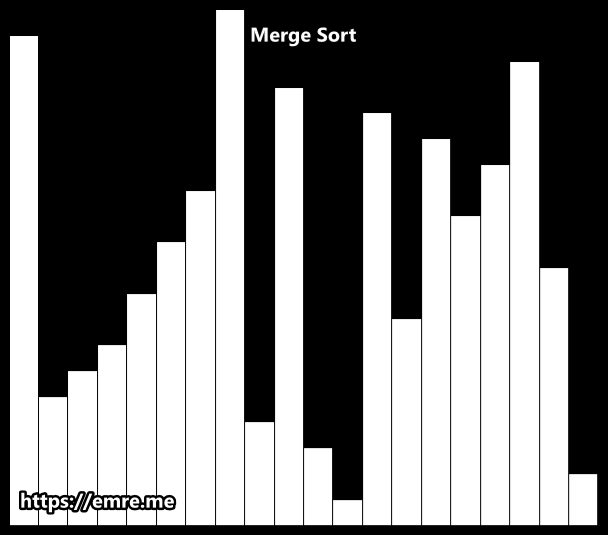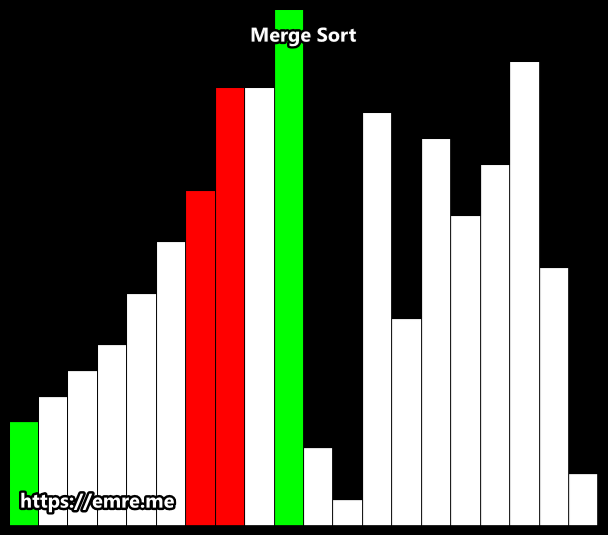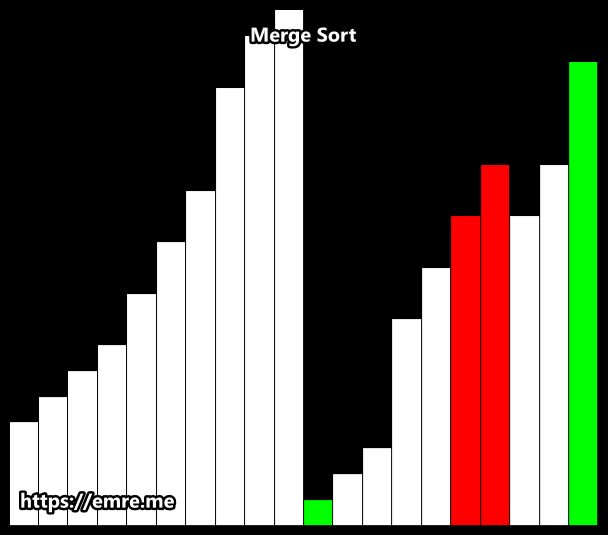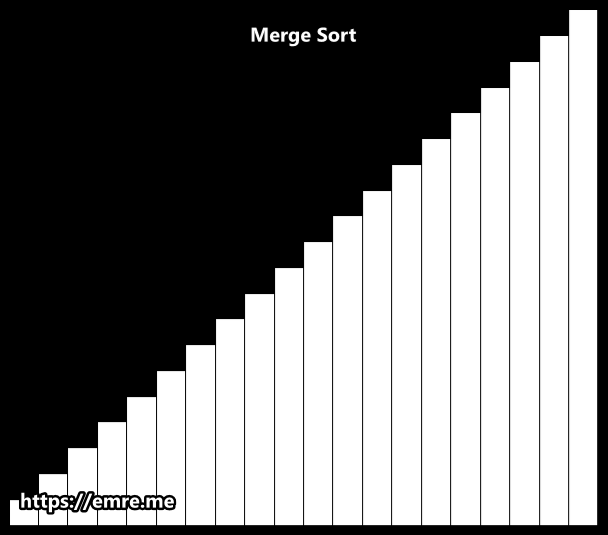
개념: 분할 정복(Divide & Conquer)
동작:
1. 리스트를 반으로 계속 나눔
2. 길이 1이 되면 멈추고, 합칠 때 정렬하며 병합

병합(Merge):

다음 두 정렬된 서브리스트를 병합한다고 해봅시다.

왼쪽 서브리스트 $L = [2, 5, 7, 9]$
오른쪽 서브리스트 $R = [1,3,8]$

병합 과정은 다음과 같이 진행됩니다.

단계	비교 대상	작은 값 선택	tmp 배열 상태	L 포인터(i)	R 포인터(j)
1	$L[i]=2$ vs $R[j]=1$	1 (R[j])	[1]	i=0	j=1
2	$L[i]=2$ vs $R[j]=3$	2 (L[i])	[1, 2]	i=1	j=1
3	$L[i]=5$ vs $R[j]=3$	3 (R[j])	[1, 2, 3]	i=1	j=2
4	$L[i]=5$ vs $R[j]=8$	5 (L[i])	[1, 2, 3, 5]	i=2	j=2
5	$L[i]=7$ vs $R[j]=8$	7 (L[i])	[1, 2, 3, 5, 7]	i=3	j=2
6	$L[i]=9$ vs $R[j]=8$	8 (R[j])	[1, 2, 3, 5, 7, 8]	i=3	j=3 (끝)
---	R 소진	—	[1, 2, 3, 5, 7, 8]	i=3	j=3
7	남은 L 붙이기	9 (L[i])	[1, 2, 3, 5, 7, 8, 9]	i=4 (끝)	j=3

최종 병합 결과:

[1, 2, 3, 5, 7, 8, 9]

복잡도: 깊이 log n × 각 레벨 O(n) = $O(n log n)$

void merge_sort(vector<int>& A, int l, int r) {
    if (l >= r) return;
    int m = (l + r) / 2;
    merge_sort(A, l, m);
    merge_sort(A, m+1, r);
	
    // 병합
    vector<int> tmp;
    int i = l, j = m+1;
    while (i <= m && j <= r) {
        if (A[i] <= A[j]) tmp.push_back(A[i++]);
        else tmp.push_back(A[j++]);
    }
    // 남은 원소 처리
    while (i <= m) tmp.push_back(A[i++]);
    while (j <= r) tmp.push_back(A[j++]);
	// 다시 원본 배열에 복사
    for (int k = l; k <= r; k++) A[k] = tmp[k-l];
}