
🚀 더 빠른 정렬
1. Quick Sort ⚡
-
개념:
- Divide and conquer strategy
- merge sort와 비교해서 추가적인 메모리가 필요하지 않다
- pivot을 사용해서 두 개의 아이템을 비교
-
동작:
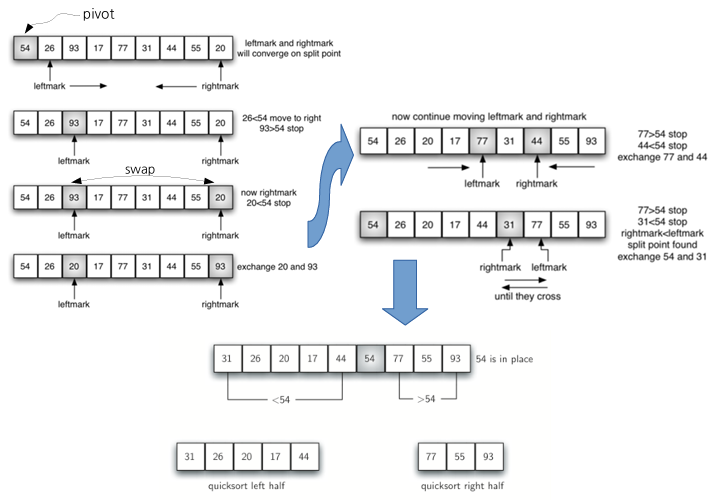
- 왼쪽에서 오른쪽으로 가면서 pivot보다 큰 아이템을 찾는다 (left mark)
- 오른쪽에서 왼쪽으로 가면서 pivot보다 작은 아이팀을 찾는다 (right mark)
- left mark와 right mark를 교환한다
- left mark와 right mark가 교차할 때까지 1-3을 반복한다
- pivot이 왼쪽 끝에 있을 때, pivot과 right mark를 교환한다 혹은 pivot이 오른쪽 끝에 있을 때, pivot과 left mark를 교환한다
- pivot에 의해 분리된 sub list들에서 4-5를 반복한다
-
복잡도:
- 평균적인 경우 : 분할이 리스트 중앙에서 일어날 때
- 최악의 경우 : 분할이 리스트 끝에서 일어날 때
void QuickSort(vector<int>& v, int l, int r) {
if (l >= r) return;
// 왼쪽으로 가면서 pivot보다 큰 아이템을 찾는다
int pivot = v[l];
int left_mark = l + 1;
int right_mark = r;
while (1) {
while (left_mark <= right_mark && pivot >= v[left_mark]) left_mark++;
while (right_mark >= left_mark && pivot <= v[right_mark]) right_mark--;
if (left_mark > right_mark) break;
swap(v[left_mark], v[right_mark]);
}
// pivot과 right mark를 교환
swap(v[l], v[right_mark]);
// divide
QuickSort(v, l, right_mark - 1);
QuickSort(v, right_mark + 1, r);
}2. Heap Sort 🌳
-
개념:
- max-heap을 이용해 매번 최댓값을 빠르게 찾고 꺼내는 정렬
- Selection Sort의 향상된 버전이라고 생각해도 됨
- Selection Sort는 으로 매번 최댓값 획득
- max-heap은 으로 가능
-
동작:
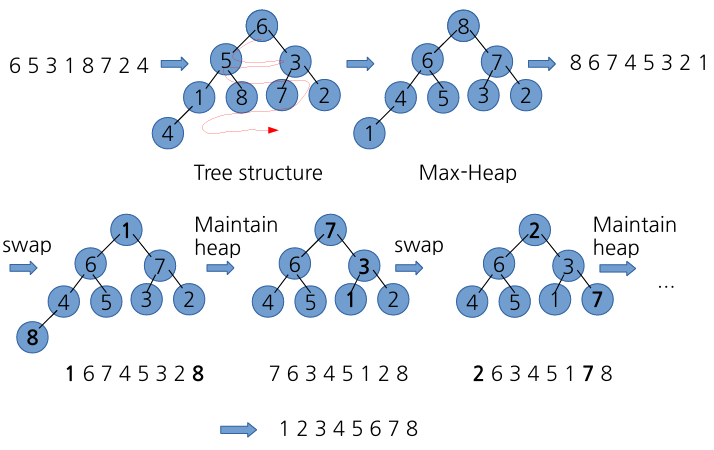
- 배열 전체를 max-heap으로 변환
- 루트(최댓값) <-> 마지막 원소 교환
- 힙 크기를 줄이고, 루트에 대해 heapify로 힙 속성 복원
- 남은 원소에 2-3 반복
-
시간복잡도 :
void heapSort(vector<int>& arr) {
int n = arr.size();
// Build max-heap : 마지막 부모 노드(n/2-1)부터 루트(0)까지
for (int i = n / 2 - 1; i >= 0; i--) {
heapify(arr, n, i);
}
// 정렬
for (int end = n - 1; end > 0; end--) {
swap(arr[end], arr[0]);
heapify(arr, end, 0);
}
}
// arr[0..n-1] 구간에서, 루트 i를 최대 힙 속성으로 재조정
void heapify(vector<int>& arr, int n, int i) {
int largest = i;
int left = 2 * i + 1; // 왼쪽 자식
int right = 2 * i + 2; // 오른쪽 자식
if (left < n && arr[left] > arr[largest]) {
largest = left;
}
if (right < n && arr[right] > arr[largest]) {
largest = right;
}
if (largest != i) {
swap(arr[i], arr[largest]);
heapify(arr, n, largest);
}
}3. Bin Sort 🗑️

-
개념:
- 입력값의 범위를 일정 빈(bin)으로 나눠 분산시키는 분할 정복과 유사한 방법
- 각 빈에 들어간 원소들은 해당 구간 내에서만 정렬
-
동작:
- 적당한 크기의 빈을 만든다
- 각 원소를 적절한 빈으로 분산
- 각 빈 안의 원소들을 삽입 정렬, 퀵 정렬 등으로 개별 정렬
- 모든 빈을 순서대로 합쳐 최종 정렬된 리스트를 만듦
-
시간 복잡도:
void binSort(float arr[], int n) {
vector<vector<float>> b(n);
for (int i = 0; i < n; i++) {
int bi = n * arr[i]; // index in bin
b[bi].push_back(arr[i]);
}
for (int i = 0; i < n; i++) {
sort(b[i]);
}
int index = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < b[i].size(); j++) {
arr[index++] = b[i][j];
}
}
}4. Radix Sort 🔢
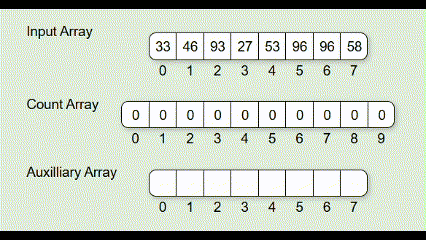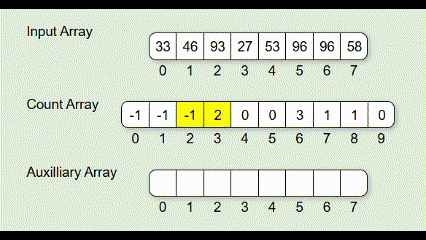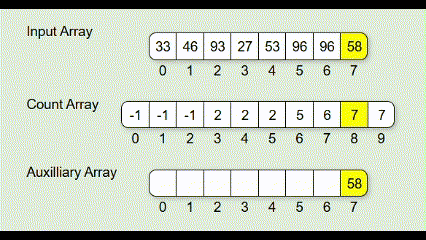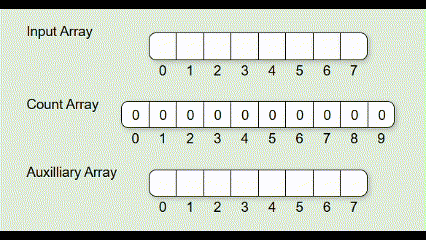
-
개념:
- 정수의 자리수(digit)을 기준으로 반복적으로 분배하고 취합하여 정렬하는 방식
- 자리수는 최하위 자리(LSD)부터 최상위 자리(MSD)로 처리
-
동작 (index array method):
- 입력 값 중 최댓값의 자리수
d를 구함 exp=1부터 시작해서exp*=10씩 증가시켜 가면서, 모든 값의(value/exp)%10자리수를 기준으로 안정 정렬exp가 이상이 될 때까지 2 반복
- 입력 값 중 최댓값의 자리수
-
시간복잡도:
void radixSort(vector<int>& arr) {
int mx = arr[0];
// 1) 최댓값 찾기
for (int& v : arr) {
if (v > mx) mx = v;
}
// 2) exp = 1, 10, 100 , ... 처리 == 첫 번째 자리 -> 마지막 자리
for (int exp = 1; mx / exp > 0; exp*=10) {
countSortByDigit(arr, exp);
}
}
void countSortByDigit(vector<int>& arr, int exp) {
int n = arr.size();
vector<int> output(n);
int count[10] = { 0, };
// 1) 해당 자리수별 빈도 계산
for (int i = 0; i < n; i++) {
int digit = (arr[i] / exp) % 10;
count[digit]++;
}
// 2) 누적합으로 위치 계산
count[0] = -1; // for 0-based index
for (int i = 1; i < 10; i++) {
count[i] += count[i - 1];
}
// 3) 뒤에서부터 위치 찾기
for (int i = n - 1; i >= 0; i--) {
int digit = (arr[i] / exp) % 10;
output[count[digit]] = arr[i];
count[digit]--;
}
// 4) 원래 배열에 복사
for (int i = 0; i < n; i++) {
arr[i] = output[i];
}
}정렬 알고리즘 비교
| Sorting method | algorithm | complexity | stability |
|---|---|---|---|
| Bubble Sort | Exchanging two neighbor items | stable | |
| Selection Sort | Finding the maximum of the remained items | stable | |
| Insertion Sort | Keeping the previous list sorted | stable | |
| Shell Sort | Sorting sub-lists by gab | ~ | stable |
| Merge Sort | Splitting list and merging sub-lists recursively (additional memory) | stable | |
| Quick Sort | Splitting list according to pivot value and swapping recursively | Avg.: Worst case: | unstable |
| Heap Sort | Utilizing max-heap (additional memory | unstable | |
| Bin (bucket) Sort | Hashing by MSB and sorting each bin (additional memory) | stable | |
| Radix Sort | Hashing from LSB to MSB (additional memory) | stable |
Stable vs Unstable Algorithms
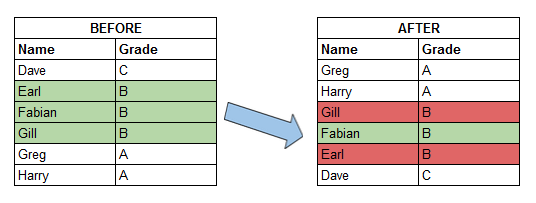
- stable : 정렬 시 같은 값을 갖는 아이템들의 순서가 유지됨
- unstable: 그렇지 않음
