[자료구조 및 알고리즘] Tree (C++)

🌳 Tree Data Structure

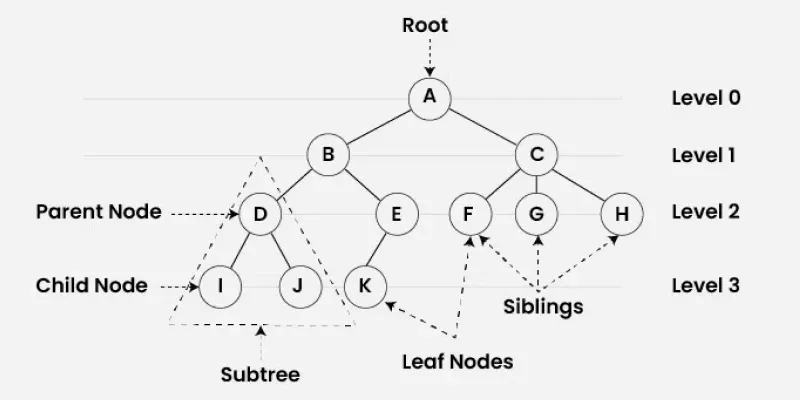
Tree는 비선형 구조로 원소들 간에 1:n 관계를 가지는 자료구조입니다. 상위 원소에서 하위 원소로 내려가면서 확장되는 트리(나무)모양의 구조이기 때문에, Tree라고 합니다.

• 개념:

  • 계층적(hierarchical) 구조를 가지며, 최상위의 하나의 루트(root) 노드에서 시작해 여러 갈래(branch)를 거쳐 리프(leaf) 노드들로 뻗어 나가는 구조

  • 루트를 제외한 모든 노드는 정확히 하나의 부모(parent) 노드로부터 오는 단 하나의 들어오는 간선(incoming edge)를 갖는다 (단방향)

  • 루트에서 각 노드까지의 경로(path)는 유일하며, 이는 트리의 계층적 특성을 보장

• 정의:
  한 개 이상의 노드로 이루어진 유한 집합이며, 다음 조건을 만족합니다.

  1. 노드 중 최상위 노드를 루트(root)라 한다.
  2. 나머지 노드들은 n(n>=0)개의 분리 집합 T1, ..., TN으로 분리될 수 있다.
  3. 이들 T1, ..., TN 은 각각 하나의 트리가 되며(재귀적 정의) 루트의 부 트리(subtree)라 한다.

• 기본 용어 및 표기:

  단어	뜻
  노드(node)	트리를 구성하는 기본 단위로, 일반적으로 값을 나타내는 키(key)를 가짐
  엣지(edge)	두 노드를 연결하는 선(간선)
  루트(root)	부모가 없는 최상위 노드
  부모(parent)·자식(children)	어떤 노드 A에서 뻗어나간 엣지로 연결된 노드 B가 있을 때, A를 부모, B를 자식이라 함
  형제(sibling)	같은 부모를 공유하는 노드들
  경로(path)	여러 노드가 차례로 연결된 순서
  부분트리(subtree)	트리 내의 어떤 노드와 그 아래로 뻗어 있는 모든 노드들로 이루어진 작은 트리
  레벨(level)	루트가 0레벨, 그 자식들은 1레벨, ...과 같이 각 노드의 깊이를 나타냄
  높이(height)	루트에서 가장 먼 리프 노드까지의 레벨

이진 트리(Binary Tree)

• 개념:
  • 트리의 각 노드가 최대 두 개의 자식만 갖도록 제한한 것을 이진트리라고 함
  • 이진 트리는 구현과 탐색 알고리즘이 단순해, 다양한 응용에 폭넓게 사용됨
• 트리 순회(Tree Traversal):
  

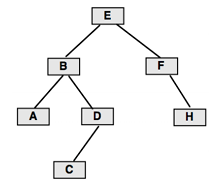
순회(Traversal)란, Tree의 각 노드를 중복되지 않게 전부 방문하는 것을 말합니다.

• Breadth first traversal:
  • 같은 레벨을 먼저 순회
  • E > B > F > A > D > H > C
• Depth first traversal:
  • 최대한 깊게 순회
  • Preorder(전위): root > left child > right child
    • E > B > A > D > C > F > H
  • Inorder(중위): left child > root > right child
    • A > B > C > D > E > F > H
  • Postorder(후위): left child > right child > root
    • A > C > D > B > H > F > E

---

Priority Queues with Binary Heaps

핵심 개념

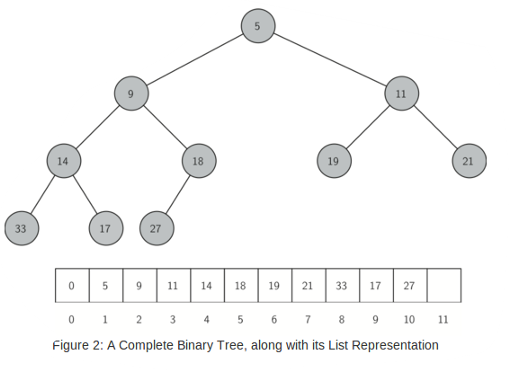
• 완전 이진 트리(Complete Binary Tree):

  • 마지막 레벨을 제외한 모든 레벨이 꽉 차 있고, 마지막 레벨의 노드들은 왼쪽부터 채워짐
  • 배열(리스트) 하나로 표현 가능
    • 부모 인덱스 i
    • 왼쪽 자식 2*i
    • 오른쪽 자식 2*i+1
    • (1-based indexing 기준)

• 힙 속성(Heap Order Property):

  • A가 B의 부모노드이면, A의 키값과 B의 키값 사이에는 항상 일정한 대소관계가 성립하는 것

  • 키값의 대소관계는 오로지 부모노드와 자식노드 간에만 성립하며, 형제노드 사이에서는 일정한 대소관계가 정해지지 않음

  • 최소 힙(min-heap): 부모의 키 <= 자식의 키

  • 최대 힙(max-heap): 부모의 키 >= 자식의 키

Binary Heap ADT

• 데이터(Data):

  변수	설명
  currentSize	힙의 현재 크기
  heapList	아이템을 저장할 리스트

• 기능(Operators):

  연산	설명	시간 복잡도
  isEmpty()	힙이 비어 있는지 검사	$O(1)$
  size()	요소(노드) 개수 반환	$O(1)$
  insert(key)	새 키 삽입 후 up-heap 수행	$O(log n)$
  deleteMin()	루트 삭제 후 down-heap 수행	$O(log n)$
  buildHeap(a)	1-based 배열로 변환 후 각 내부 노드 down-heap	$O(n)$

Priority Queue Implementation

• isEmpty():

  bool isEmpty() { return currentSize == 0; }

• size():

  int size() { return currentSize; }

• insert(key):
  

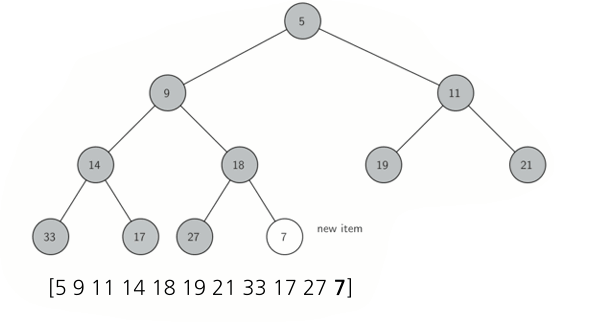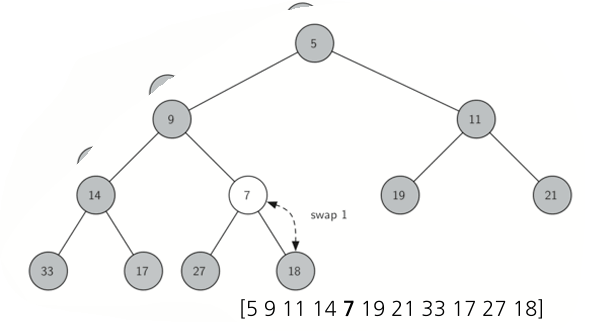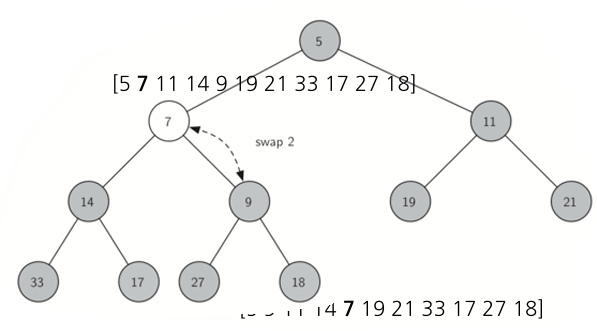
  	//새 키 삽입 후 up-heap 수행
  	bool insert(int key) { heapArray[++currentSize] = key; upHeap(currentSize); return true; }
  
  	void upHeap(size_t idx) {
  		while (idx > 1) {
  			size_t parent = idx / 2;
  			if (heapArray[parent] < heapArray[idx]) swap(heapArray[parent], heapArray[idx]);
  			else break;
  			idx = parent;
  		}
  	}

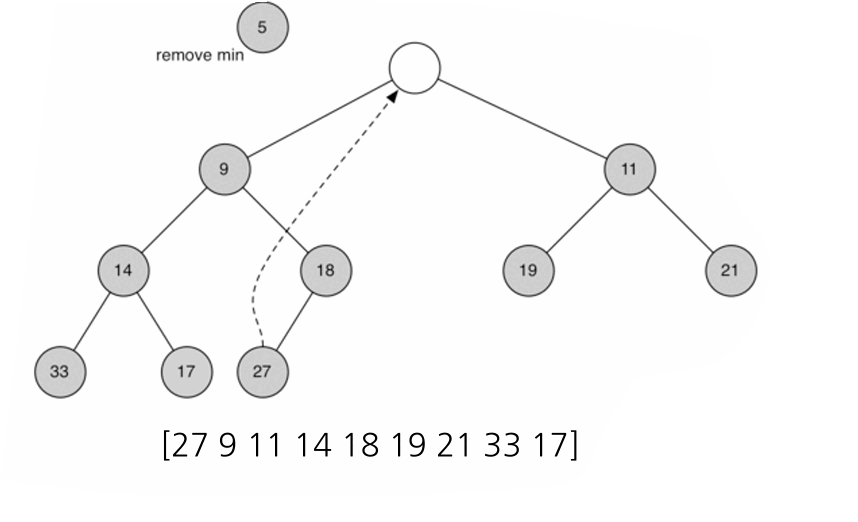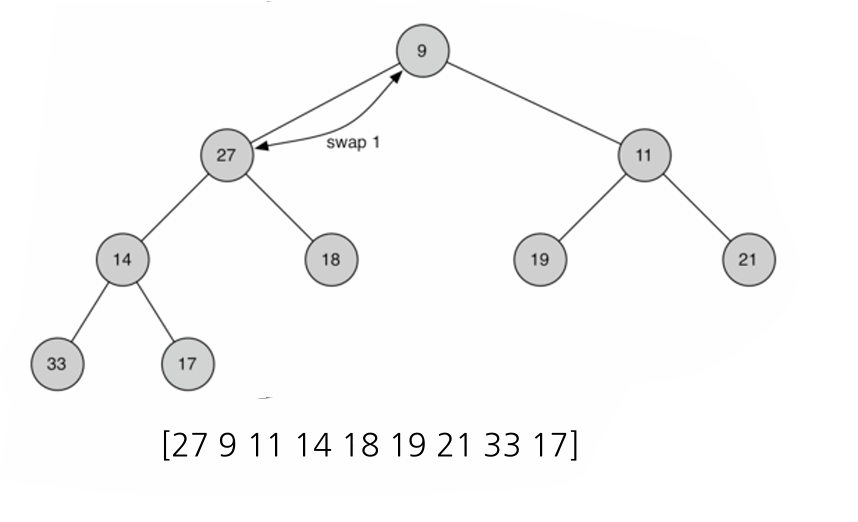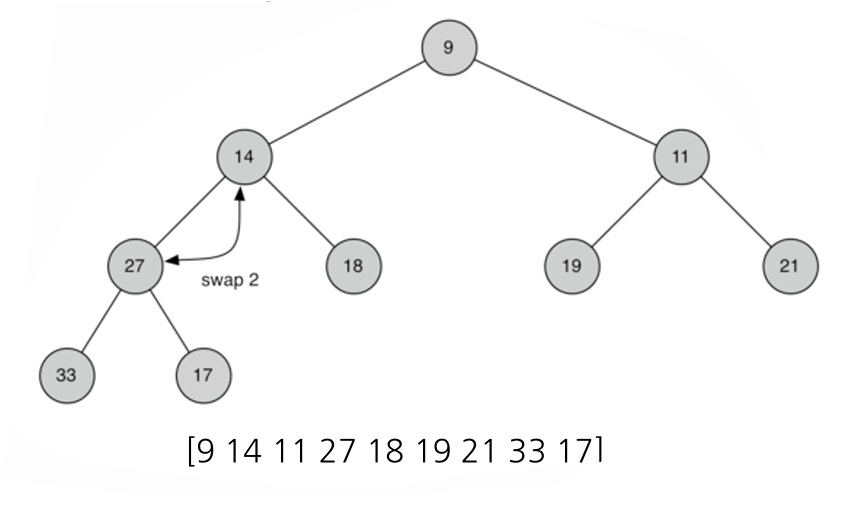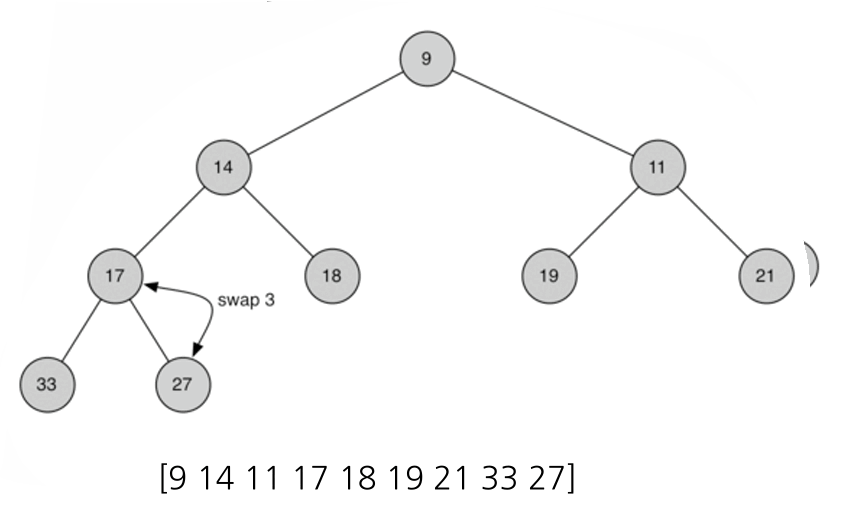
  • delMin():
    

    int delMin() {
      int retval = heapList[1];
      heapList[1] = heapList[currentSize];
      currentSize--;
      heapList.pop_back();
      downHeap(1);
      return retval;
    }
      void downHeap(int i) {
        while (i * 2 <= currentSize) {
            int mc = minChild(i);
            if (heapList[i] > heapList[mc]) swap(heapList[i], heapList[mc]);
            i = mc;
        }
    }

• buildHeap(a):
  

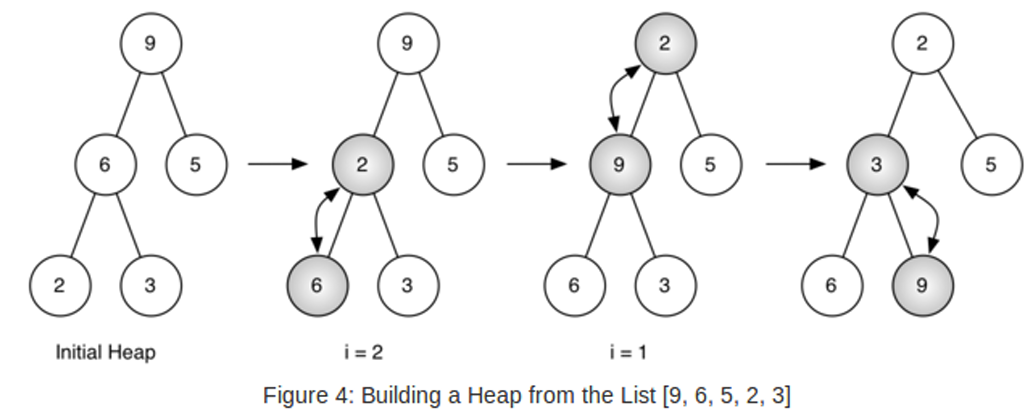
    bool buildHeap(vector<int>& alist) {
      currentSize = alist.size();
      alist.insert(alist.begin(), 0);
      heapList = alist;
      // 마지막 부모 노드(n/2)부터 루트(1)까지
      for (int i = alist.size() / 2; i > 0; i--) {
          downHeap(i);
      }
      return true;
  }

(참고) max-heap 구현

class MaxHeap {
	static constexpr size_t MAX_N = 100000; //힙 최대 사이즈 설정

	size_t currentSize = 0;
	int heapArray[MAX_N + 1] = { 0, };

	void swap(int& a, int& b) { int tmp = a; a = b; b = tmp; }

	void upHeap(size_t idx) {
		while (idx > 1) {
			size_t parent = idx / 2;
			if (heapArray[parent] < heapArray[idx]) swap(heapArray[parent], heapArray[idx]);
			else break;
			idx = parent;
		}
	}

	void downHeap() {
		size_t parent = 1;

		size_t large = parent;

		size_t left = parent * 2;
		size_t right = parent * 2 + 1;

		while (1) {
			if (left <= currentSize && heapArray[left] > heapArray[large]) large = left;

			if (right <= currentSize && heapArray[right] > heapArray[large]) large = right;
			
			//현재가 가장 크면 더 이상 down-heap을 하지 않음
			if (large == parent) break;
			else {
				swap(heapArray[parent], heapArray[large]);

				parent = large;
				
				left = large * 2;
				right = large * 2 + 1;
			}
		}
	}

public:
	MaxHeap() { memset(heapArray, 0, sizeof(heapArray)); }

	//힙 사이즈 리턴
	size_t size() { return currentSize; }

	//새 키 삽입 후 up-heap 수행
	bool insert(int key) { heapArray[++currentSize] = key; upHeap(currentSize); return true; }

	//루트값 리턴(최댓값)
	int top() { assert(currentSize != 0);  return heapArray[1]; };

	//루트값 삭제 후 down-heap 수행
	bool pop() { assert(currentSize != 0);  heapArray[1] = heapArray[currentSize--]; downHeap(); return true; }
};

출처

• 전공 강의
• GFG