FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness

Sonny020402·2023년 7월 21일

목록 보기

4/4

Introduction

Transformer는 sequence length에 quadratic하게 model size가 결정된다. 즉, self-attention의 memory complexity가 $L^2$ 라는 얘기이다. (L은 아래 그림 참조)

Model size of transformer block

이러한 문제에 대응하기 위해 approximate attention mechanism(sparse approx, low-rank approx..etc)에 대한 연구들이 진행되고 있지만, model qaulity를 포기해야만 하고 심지어 wall-clock speedup을 이루지 못하는 경우도 많다. (Think of Ahmdal’s law! IO-bound task는 FLOP을 줄인다고 크게 나아지지 않을걸?)

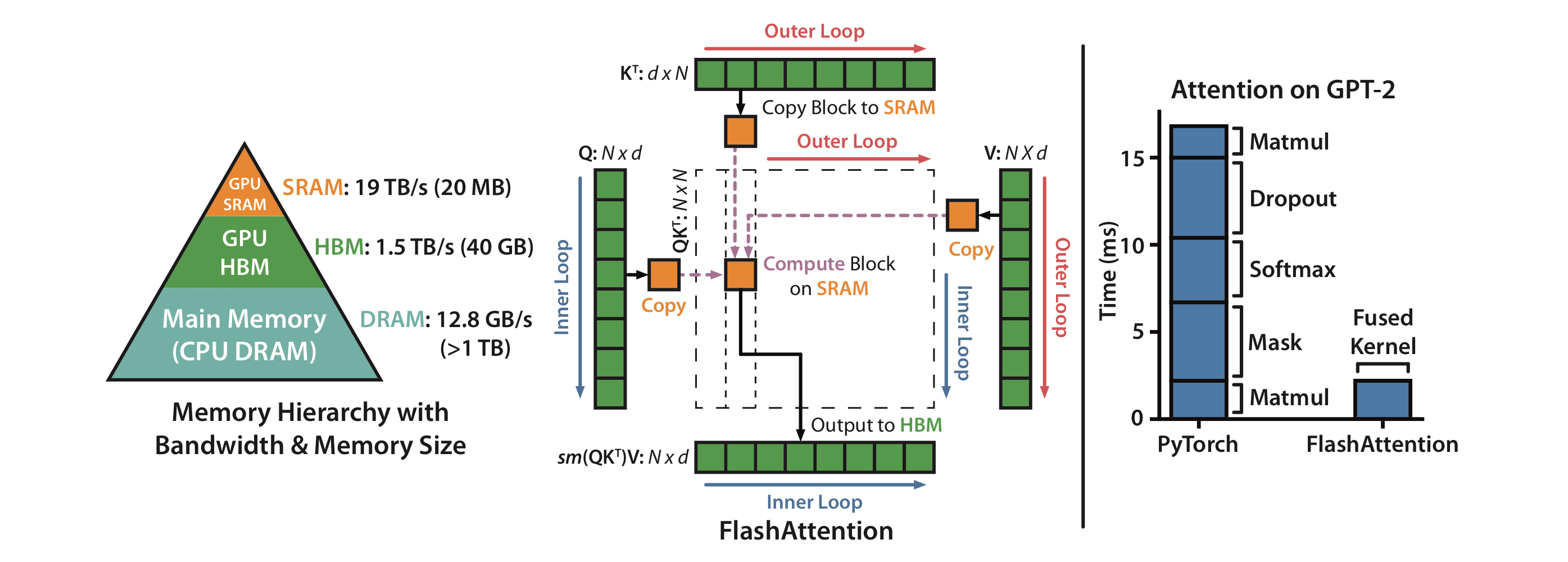
본 논문에서 제안하는 FLASHAttention은 IO-aware exact attention algorithm으로, tiling기법을 이용해(matmul에서 아주 자주 사용되는) GPU HBM의 read/write transaction을 줄인다.

Background

Hardware Performance

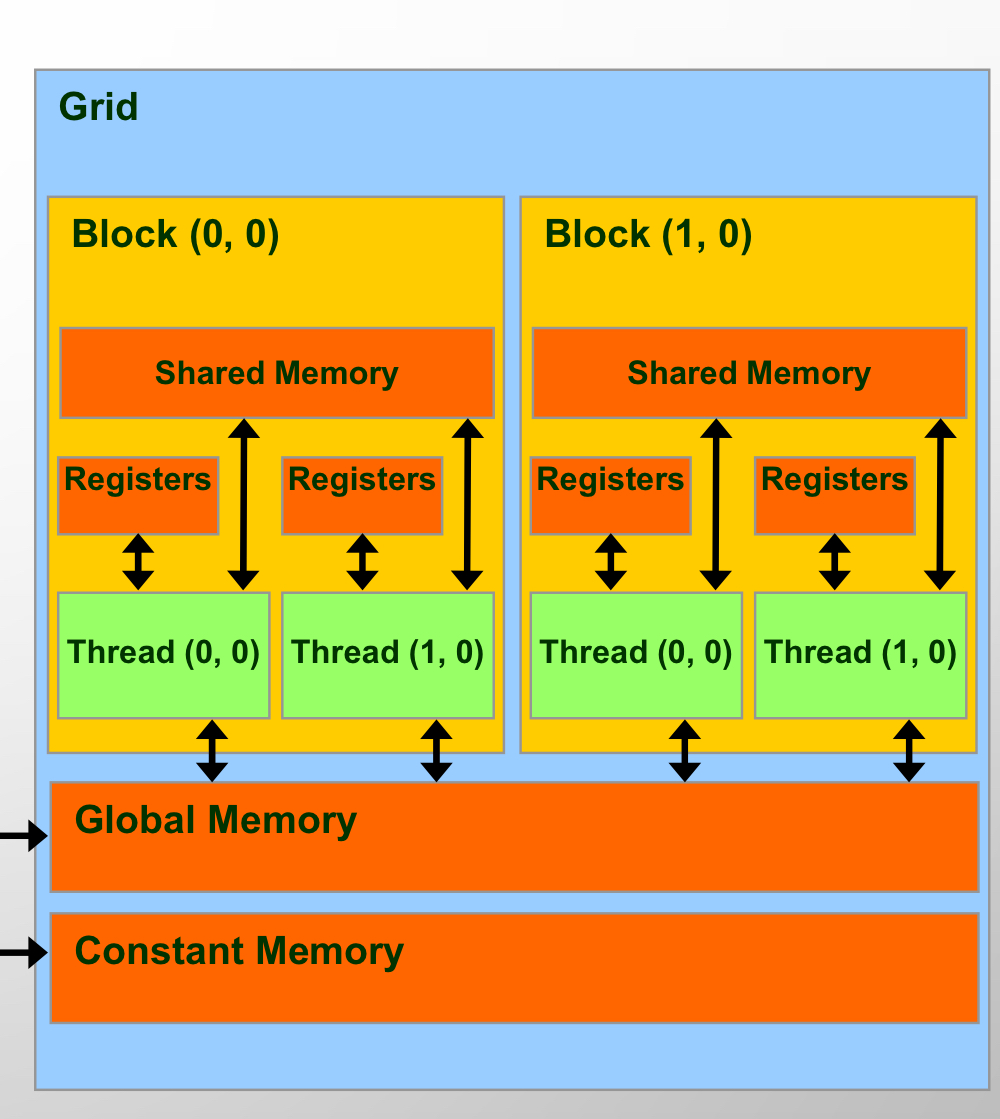
GPU memory hierarchy를 나타낸 그림이다. 각 Streaming Multiprocessor내부에 on-chip SRAM, 모든 SM에서 접근 가능한 gobal memory로 on-chip SRAM에 비해 낮은 BW를 가지는 HBM으로 구현된다. 특히나 memory bound인 attention module과 같은 경우엔, memory bottleneck을 방지하기 위해 on-chip SRAM을 잘 exploit하는 것이 매우 중요하다. (아래 그림은 systolic array에 대한 얘기지만, 상황과 잘 들어맞는 그림이당)

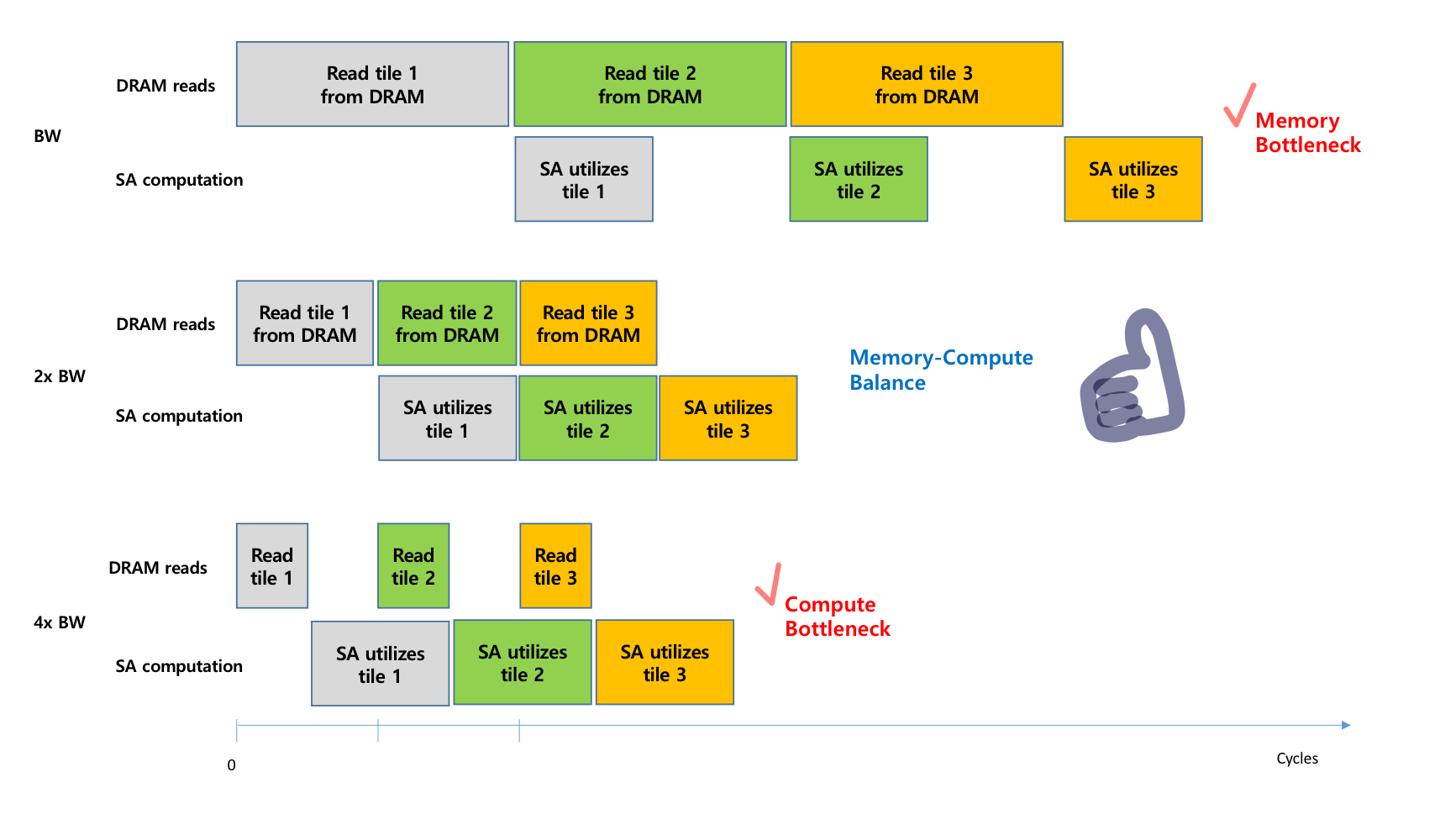
Performance characteristics: 계속 언급되고 있는 memory-bound, compute bound를 나누는 기준은 무엇일까? 바로 arithmetic intensity이다. 이는 #of arithmetic op/byte of memory access 정도로 정의할 수 있다. 이 값을 기준으로,

compute-bound == HBM에 접근하는 시간에 비해 전체 operation의 시간을 얼마나 많은 arithmetic operation이 있는지가 결정함. e.g. matrix multiplication, convolution with large # of channels

memory-bound == 전체 operation의 시간이 #of memory access에 의해 결정된다. computation을 하며 보내는 시간은 적음. e.g. elementwise ops(activation, dropout), reduction(sum, softmax, batchnorm, layernorm)

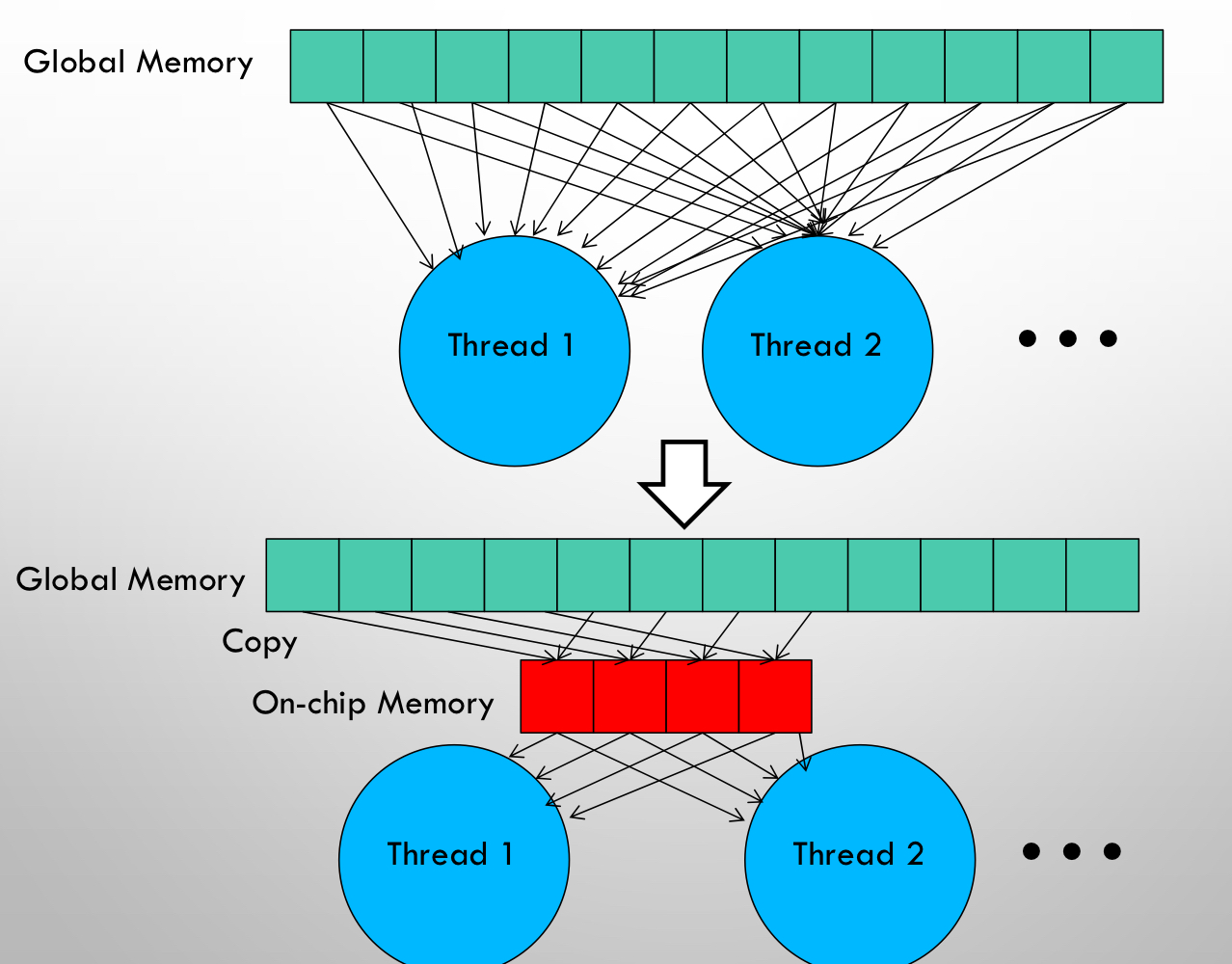
Kernel fusion: memory bound task를 가속하기 위한 가장 널리 사용되는 방법이다. 같은 입력에 대해 multiple operation을 적용하는 경우, HBM에서 해당 값을 한번만 load한 이후 여러 번 재활용하는 것이다.

compiler에서 optimization scheme으로 다양한 elementwise operation에 대해 자동으로 지원하는 경우도 있다. 그러나, model training의 관점에서 backward pass를 위해 intermediate value를 요구하기 때문에 HBM에 값을 써주는 경우가 필요하다. 즉, 일반적인 kernel fusion을 사용하는데 제약이 발생한다.

Standard Attention Implemenation

S = QK^T \in \mathbb{R}^{N\times N},\; P=softmax(S),\;O=PV\in \mathbb{R}^{N\times d}

위 softmax의 경우 row-wise 적용이라는 것을 유의하자.

FLASHATTENTION: Algorithm, Analysis, and Extensions

An efficient attention algorithm with tiling and recomputation: Query, Key, Value matrix가 주어졌을 때, self-attention output matrix인 O를 얻기까지 어떻게 N에 대해 sub-quadratic하게 HBM access를 줄일 수 있는지 알아보자. 여기서 tiling과 recomputation method를 사용한다. 그 말은, Q,K,V matrices를 block으로 쪼개어 이 단위로 fast SRAM에 loading 한 뒤, 각 블락에 대한 attention output을 만든다. 이렇게 만들어진 output matices에 대해 적절한 normalization factorfh 스케일하여 더해주면 exact attention이 계산되는 것이다.

Tiling: softmax가 어떻게 연산되는지 알아보자.

m(x) := max_i \;x_i, \; f(x):=[e^{x_1-m(x)} \;...\;e^{x_B-m(x)}], \; \\ l(x):=\Sigma_if(x)_i,\; softmax(x):={f(x)\over l(x)}

그런데 만약 vector 2개 $x^{(1)}, x^{(2)}$ concat된 $x =[x^{(1)}, x^{(2)}]$ 에 대해 softmax를 적용하고 싶다면 다음과 같이 decomposed된 manner로 계산할 수 있다.

m(x) =m([x^{(1)} , x^{(2)}])=max(m(x^{(1)}),m(x^{(2)})),\; \\f(x)=[e^{m(x^{(1)})-m(x)}f(x^{(1)}) \; e^{m(x^{(2)})-m(x)}f(x^{(2)}) \\l(x) =l([x^{(1)}, x^{(2)}]) =e^{m(x^{(1)})-m(x)}l(x^{(1)})+e^{m(x^{(2)})-m(x)}l(x^{(2)}) \\softmax(x) = {f(x)\over l(x)}

위의 equation에 의해 Q,K,V matrices를 block단위로 쪼갠 뒤 softmax를 적용하고, 다시 합칠 수 있다는 것이 보장된다. (단, 이후 combine을 위해선 extra statistics m(x), l(x)를 keep track하고 있어야 한다.)

Recomputation: Backward pass에선, QKV의 gradient를 구하기 위해 intermediate value S, P를 저장하고 있어야 한다. $O(N^2)$ 의 memory cost를 추가로 요구. 그러나, 우리(난 아님ㅋㅋ)는 이 cost를 줄이기 위한 방법을 제안한다. output matrix O와 아까 tiled softmax 계산을 위해 필요했던 m(x), l(x)를 이용해 recomputation하는 것이 가능하다!

위의 방법은 training backward propagation에서 memory ↔ computation cost를 trade-off하는 방법인데, trainig at scale에서 많이 사용되는 방법인 activation checkpointing과 같은 철학을 공유하는 것이다. 연산량(FLOPs)는 늘어나지만, memory usage와 access횟수를 줄이게 됨으로써 wall-clock time을 줄이게 된다.

참고) activation checkpointing

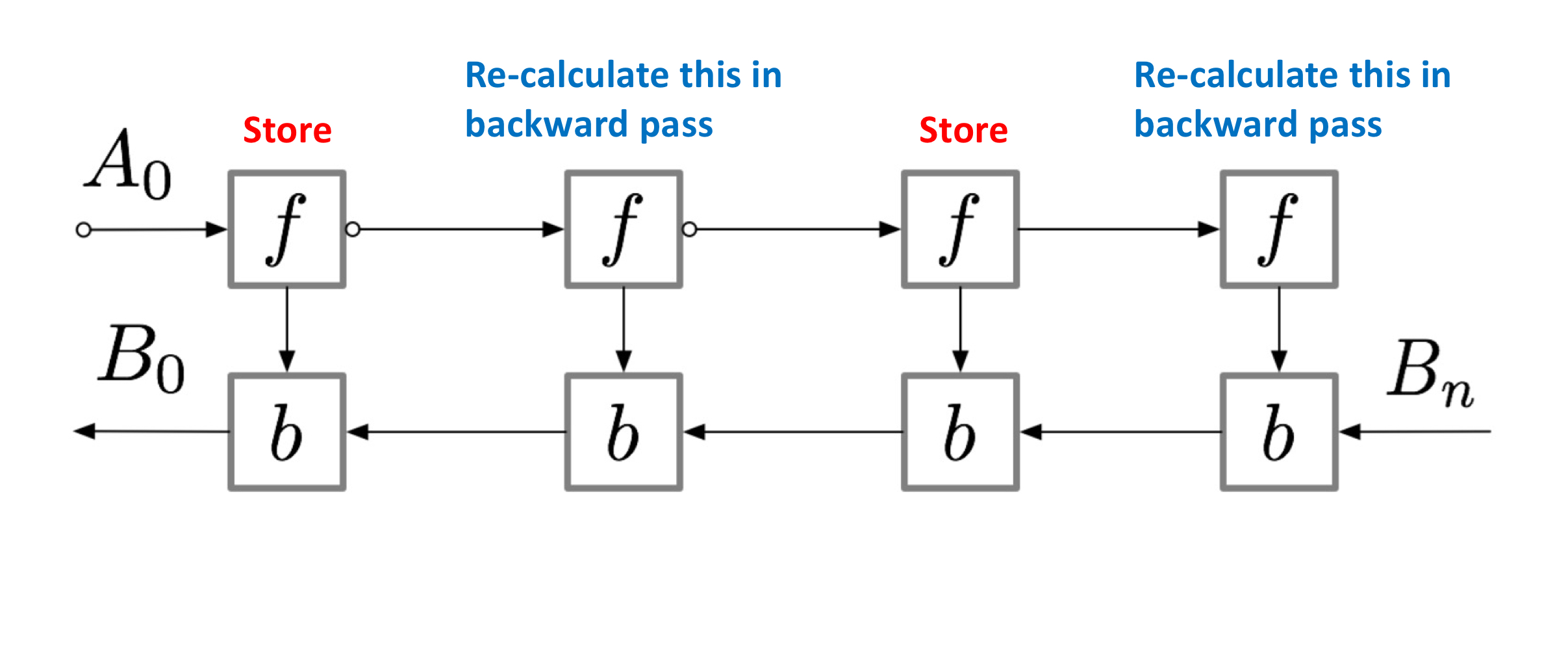
Implementation details: Kernel fusion

위 알고리즘은, exact self-attention output $O=softmax(QK^T)V$ 를 계산하기 위해 $O(N^2d)$ 만큼의 FLOPs와 $O(N)$ 의 additional memory를 요구한다.

Analysis: IO complexity of FlashAttention

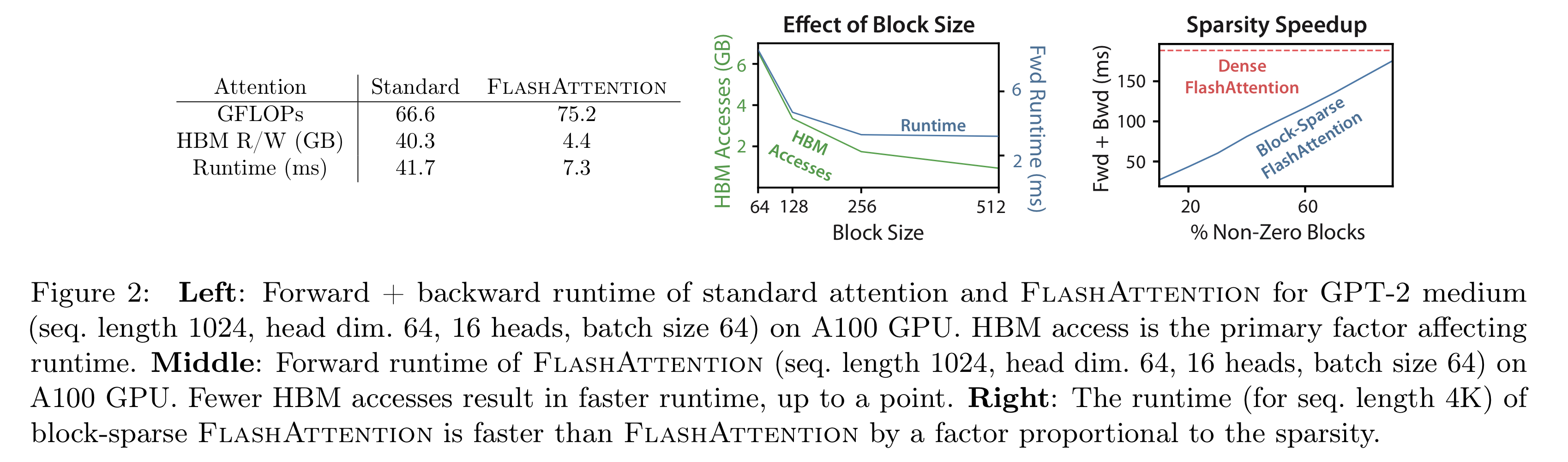
standard attention과 flashattention을 비교하자면, sequence length N, head dim d, SRAM size M에 대해 Standard attention은 $\Theta(Nd +N^2)$ 의 HBM access를, FlashAttention은 $\Theta(N^2d^2M^{-1})$ 의 HBM access를 요구한다. 보통의 경우인 $d=(64-128), M\approx 100KB$ 를 생각하면, standard에 비해 HBM access를 많은 양 줄였다고 말할 수 있다.

Experiments

논문 참조 고고

Limitations and Future Directions

Compiling to CUDA

IO-Aware implementation을 위해서 새로운 CUDA kernel을 짜는 것이 요구된다. Pytorch보다 더욱 low-level programming이 필요함.. 또한 그 구현이 다양한 GPU Architecture(Compute capability)에 따라 portability issues가 발생할 수 있다…

IO-Aware Deep Learning

우리의 work이 IO-awareness 자체에 대한 영감을 주면 좋겠다. transformer에서 attention모듈은 매우매우매우 memory intensive한 일인데 딱히 이를 지원하는 것이 없다는 게 문제.

Multi-GPU IO-Aware Methods

본 논문의 algorithm은 single GPU에서의 optimal이다. 최근 training at scale에선 다양한 Parallelism(MP, DP, PP)를 exploit 하는것이 중요한데, 이는 further work…로 남겨둔다.

본 논문을 정리하는 이 시점에 이미 FlashAttention-2가 공개되었는데, 어떻게 limitation을 해결했는지 다음 포스팅에서 알아보도록 하자. 그리고 Appendix도 정리해 올리면 좋겠다.(할 수 있을까?)

Sonny020402

Hi!

이전 포스트

Swin Transformer: hierarchical Vision Transformer using Shifted Windows

2개의 댓글

happy

2023년 7월 21일

글 잘 읽었습니다. Transformer의 model size와 memory complexity에 대한 설명이 흥미로웠습니다. 특히, FLASHAttention을 통해 GPU HBM의 read/write transaction을 줄이는 접근법이 인상적이었습니다. 또한, 논문의 limitation과 future direction에 대한 설명도 흥미롭게 읽었습니다. 블로그에 올려주신 이 글을 통해 많이 배우게 되었습니다. 감사합니다.

1개의 답글