In this post, I will organize the contents of chapter 3. In the chapter 3, there are some operations.
- Addition
- Subtraction
- Multiplication
- Division
- Floatin-point representation and operation
Addition
If we want to add some binary number to other binary number, we can just add. However, there are some points that we must be careful.
Positive number + Positive number
Negative number + Negative number
In that cases, it might occur Overflow. It means that the result of this expression is out of range. In first case, it should be a positive number, but if the overflow is occurred, then result is negative number. On the other hands, in the second cases, if the result is positive number, then there is a overflow.
Subtraction
Subtraction can be expressed by using add and 2's complement. If we want to evaluate 7-6, then we just express 6 by using 2's complement, and we add two integers. By doing that we can get result.
However, if we do subtraction, there is a posibility of overflow.
Positive integer - Positive integer
-> not overflow
Negative integer - Negative integer
-> not overflow
Subtracting + from -
-> If the result's sign is 0, then it is overflow
Subtracting - from +
-> If the result's sign is 1, then it is overflow
Multiplication
There are three types of multiplication, but type 1 and type 2 are just sample for explain type 3. Therefore I will explain only type 3.
This is a type 3 multiplcation curcit. In this unit, multiplier is in the product(64-bits). By using it, we can save the space of CPU.
The logic of Multiplcation is simple. There are 32 bits of multiplier and 32 bits of 0s. If the multiplier's last value is 1, then we just add multiplicand to 32bits of 0s. Otherwise, we don't add it. Next, we have to shift bits to right.
There is a case that 32-bits of product's hi points add with multiplicand, it can be carry out. In this case, after shifting bits, we have to add 1 in first bit.
We should repeat it 32 times.
Division
Division is more difficult rather than Multiplication.
We have to use Hi and Lo register in Division.
- Hi Register : stores Remainder
- Lo Register : stores Quotient
The flow of division can be divided several steps.
- Shift left
- Subtract
- If the result is negative, then put 0 in the last of them. If the result is positive, then put 1 in the last of them.
- If the result is negative, then we have to restore them, but the result is positive, then we don't.
If we repeat 32 times, there is a result.
Floating point number
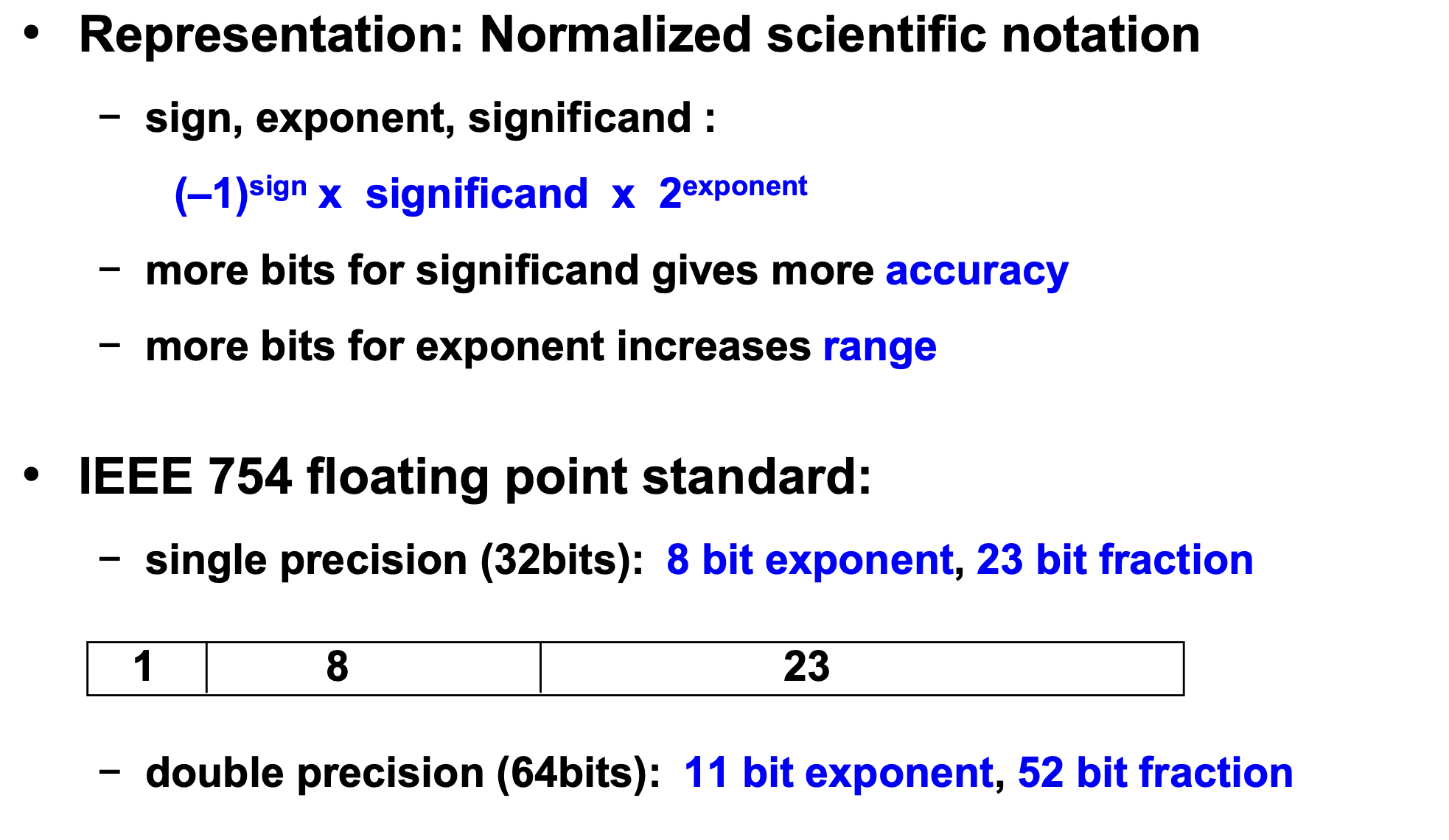
IEEE 754 is a rule to express floating point number. Ther e are 3 section, sign, significand, and exponent.
In the computer architecture, there are 8 bits to express exponent. So, we can use 0-256 numbers. To express negative integer, IEEE 754 use bias of 127.
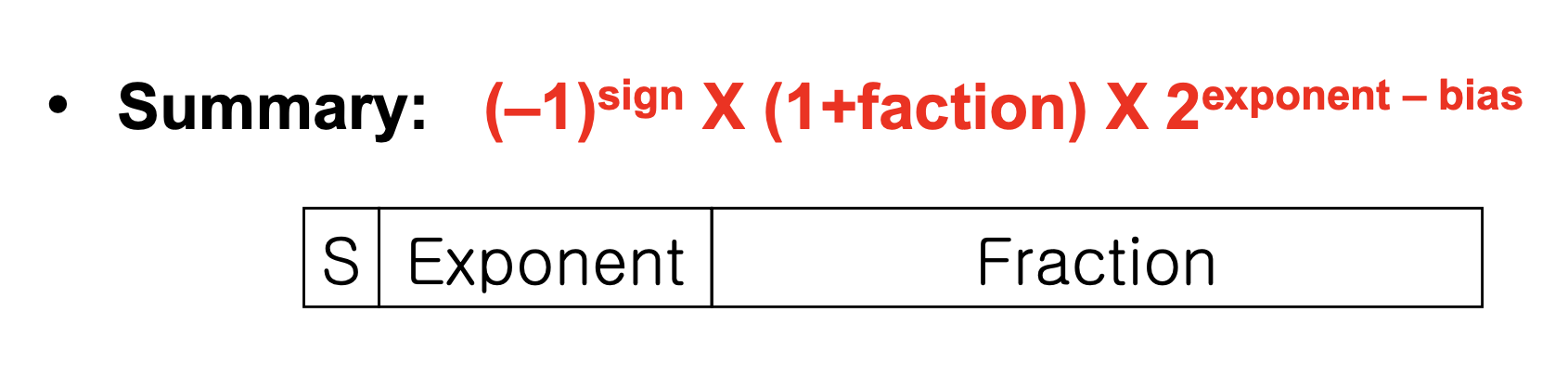
IEEE assumes that there must be 1 in front of fraction section. So, it just skipped to use 1.
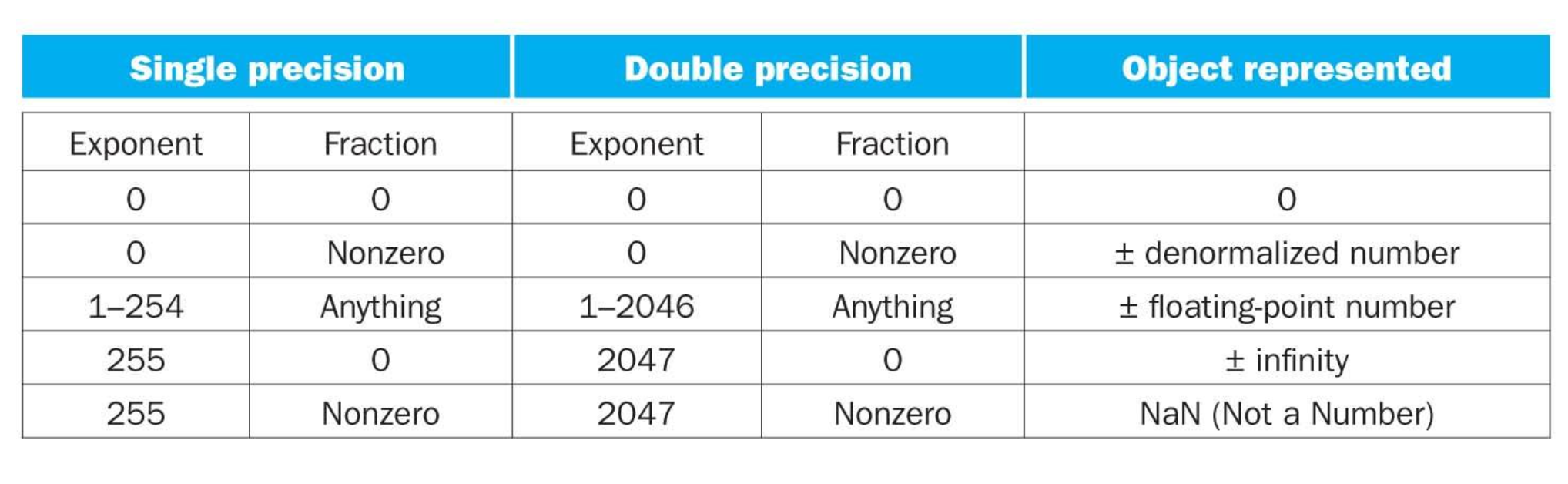
This is the range of the IEEE. All of the elements are 0, it is express 0. If Exponent is 255, and fraction is 0, then it represented infinity.
If the Exponent's value is 255 and fraction is Nonzero, then it is represented NAN.
In addition, there is a concept of underflow.
The minimum value of Exponent is approx 2^-23. So, we can represent at most 2^-23. If there is more small integer, we can't express it by using IEEE 754.
