오늘의 목표
- 개인의 가설검정에 필요한 컬럼과 초기 군집 갯수를 넣어 클러스터링 진행 후 성능 보기
- 실루엣 계수, WCSS, scatterplot
- 엘보우 방법, 실루엣 분석으로 최적의 군집 갯수 찾기
- 1번에서 했던 기본 모델과 최적의 클러스터 모델에 대해서 성능 비교
- 실루엣 계수, WCSS, scatterplot
- 마지막으로 더 좋았던 모델에 대해 군집 특징 생각하기.
사실 내가 전처리 했던 것들을 발표에서 사용할 수 있게 다듬는 작업을 하다보니까 머신러닝 단계에 들어갈 시간이 없었다. 따라서 오늘은 내가 한 작업이 아닌 팀원분들의 모델링 결과를 공유해보려고 한다.
모델링 및 성능 측정 가이드
모델링은 못했지만, 팀원분들께서 어떤 방향성으로 진행하면 좋을지에 대한 가이드를 전에 했던 머신러닝 과제를 참고하여 제작해서 공유드렸다. 가이드는 다음과 같다:
- 개인의 가설검정에 필요한 컬럼과 초기 군집 갯수를 넣어 클러스터링 진행 후 성능 보기
- 실루엣 계수, WCSS, scatterplot
- 엘보우 방법, 실루엣 분석으로 최적의 군집 갯수 찾기
- 1번에서 했던 기본 모델과 최적의 클러스터 모델에 대해서 성능 비교
- 실루엣 계수, WCSS, scatterplot
- 마지막으로 더 좋았던 모델에 대해 군집 특징 생각하기.
- k-means 사용 예시
from sklearn.cluster import KMeans # 클러스터의 개수가 2개일 때 model_kmeans1 = KMeans(n_clusters=2, init='k-means++', max_iter=300, random_state=42) model_kmeans1.fit(iris_df) # 클러스터 예측 결과1 (레이블) 추출 cluster1 = model_kmeans1.labels_ iris_df['cluster1'] = cluster1 iris_df.head(5) - 시각화(위에서 만든 두 군집화 모델 비교)
plt.figure(figsize=(12, 6)) plt.subplot(1, 2, 1) sns.scatterplot(data=iris_df, x='sepal length (cm)', y='sepal width (cm)', hue='cluster1') plt.title('Cluster (2)') plt.subplot(1, 2, 2) sns.scatterplot(data=iris_df, x='sepal length (cm)', y='sepal width (cm)', hue='cluster2', palette='viridis') plt.title('Cluster (3)') plt.show - 최적의 클러스터 개수 찾기(엘보우, 실루엣)
-
elbow method: K-means 알고리즘을 실행할 때, 클러스터 개수(K)를 점차 증가시키면서 클러스터링을 수행하고, 이에 따른 SSE(Sum of Squared Errors) 값을 계산하여 그래프로 나타내어 최적의 K값을 선택하는 방법. -
silhouette analysis: 데이터 포인트가 속한 클러스터의 일관성을 측정하여 최적의 K값을 찾는 방법. 각 데이터 포인트의 실루엣 계수를 계산하여, 전체 데이터 포인트의 평균 실루엣 계수를 구한다. 실루엣 계수는 클러스터의 일관성을 나타내며, 값이 높을수록 클러스터링 결과가 좋다는 것을 의미.elbow method:
# 엘보우 방법을 사용하여 최적의 K값 탐색 def elbow(X): sse = [] for k in range(1, 11): kmeans = KMeans(n_clusters=k, init='k-means++', max_iter=300, random_state=42) kmeans.fit(X) sse.append(kmeans.inertia_) return sse sse = elbow(iris_df) # SSE 그래프 그리기 plt.plot(range(1, 11), sse, marker='o') plt.xlabel('Number of clusters') plt.ylabel('SSE') plt.show()silhouette analysis:
from sklearn.metrics import silhouette_score # 실루엣 분석을 사용하여 최적의 K값 탐색 silhouette_scores = [] for k in range(2, 11): kmeans = KMeans(n_clusters=k, init='k-means++', max_iter=300, random_state=42) kmeans.fit(iris_df) score = silhouette_score(iris_df, kmeans.labels_) silhouette_scores.append(score) # 실루엣 분석 그래프 그리기 plt.plot(range(2, 11), silhouette_scores, marker='o')
-
- 클러스터링의 성능 측정(실루엣 계수, WCSS)
실루엣 계수 (Silhouette Coefficient)-
클러스터가 얼마나 잘 분리되었는지를 평가하는 지표
-
값은 -1에서 1 사이이며, 1에 가까울수록 각 클러스터가 잘 분리된 것을 의미
# 군집 2개일 때 # 여러분의 초기 클러스터 모델을 cluster1에 넣으시면 됩니다. silhouette_1 = silhouette_score(iris_df, cluster1) print(f'클러스터 개수 2개일 때: Silhouette Score = {silhouette_1:.4f}')# 군집 3개일 때 silhouette_2 = silhouette_score(iris_df, cluster2) print(f'클러스터 개수 3개일 때: Silhouette Score = {silhouette_2:.4f}')평균 군집 내 SSE (Within-cluster Sum of Squares, WCSS)각 클러스터 내 데이터 포인트가 해당 클러스터의 중심에서 얼마나 떨어져 있는지를 측정
이 값이 작을수록 같은 클러스터 내의 데이터 포인트들이 중심에 가깝게 모여 있음을 의미
# 군집 2개일 때 wcss_1 = model_kmeans1.inertia_ print(f'클러스터 개수 2개일 때: WCSS = {wcss_1:.4f}')# 군집 3개일 때 wcss_2 = model_kmeans2.inertia_ print(f'클러스터 개수 3개일 때: WCSS = {wcss_2:.4f}')
-
모델링 결과
가설 설정
고객의 재구매 횟수가 높을수록 매출에 긍정적인 영향을 미칠 것이다
kmeans 사용 이유
- 다양한 항목들이 들어가기 때문에 해당 항목들의 거리를 보고 군집을 진행하는 것이 더 의미있다고 생각함
클러스터링에 사용할 컬럼
merged_df['repeat_order'] = merged_df.groupby('customer_id')['order_id'].transform('nunique')
merged_df['total_price'] = merged_df.groupby('customer_id')['price'].transform('sum')
merged_df['avg_price'] = merged_df.groupby('customer_id')['price'].transform('mean')
merged_df['total_payment_value'] = merged_df.groupby('customer_id')['payment_value'].transform('sum')
merged_df['avg_payment_value'] = merged_df.groupby('customer_id')['payment_value'].transform('mean')
merged_df['delivery_time'] = merged_df['order_delivered_timestamp'] - merged_df['order_purchase_timestamp']
merged_df['delivery_estimated_time'] = merged_df['order_estimated_delivery_date'] - merged_df['order_purchase_timestamp']
merged_df['delivery_gab'] = merged_df['delivery_estimated_time'] - merged_df['delivery_time']컬럼별 상관관계 파악
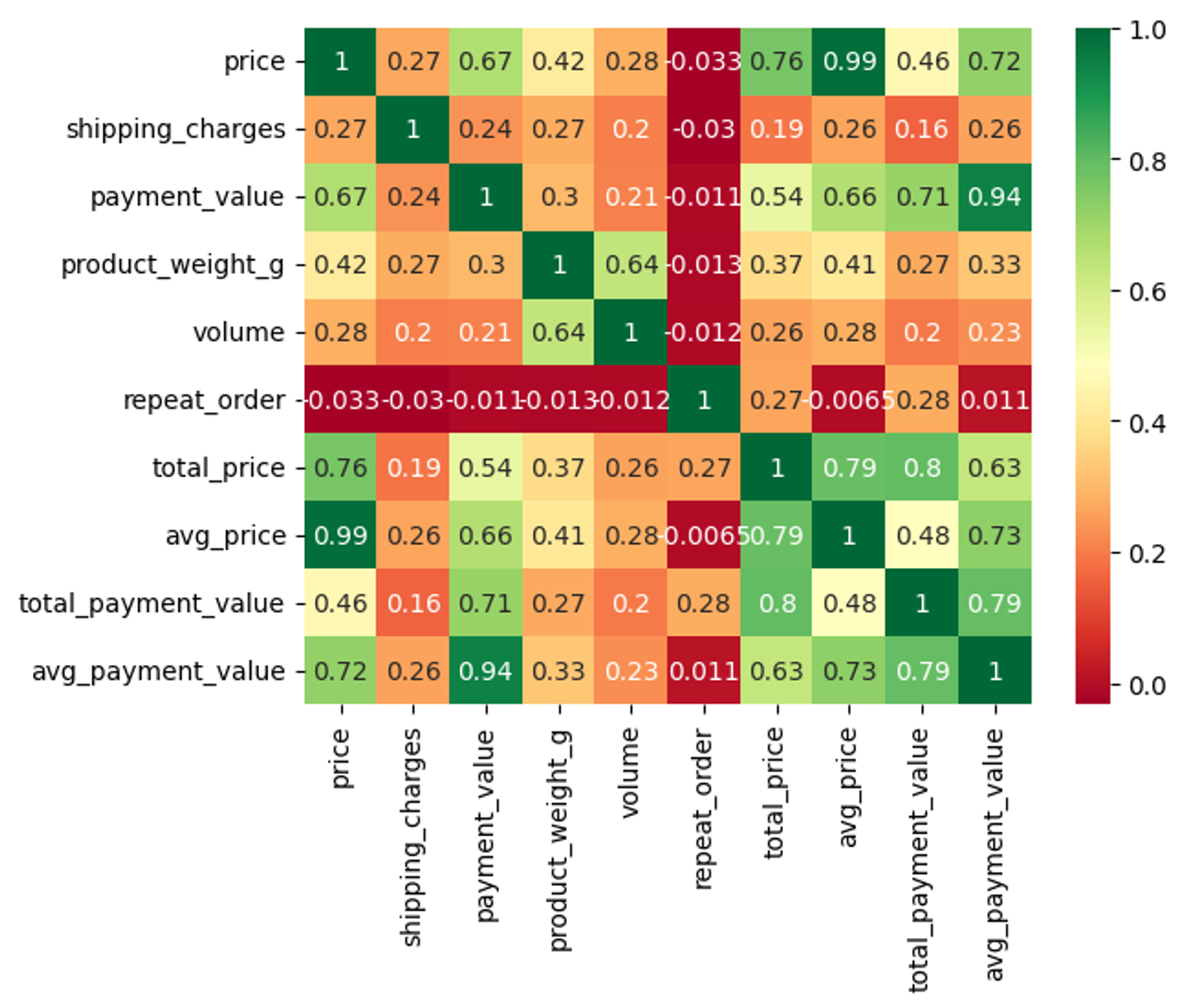
클러스터 최종 항목 설정
repeat_order,total_price,total_payment_value,avg_price,avg_payment_value- 선정 이유:
- 고객 특성에 관련된 항목을 방문 횟수, 총구매액, 평균 금액으로 선정하였음
- 컬럼과 상관관계가 0.5 이상인 경우 삭제함
price와total price도 상관관계가 높았는데 초기 목표에는 총 금액 고객별 구매액이 군집에 유의미하기에 채택함
→payment value도 동일함total과avg의 상관관계가 특히 높았는데 이런 경우 합산을 쓰는 것이 맞다고 생각하여total을 채택함.
클러스터 결과
# 클러스터에 넣을 항목 설정
cluster_1 = merged_df[['repeat_order','total_price', 'avg_price', 'total_payment_value', 'avg_payment_value']]
# 학습할 데이터와 시각화 데이터를 따로 나누기
cluster_1_clu = cluster_1.copy()
from sklearn.cluster import KMeans
# 군집 2개로 나누기
custoemr_kmeans2 = KMeans(n_clusters=2, init='k-means++', max_iter=300, random_state=42)
custoemr_kmeans2.fit(cluster_1)
cluster_1_clu['cluster2'] = custoemr_kmeans2.labels_
# 군집 3개로 나누기
custoemr_kmeans3 = KMeans(n_clusters=3, init='k-means++', max_iter=300, random_state=42)
custoemr_kmeans3.fit(cluster_1)
cluster_1_clu['cluster3'] = custoemr_kmeans3.labels_
# 군집 4개로 나누기
custoemr_kmeans4 = KMeans(n_clusters=4, init='k-means++', max_iter=300, random_state=42)
custoemr_kmeans4.fit(cluster_1)
cluster_1_clu['cluster4'] = custoemr_kmeans4.labels_
# 실루엣 계수
from sklearn.metrics import silhouette_score
labels = custoemr_kmeans2.fit_predict(cluster_1)
silhouette_1 = silhouette_score(cluster_1, custoemr_kmeans2.labels_)
print(f'클러스터 개수 2개일 때: Silhouette Score = {silhouette_1:.6f}')
from sklearn.metrics import silhouette_score
labels = custoemr_kmeans3.fit_predict(cluster_1)
silhouette_2 = silhouette_score(cluster_1, custoemr_kmeans3.labels_)
print(f'클러스터 개수 3개일 때: Silhouette Score = {silhouette_2:.6f}')
from sklearn.metrics import silhouette_score
labels = custoemr_kmeans4.fit_predict(cluster_1)
silhouette_3 = silhouette_score(cluster_1, custoemr_kmeans4.labels_)
print(f'클러스터 개수 4개일 때: Silhouette Score = {silhouette_3:.6f}')
# 시각화
plt.figure(figsize=(30,10))
plt.subplot(1,3,1)
sns.scatterplot(data=cluster_1, x='total_price', y='total_payment_value', hue='cluster2')
plt.subplot(1,3,2)
sns.scatterplot(data=cluster_1, x='total_price', y='total_payment_value', hue='cluster3')
plt.subplot(1,3,3)
sns.scatterplot(data=cluster_1, x='total_price', y='total_payment_value', hue='cluster4')- kmeans 결과:
군집 개수 실루엣 계수 WCSS N = 2 0.4541 2969.7368 N = 3 0.3721 2244.7876 N = 4 0.3897 1804.0762 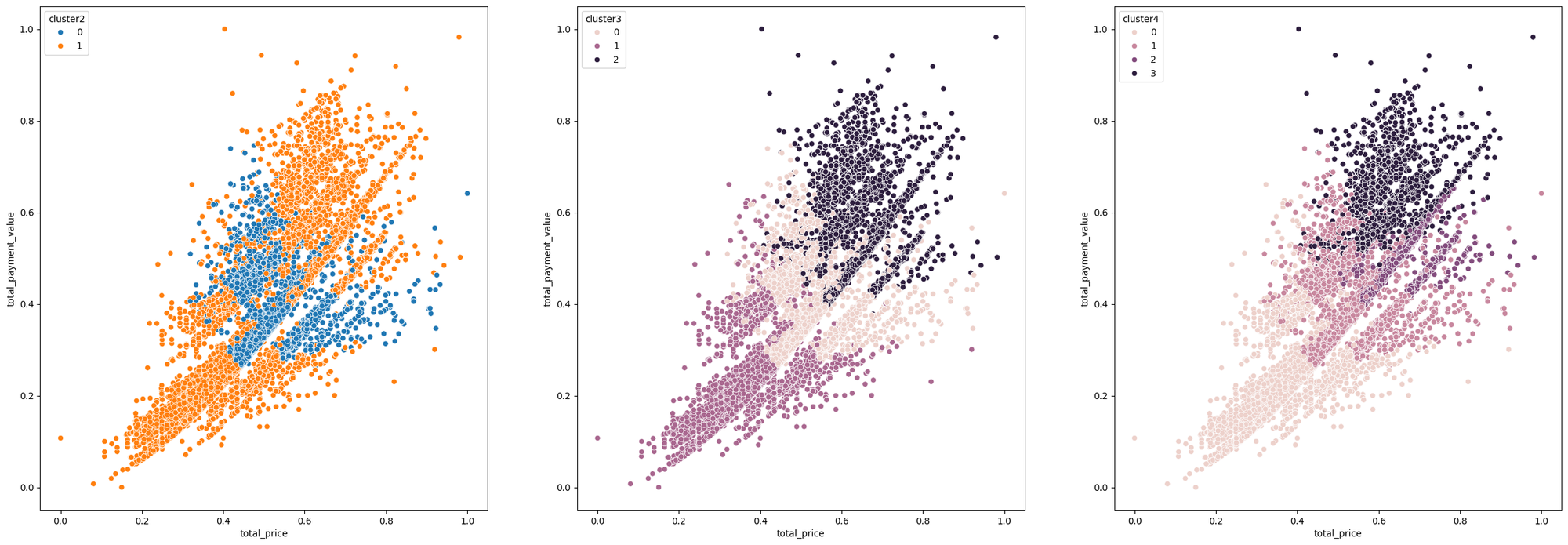
최적의 군집 개수 찾기
엘보우 방법을 통한 최적의 클러스터 개수 탐색
def elbow(df):
sse = []
for i in range(1,15):
km = KMeans(n_clusters= i, init='k-means++', random_state=42)
km.fit(df)
sse.append(km.inertia_)
plt.plot(range(1,15), sse, marker = 'o')
plt.xlabel('cluster count')
plt.ylabel('SSE')
plt.show()
elbow(cluster_1)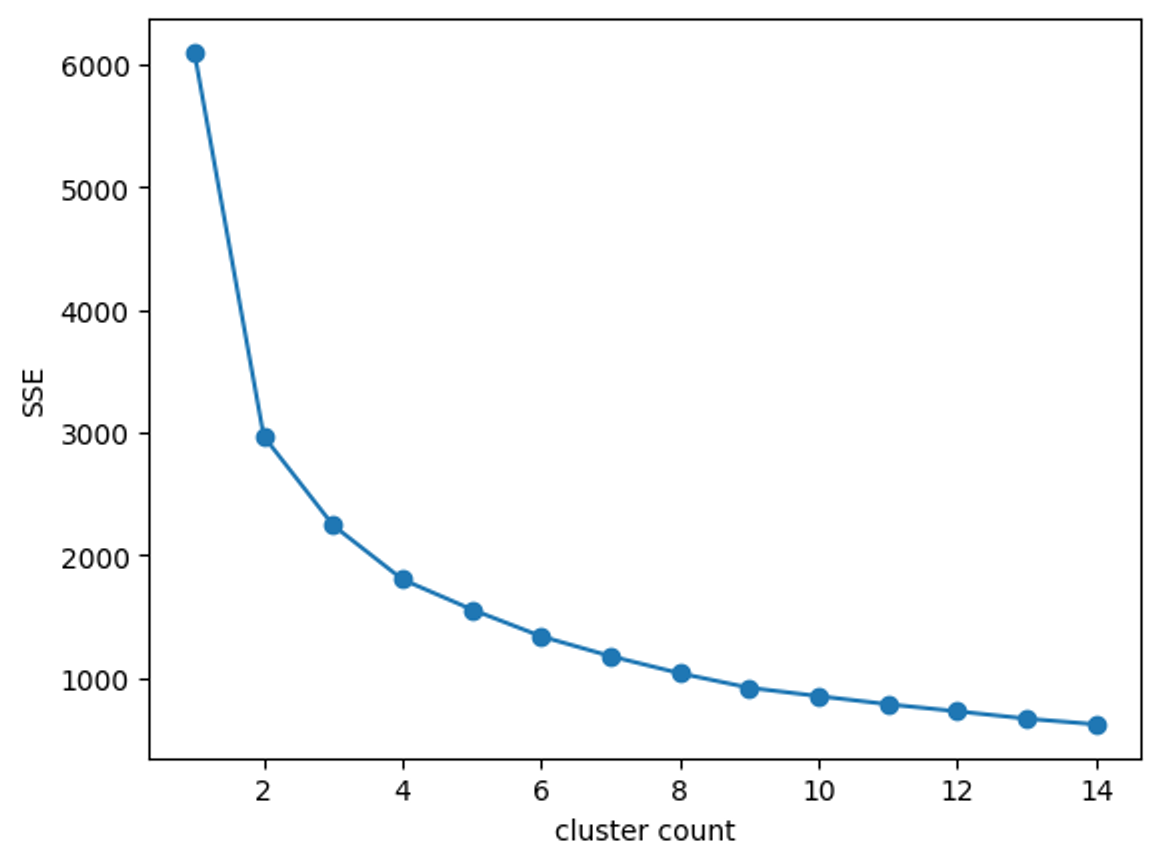
최종 모델링 결과
kmeans사용 이유 : 클러스트의 항목을 넣었을 때 가장 실루엣 계수가 좋았으며, WCSS 계수가 잘 나온 편이라서n_clusters = 3을 사용 이유 : 실루엣 계수에서는 확실히 2가 더 잘 나오긴 했지만, 엘보우 포인트나 WCSS 계수를 보고 3개의 군집으로 나눈 것이 군집간 특성을 파악하는데 더 유의미하다고 생각함
# 클러스터에 넣을 항목 설정
cluster_1 = merged_df[['repeat_order','total_price', 'avg_price', 'total_payment_value', 'avg_payment_value']]
# 학습할 데이터와 시각화 데이터를 따로 나누기
cluster_1_clu = cluster_1.copy()
from sklearn.cluster import KMeans
# 군집 3개로 나누기
custoemr_kmeans3 = KMeans(n_clusters=3, init='k-means++', max_iter=300, random_state=42)
custoemr_kmeans3.fit(cluster_1)
cluster_1_clu['cluster3'] = custoemr_kmeans3.labels_
# 실루엣 계수
from sklearn.metrics import silhouette_score
labels = custoemr_kmeans3.fit_predict(cluster_1)
silhouette_2 = silhouette_score(cluster_1, custoemr_kmeans3.labels_)
print(f'클러스터 개수 3개일 때: Silhouette Score = {silhouette_2:.6f}')
# 시각화
plt.figure(figsize=(30,10))
plt.subplot(1,3,1)
sns.scatterplot(data=cluster_1, x='total_price', y='total_payment_value', hue='cluster2')
plt.subplot(1,3,2)
sns.scatterplot(data=cluster_1, x='total_price', y='total_payment_value', hue='cluster3')
plt.subplot(1,3,3)
sns.scatterplot(data=cluster_1, x='total_price', y='total_payment_value', hue='cluster4')- 결과:
군집 개수 실루엣 계수 WCSS N = 2 0.4541 2969.7368 N = 3 0.3721 2244.7876 N = 4 0.3897 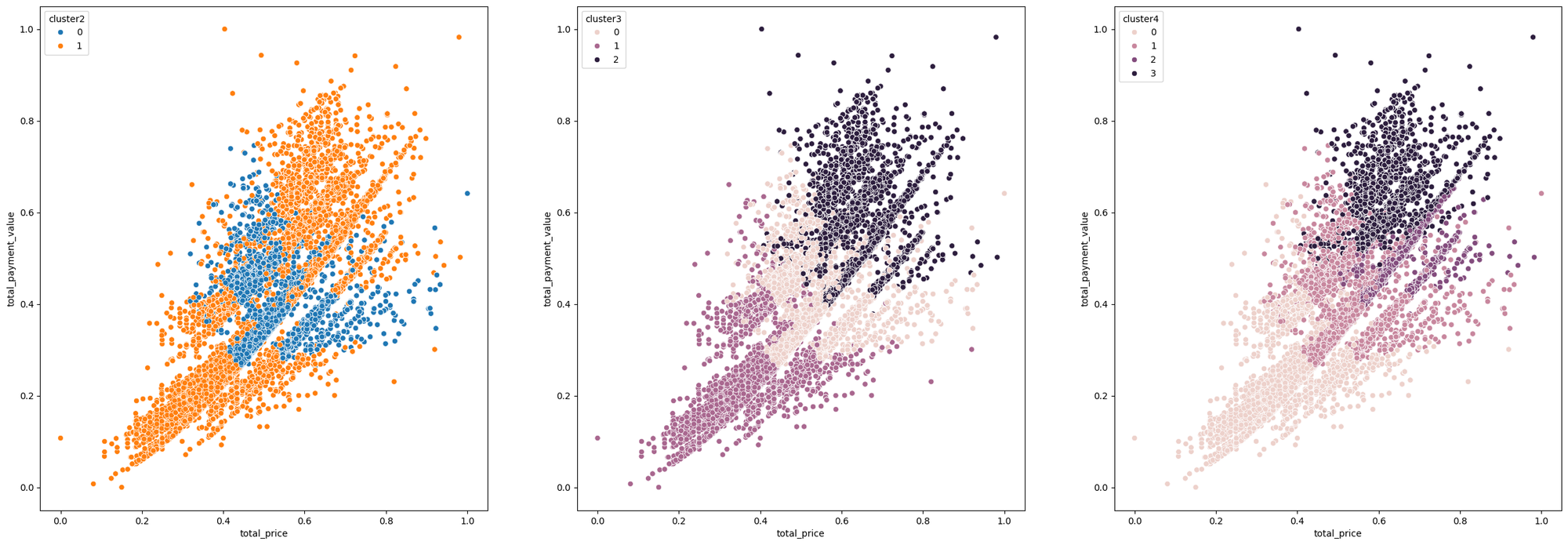
내일 할 일
- 군집 결과 해석
- 군집별 페르소나 만들기
- 최종 발표 자료 정리
