[Data] 데이터 분석 및 시각화02

review

수치형 변수는 크기를 비교할 수 있는 연속적인 숫자를 갖는 변수이다.

1. x만 사용하는경우는 y는 자동으로 수치형 변수를 선택하도록 두는 경우입니다. 이때 x는 각범주를 나타내고 범주에 대해 수치형 데이터의 분포를 보여줍니다.

2. x와 y 매개변수 둘다 사용하는경우는 범주형 변수와 수치형 변수 간의 관계를 시각화합니다. 일반적으로 x는 범주형 변수를 나타내고 y는 수치형 변수를 나타내게 됩니다.

3. hue매개변수와 survivied 컬럼을 두는 경우 의미의 차이는?
   hue 매개변수는 범주형 변수로 각 그룹을 색상으로 구분하고 특정 범주에 대해 비교를 더 명확히 할 수 있도록 도와줍니다. suervived에 따라 색상을 다르게 표기함으로써 각 클래스 내에서 분포차이를 비교 할 수 있습니다.

05 단별량 분석

05.1. 단변량 분석 ① - 수치형

1. 환경준비

2. 수치화

• round() : 몇번째자리에서 반올림한다.
• mean() : 평균을 구한다.
• median() : 가장 가운데 위치한 중앙값
• mode() : 가장 빈번하게 나타나는 최빈값

titanic['Pclass'].mode()[0]
titanic['Pclass'].value_counts().idxmax()

최빈값의 인덱스를 가져온다. value_counts()로 범주형의 값을 읽어와 index가 max인 값을 가져온다.

• describe() : 4분위수와 함께 기술 통계를 보여준다.
  
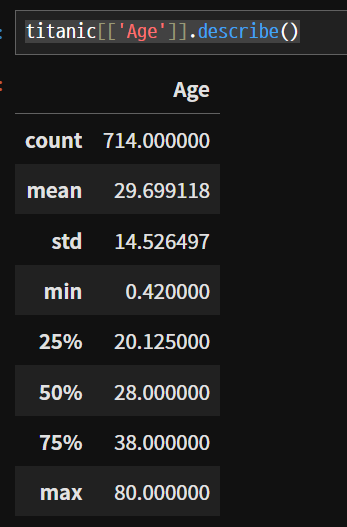
  시리즈를 [] 중괄호에 넣어주면 시리즈를 데이터프레임으로 만들어 줄 수 있다.
  
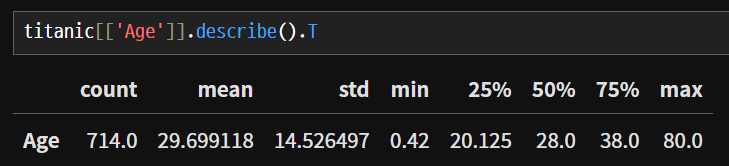
  시리즈는 .T 가 안되지만, 데이터프레임은 .T 를 사용하여 가로로 돌릴 수 있다.

3. 시각화

수치형 데이터는 분포와 흐름을 본다.

데이터의 분포는 히스토그램, density plot, box plot으로 확인한다.
histogram
히스토그램은 데이터의 분포를 확인하는 가장 기본적인 시각화 도구이다.

sns.histplot(x='Ozone', data=air)
plt.show()

sns.histplot(x=air['Temp'])
plt.show()

sns.histplot(air['Wind'])
plt.show()

다음은 모두 실행이 된다.

density plot
수치형의 데이터 분포, 밀도를 확인 한다.
Pandas로도 plot() 메소드에서 kind매개변수를 kde로 지정해서 그릴 수 있다.


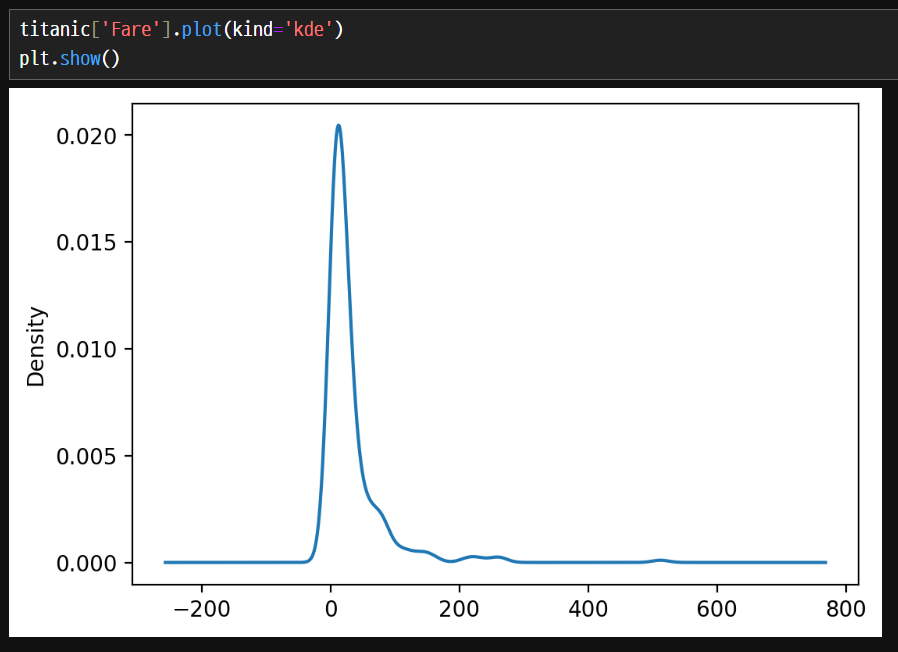
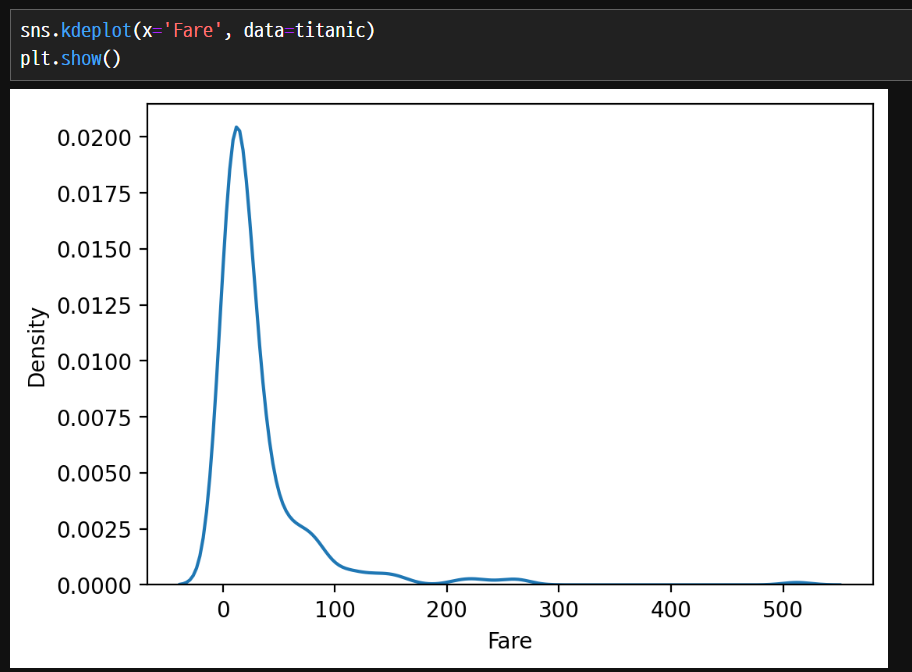
seaborn을 이용한 방법이 값이 길게 늘어지지 않고 깔끔하게 나온다.

확률밀도함수
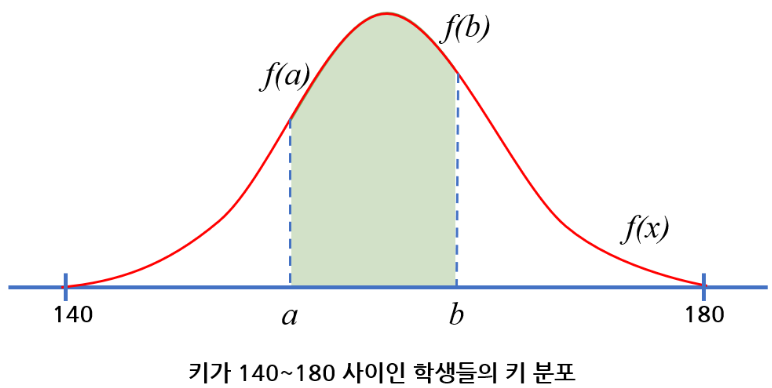
셀 수 있는 값의 분포(이산 확률 분포, 주사위)는 표로 표현할 수 있다.
셀 수 없는 값의 분포(연속 확률 분포, 학생들의 키)는 표로 표현할 수 없어 그래포로 표현한다.

a와 b사이의 확률을 구하고자 하면 그래프 아래의 색이 채워진 면적
정규분포의 확률
커널밀도함수는 실제 데이터에 대해서 그리기 때문에 정규분포와 다름

box plot
수치형의 데이터 분포를 확인 한다.
데이터의 결측치가 있으면 matplotlib은 그려지지 않는다. seaborn은 제외하고 그려준다.

plt.boxplot(x='Fare', data=titanic, vert=False)
plt.show()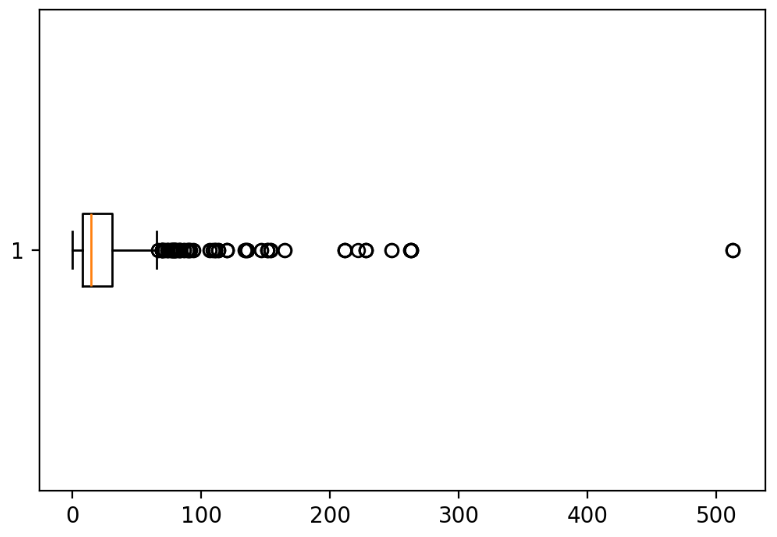

matplotlib으로 box plot를 그린다. 기본적으로 세로로 그래프가 그려지며 vert=False를 하면 가로로 그릴 수 있다. matplotlib은 y에 컬럼을 주면 오류가 발생한다.

sns.boxplot(x='Fare', data=titanic)
plt.show()

seaborn은 y에 컬럼을 주면 세로로 세울 수 있다.

sns.boxplot(x='Age', data=titanic,  width=0.2, color='w', medianprops={'color':'tab:orange'})
plt.axvline(titanic['Age'].mean(), color='r', linewidth=0.5, linestyle=':')
plt.show()

box plot에서는 평균이 표현되지 않는다. 평균은 따로 구해서 그려야 한다.

시계열 데이터 시각화
수치형의 데이터 분포를 확인 한다.
x축에 맞게 선 그래프로 표현한다.

• Matplotlib의 plot() 함수를 사용해 Line Plot을 그립니다.
• Seaborn의 lineplot() 함수를 사용해 Line Plot을 그립니다.

air['Date'] = pd.to_datetime(air['Date'])

plt.plot('Date', 'Ozone', data=air, label='Ozone')
plt.plot('Date', 'Temp', data=air, label='Temp')
plt.xlabel('Date')
plt.legend()
plt.show()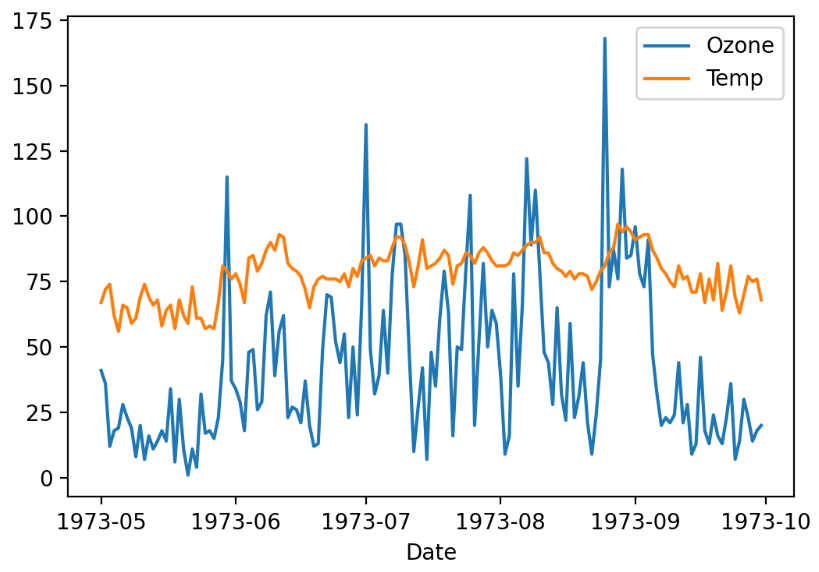

sns.lineplot(x='Date', y='Ozone', data=air, label='Ozone')
sns.lineplot(x='Date', y='Temp', data=air, label='Temp')
plt.legend()
plt.show()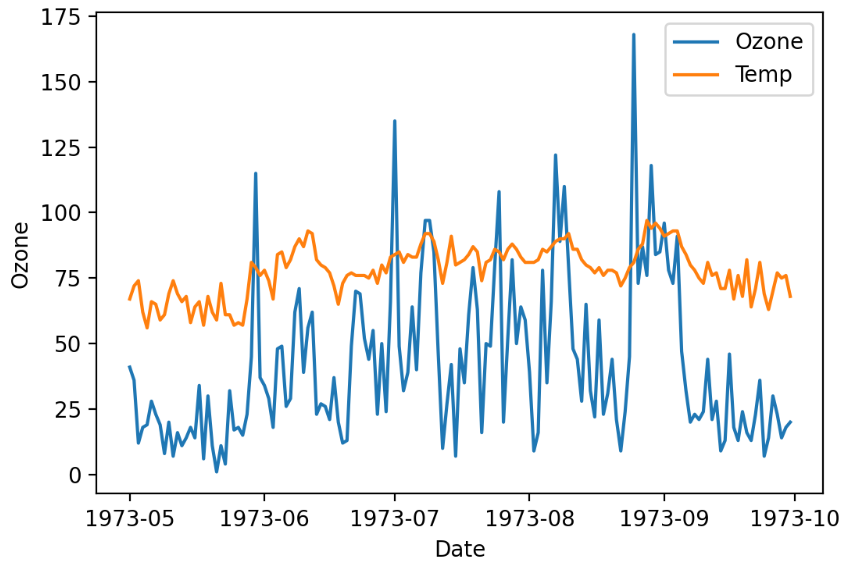

---

실습03

# 통게량
carseat[['Sales']].describe().T

변수들에 대해서 기초 통계량을 구한다.

# 시각화
plt.subplot(1,3,1)
sns.histplot(carseat['Sales'])

plt.subplot(1,3,2)
sns.kdeplot(carseat['Sales'])

plt.subplot(1,3,3)
sns.boxplot(carseat['Sales'])

plt.tight_layout()

변수들에 대해서 데이터를 시각화해서 나타낸다. 시각화는 sns.histplot(), sns.kdeplot(), sns.boxplot() 함수를 사용한다.

---

05.2. 단변량 분석 ② - 범주형

범주형 변수에는 정해진 몇 개의 값이 여럿 모여있는 변수이다.

• count로 볌주값이 몇개씩 있는지
• 전체에서 각각이 차지하는 비율은 어떤지

범주형 데이터로 살짝 변환하였음!

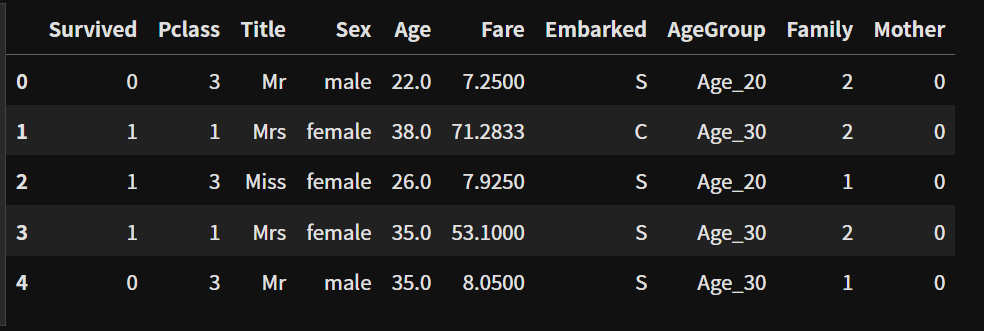
1. 수치화

value_counts()
value_counts() : 범주형 변수에 포함된 범주값 각각의 개수를 카운드

• normalize=True : 개수가 아닌 비율로 확인한다.

print(titanic['Pclass'].value_counts() / len(titanic))

normalize 매개변수를 사용하지 않고 len(데이터명)으로 데이터의 비율을 구할 수 있다.

• unique() : 범주값 자체를 확인한다.

titanic['Pclass'].unique()
# array([3, 1, 2], dtype=int64)

• sorted() : 정렬된 결과를 보여준다. 원본에 반영하지 않는다. (sort()는 정렬의 결과를 원본에 반환한다.)

sorted(titanic['Pclass'].unique())

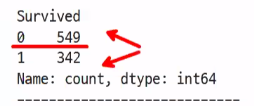
다음과 같을 때 머신러닝을 적용하면 1을 맞추는 확률부터 0을 맞추는 확률이 더 높다. 실제 데이터는 0이 대부분이고 1이 2% 밖에 되지 않는다. 실제 1은 기계고장 등에 대한 확률임으로 예측의 의미가 매우 크다.

col = 'AgeGroup'
print(titanic[col].value_counts())
print('-' * 20)
print(titanic[col].value_counts(normalize=True))

변수들의 빈도수와 비율을 구할 수 있다.

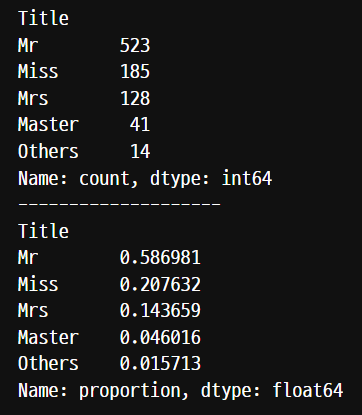
시리즈의 데이터 형태의 Name 값은 시리즈가 데이터프레임이 될 때 컬럼명이 된다.

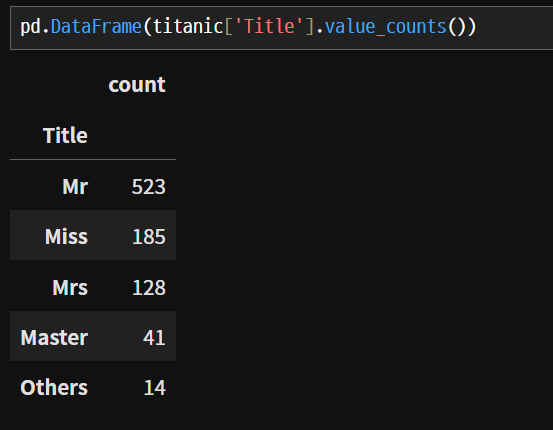
2. 시각화

범주형 데이터의 시각화는 count plot, bar plot, pie chart, heatmap를 통해 시각화한다.

bar plot
범주이름과 범주값이 필요하기 때문에 집계 작업(count)를 선행해야 한다.

• Pandas의 value_counts() 를 사용하여 집계합니다.
  • 집계 결과의 index: 범줏값 이름
  • 집계 결과의 values: 값

temp = titanic['Pclass'].value_counts()
temp
print(temp.index) # 범주값
print(temp.values) # 범주값 개수

데이터프레임에서 데이터명.index, 데이터명.values 로 범주값과 범주값 개수에 접근할 수 있다.

• bar() 함수로 시각화합니다.

temp = titanic['Pclass'].value_counts()

plt.bar(x=temp.index.astype(str), height=temp.values)
plt.show()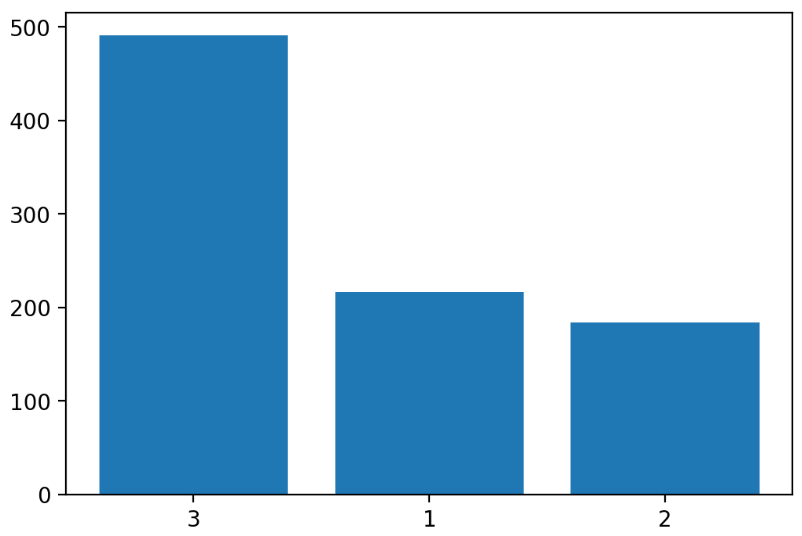

• 가로 그래프를 그릴 때는 barh()함수로 그려야 한다.

temp = titanic['Pclass'].value_counts()
plt.barh(y=temp.index.astype(str), width=temp.values)
plt.show()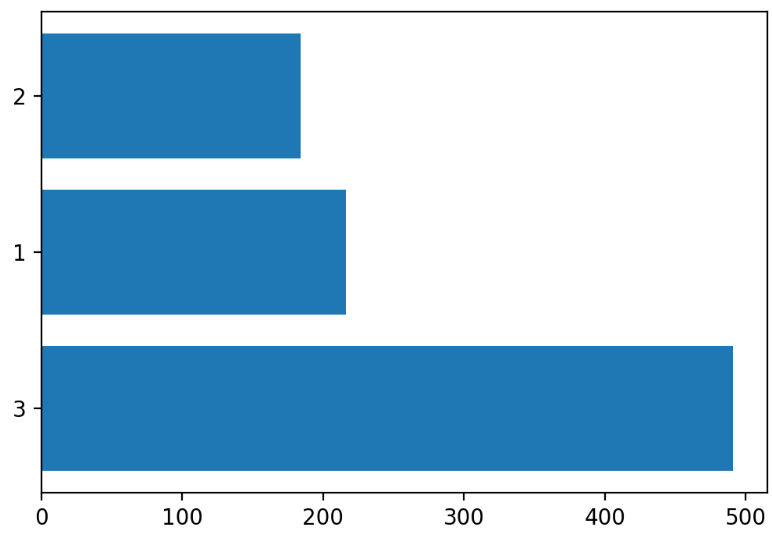

• seaborn에서는 count plot()으로 집계와 그래프를 함께 그려준다.

sns.countplot(x='Pclass', data=titanic)
plt.show()

matplolib으로 그린 barplot은 자동으로 count()가 큰값으로 정렬되고, seaborn은 값의 순서와 문자열의 경우 나타난 순서에 따라서 정렬된다.

pie chart

• 범주별 값의 빈도수가 아닌 비율을 비교할 때는 Pie Chart를 사용합니다.
  - x(값) : 범주값의 실제값이 비율로 내부에 작성된다.
  - labels : 외부에 작성되는 범주값이다.
  - autopct : 내부에 작성된는 값에 %를 달아준다.
• 파이의 각도와 방향을 조절할 수 있다.
  • startangle=90: 90도 부터 시작
  • counterclock=False: 시계 방향으로
• 파이 간격과 그림자를 조절할 수 있다.
  • explode=[0.05, 0.05, 0.05]: 중심으로 부터 1, 2, 3을 얼마만큼 띄울지
  • shadow=True: 그림자 추가

temp02 = titanic['Sex'].value_counts()
print(temp02.index)
print(temp02.values)

Pandas를 사용하여 pie chart를 그릴 때 value_counts로 먼저 집계를 하는 것이 필요하다. index와 values는 함수가 아니라 속성값으로 접근해야 하는 점을 주의한다.

plt.pie(x=temp02.values, labels=temp02.index, autopct='%1.f%%')
plt.show()

autopct를 설정해주지 않으면 내부에 적을 범주값의 실제값의 자료형을 지정해주지 않아서 작성되지 않는다. 주의하기!

---

실습

col = 'Urban'
temp=carseat[col].value_counts()
print(temp)
print('-'*20)
print(carseat[col].value_counts(normalize= True))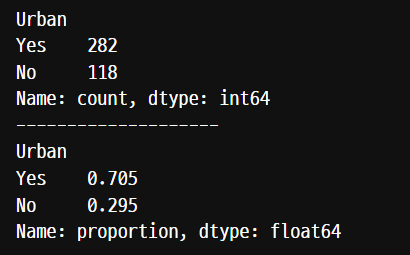

plt.subplot(1,2,1)
sns.countplot(x=carseat[col])

plt.subplot(1,2,2)
plt.pie(x=temp.values, labels=temp.index, autopct='%1.f%%')

plt.tight_layout()
plt.show()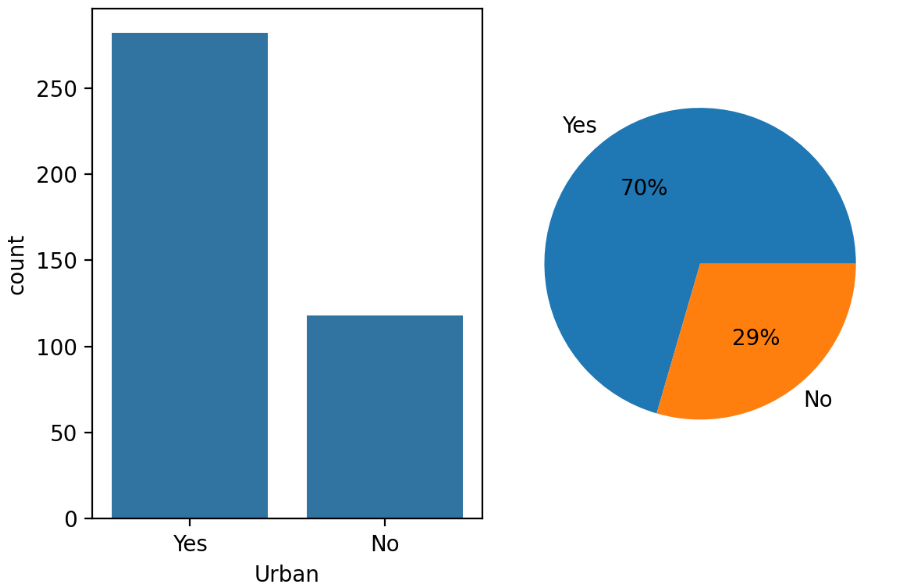

06. 이변량 분석

타이타닉 데이터에서 나이가 많을수록 요금이 많이 내는가?
두 변수 간의 관계를 살펴보기 위해 시각화와 수치화를 사용한다.

06.1. 이변량 분석 ① - 수치형 → 수치형

두 수치형 데이터 사이에서의 상관관계를 분석한다.

1. 시각화

두 수치형 변수의 관계를 시각화한다.

상관분석
상관분석은 수치형 변수x 에 대한 수치형 변수y 의 관계를 분석할 때 사용된다.

• 두 수치형 변수 관계는 산점도를 사용해 시각화한다.
• 두 수치형 변수의 관계를 비교할 때 직선(Linearity)를 중요하게 본다.

산점도
scatter plot(산점도)는 두 변수 간의 관계를 나타내는 그래프이다.

• 점들의 분포 형태를 통해서 두 변수 간의 상관관계를 파악한다.
• matplotlib의 scatter() 메서드를 통해서 산점도 그래프를 그릴 수 있다.
• 데이터의 폭이 얇을수록 강한 상관관계를 가진다.
• seaborn의 scatterplot() 메서드로 산점도 그래프를 그린다.

plt.scatter(x='Temp', y='Ozone', data=air, s=10, c='g')
plt.xlabel('Temp')
plt.ylabel('Ozone')
plt.show()

산점도의 marker와 color를 지정해 줄 수 있다.

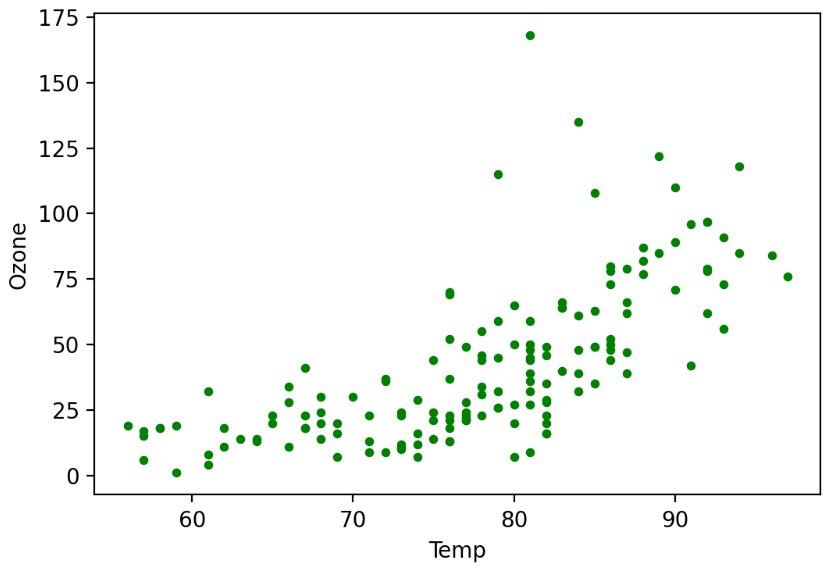
양의 상관관계를 가짐을 볼 수 있다.

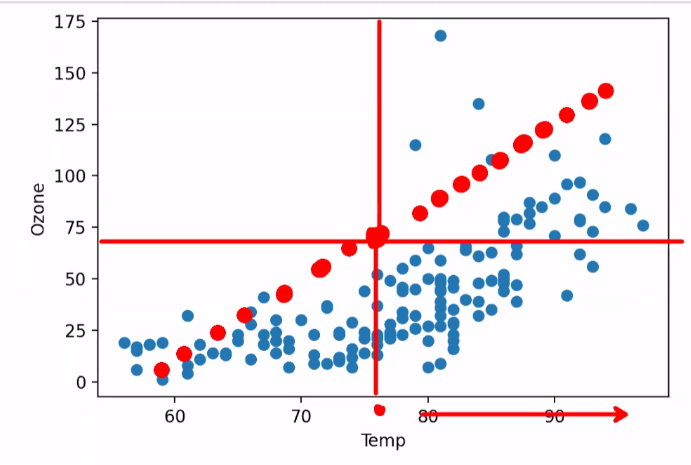
가운데 점에 대해서 오른쪽 아래의 위치한 데이터들은 강한 상관관계를 유지하지 않는다.

plt.scatter(x=air['Wind'], y=air['Ozone'])
plt.xlabel('Wind')
plt.ylabel('Ozone')
plt.show()

간략화하여 작성해 산점도 그래프를 그릴 수 있다. x값의 값이 유사한 컬럼들 사이에서는 2개의 그래프를 그릴 수 있다.

sns.scatterplot(x='Temp', y='Ozone', data=air)
plt.show()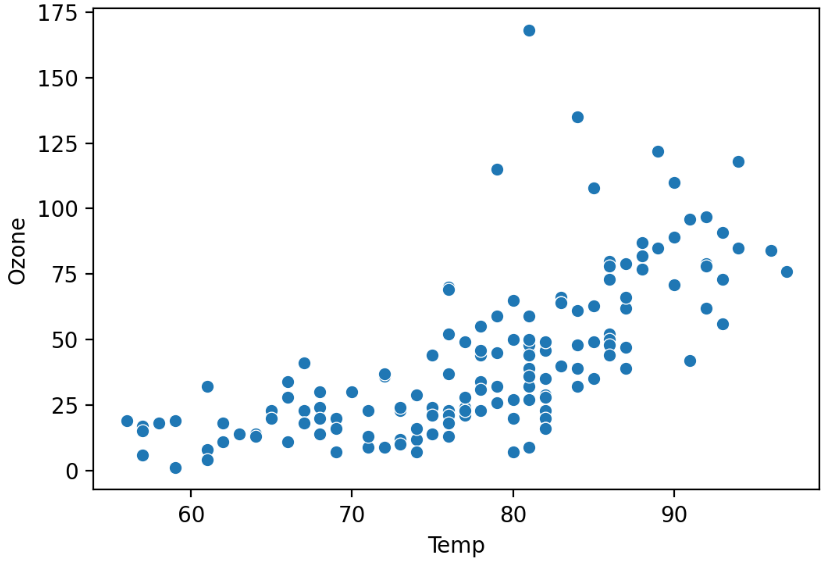

seaborn으로 그린 산점도에서는 겹치는 값이 edgecolor=white(기본값)으로 입체감있게 나타난다.

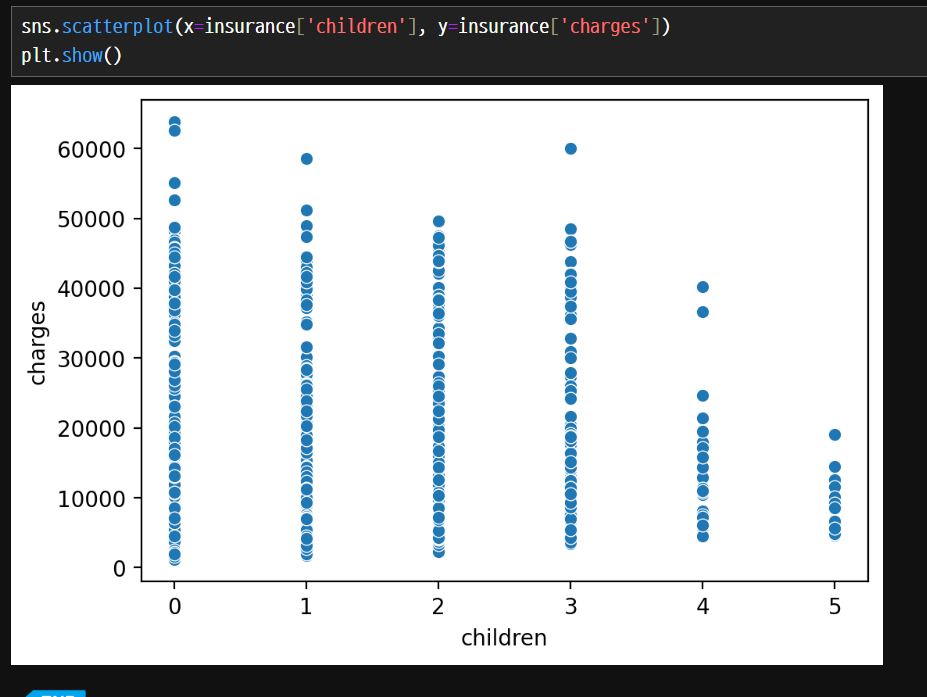
범주형 변수에 대해서 수치형 변수를 보았지만 의미적으로는 의미가 있다..

• 수치화만으로는 확인이 불가능할 수 있다.
• 시각화도 필요하다.

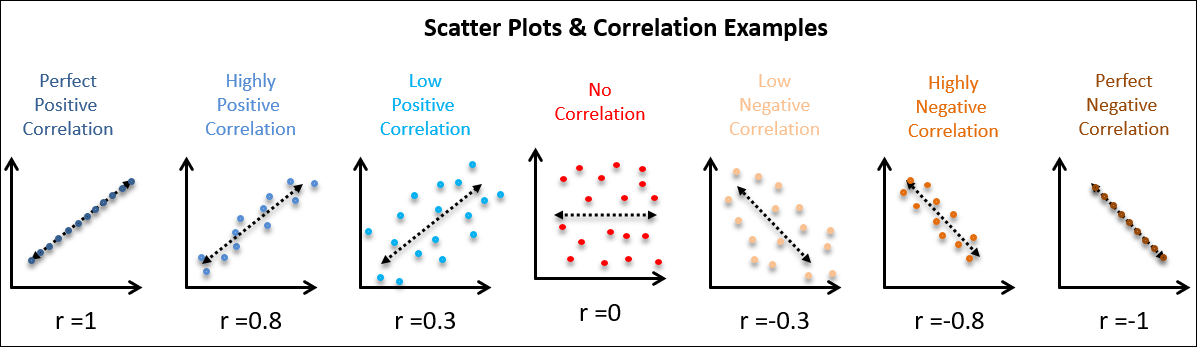
• 직선이고 오른쪽 위로 향할 때, 강한 양의 상관관계를 의미한다.
• 산점도의 폭에 따라서 강한지 약한지가 나타난다.
• 직선이고 왼쪽 아래를 향할 떄, 강한 음의 상관관계를 의미한다.

Pair plot

• Seaborn의 pairplot() 함수는 데이터프레임의 모든 숫자형 변수 쌍에 대한 산점도와 히스토그램을 같이 그려줍니다.
• pair plot은 수치형 변수에 대해서만 시각화한다.

sns.pairplot(air)
plt.show()

Joint plot

• Seaborn의 jointplot() 함수는 두 개의 변수 사이의 관계를 시각화하기 위한 유용한 도구입니다.
• 기본적으로 산점도를 그려주고, 히스토그램으로 각 변수의 분포를 보여줍니다.
• kind 매개변수를 사용하여 reg, hex, kde 등 다양한 형태의 그래프를 그릴 수 있습니다.

sns.jointplot(x='Solar.R', y='Ozone', data=air, kind='hex', marginal_kws=dict(bins=20))
plt.show()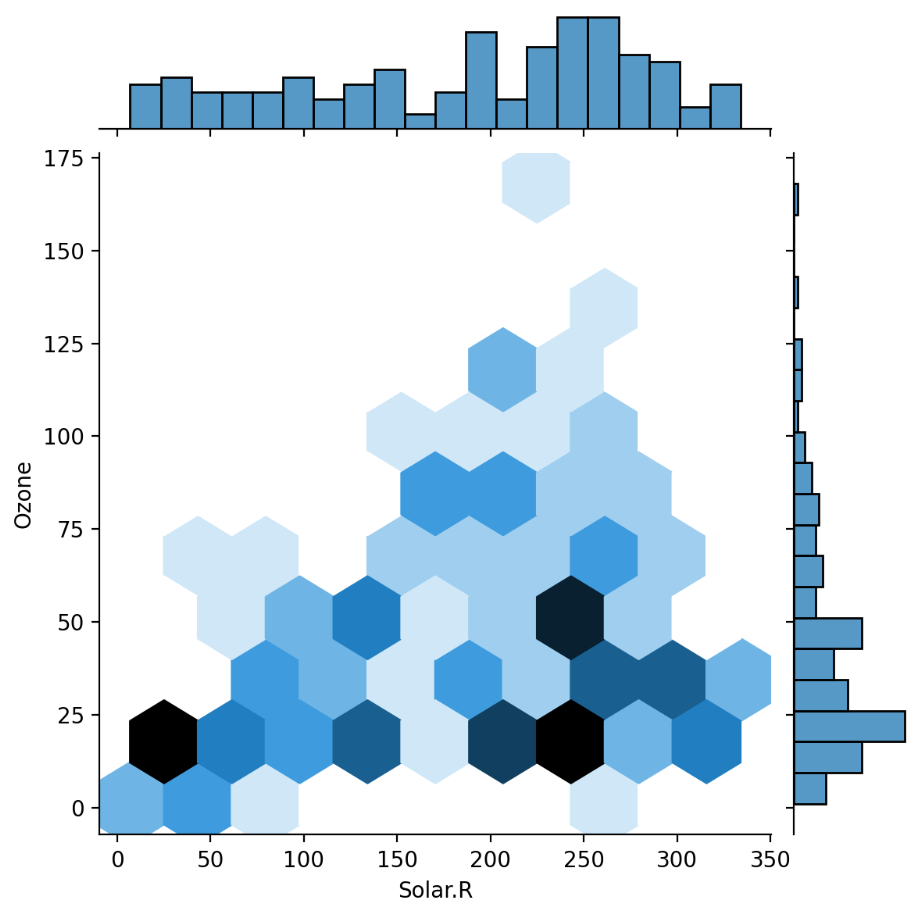

2. 수치화

수치형 변수와 수치형 변수의 관계를 비교하고자 할 때는 상관분석을 수행한다.
상관계수와 p-value를 사용하여 두 변수의 상관관계를 확인할 수 있다.

• 상관계수 r
  - 두 변수 간의 선형 관계의 강도와 방향을 측정하는 통계 지표이다.
  • -1 부터 1 사이의 값을 가진다.
  • 강함: 0.5 < |𝑟| ≤ 1
  • 중간: 0.2 < |𝑟| ≤ 0.5
  • 약함: 0.1 < |𝑟| ≤ 0.2
  • (거의)없음: |𝑟| ≤ 0.1
  • scipy.stats 라이브러리의 pearsonr() 함수로 상관관계를 확인한다.

result = **spst.pearsonr**(air['Temp'], air['Ozone'])

print(result)
print('* 상관계수:', result[0])
print('* p-value:', result[1])

pearsonr() 메서드의 결과값 중 첫번쨰 값이 상관계수가 되고, 두번째 값이 유의수준 p-value가 된다.

• 유의수준 p-value
  • 우리의 대립가설이 맞다고 받아드릴 때, 선택이 잘못될 확률을 의미한다.
  • 귀무 가설이 맞을 확률(대립가설이 틀릴 확률)과 동일하다.
    - 값이 매우 작을수록 좋다.
    - p-value는 대립가설이 받아들여질 때 실수일 확률이다.
  • 주의: 결측치가 있으면 계산되지 않습니다. 반드시 .notnull()로 제외하고 수행해야 한다.

대립가설(주장) : 두 수치형 변수가 상관관계가 있다.
귀무가설(일반적인 가설, 없어져야 하는 가설) : 두 수치형 변수가 상관관계가 없다.

air['Solar.R'].notnull()

notnull()은 null아 아닌것들이 True가 되고, null인 것들을 False가 된다.

air2 = air.loc[air['Solar.R'].notnull(), :]
result = spst.pearsonr(air2['Solar.R'], air2['Ozone'])

print(result)
print('* 상관계수:', result[0])
print('* p-value:', result[1])

loc[] 안에 넣어서 True인 것만 가져오도록 한다.

• Pandas의 corr() 메소드를 사용해서 변수들 간의 상관계수를 한번에 확인할 수 있다.

air.corr(numeric_only=True)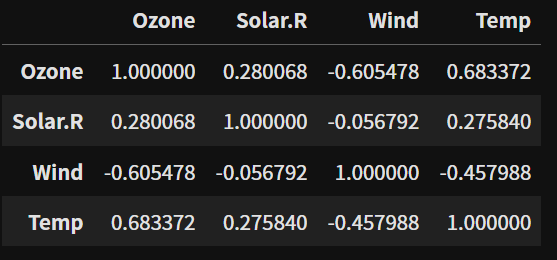

air.corr(numeric_only=True).style.background_gradient()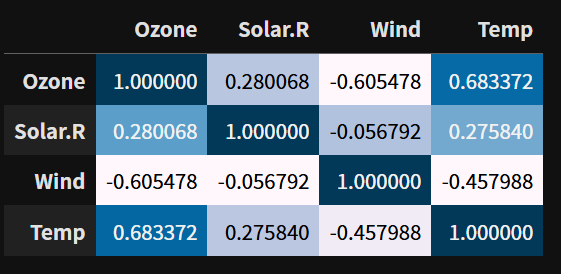

.style.background_gradient() 를 추가하여 heatmap과 유사하게 그래프를 그릴 수 있다.

• Seaborn의 heatmap() 함수로 상관계수를 시각화 할 수 있다.

plt.figure(figsize=(6, 6))
sns.heatmap(air.corr(numeric_only=True),
            annot=True,
            fmt='.3f',
            cmap='Blues',
            vmin=-1,
            vmax=1,
            square=True,
            cbar=False)
plt.show()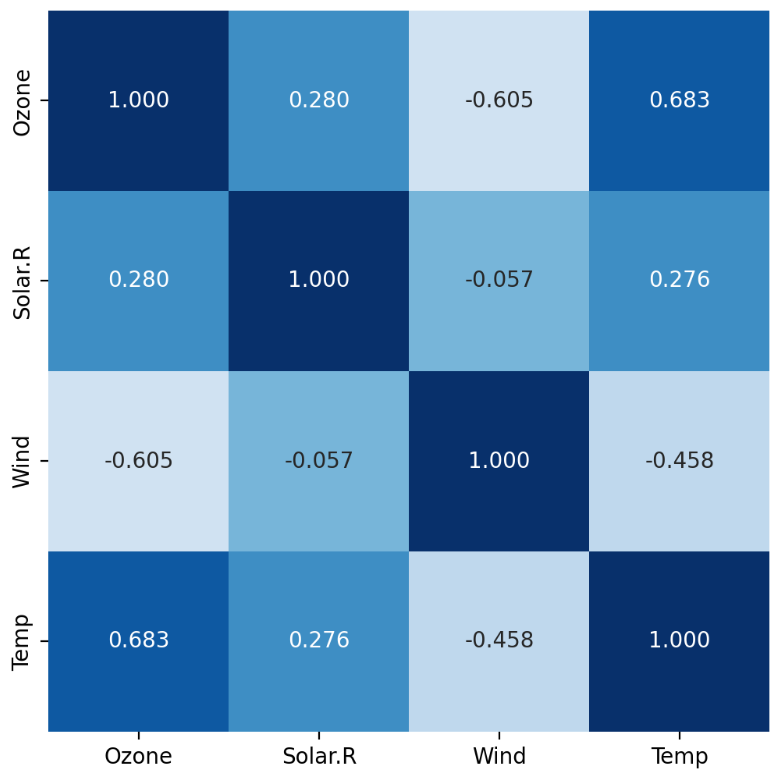

p-value는 상관관계가 있다 없다할 때 도움을 주는 값이다.
상관계수는 상관관계의 강함과 약함을 나타내는 값이다.

상관관계가 적은 값을 제거하라는 아니다.

3. 상관계수의 한계

상관계수는 방향이 아닌 폭을 의미한다. 상관계수가 0이더라도 의미를 가질 수 있다.

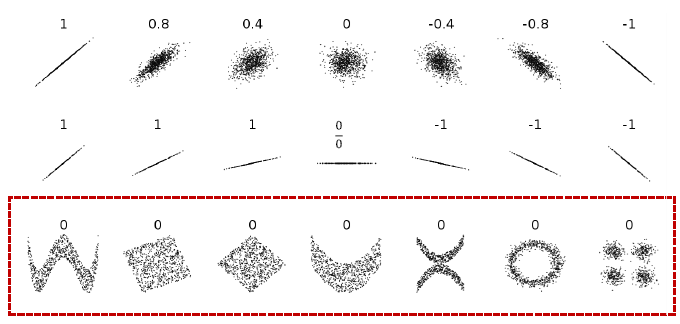
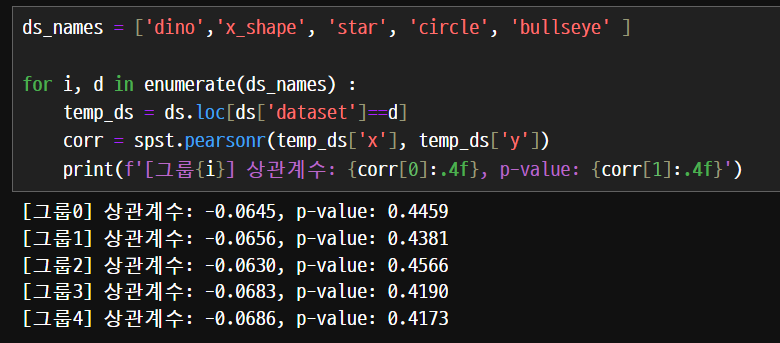
상관관계가 없다고 판단할 수 있다. 상관계수의 값이 매우 작고, p-value가 높은 값으로 상관관계가 없을 가능성이 높다.

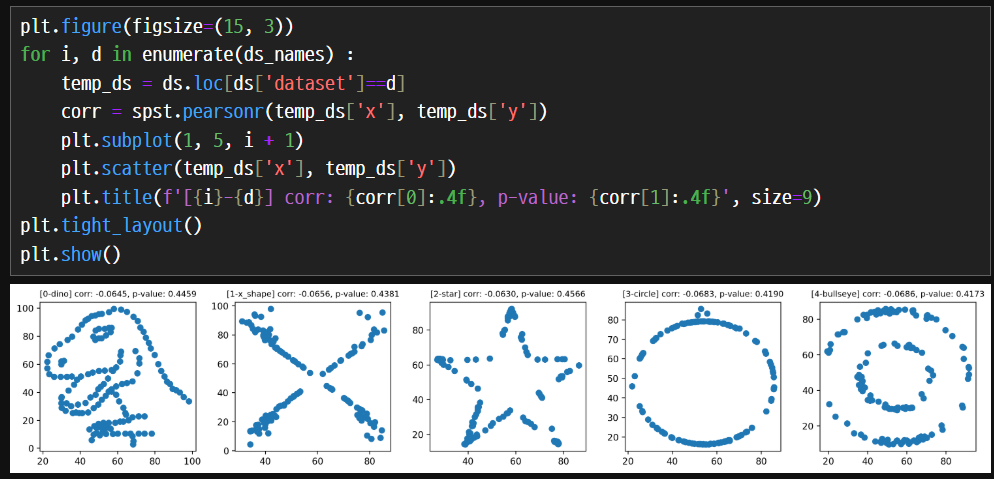
시각화를 해보면 패턴과 의미를 가진다. 수치화해서 하나의 숫자로 요약하는 데는 많은 장점이 있지만, 한계도 존재한다.

약한 상관관계는 상관관계가 없다와 같은 의미를 가진다.

07 가설과 가설검정

모집단(Population) : 대상 전체의 영역(미래의 데이터)
표본(sample) : 대상의 일부 영역(과거의 데이터)

가설은 모집단(Population)에 대한 가설 수립이다. 표본(sample)을 가지고 가설이 진짜 그러한지 검증한다.

고객의 이탈여부가 (y/n) 일 때 이탈여부(target)에 요인이 되는 값(x)을 뽑아서 초기 가설을 수립한다.

귀무가설 H_0 가 모두가 주장하는 바이다. (무로 돌아간다는 의미를 가진다. 없어졌으면 하는 가설)

• 현재의 가설
• 보수적인 입장
  대립가설 H_1 가 내가 주장하는 바이다. (연구를 통해서 밝혀내는 바이다.)
• 연구가설
• 새로운 가설

우리가 가지고 있는 데이터인 표본(sample)에 대해서 대립가설을 확인하고 모집단(Population)도 맞을 것이라고 주장한다.
• 대립가설: 매장지역(𝑥2)에 따라 수요량(𝑦)에 차이가 있다.
• 귀무가설: 매장지역(𝑥2)에 따라 수요량(𝑦)에 차이가 없다.
• 얼마나 큰 지, 얼마나 작은 지 또는 흔한 결과인지, 드문 결과인지 판단한다.

어느정도 차이에 따라서 차이가 크고 작다고 말할 것인가를 보면 상위와 하위의 각각 2.5%에 포함되면 차이가 있다고 판단한다.

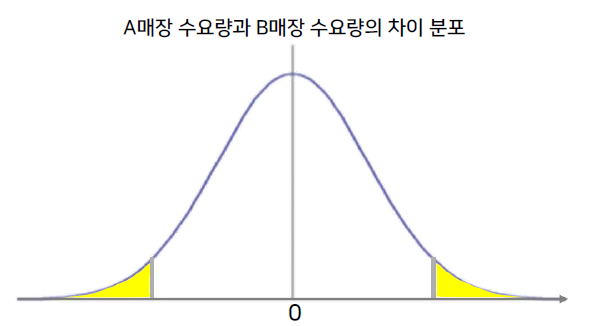
• 약 5%보다 작은 영역이면 차이가 크다고 할 수 있을 것임
• 대립가설이 맞다고 볼 수 있을 것임
• 이 면적의 의미는 대립가설이 맞다고 할 때 이 판단이 틀릴 확률

검정 통계량

가설을 입증하기 위해 검정통게량을 계산한다.

• t-통계량
• x^2(카이제곱)-통계량
• f-통계량

p-value의 값이 0.05보다 작으면 대립가설을 받아들인다. 다른 검정 통계량을 계산해 기준인 p-value
에 따라서 받아들일지 판단한다.

유의수준, 유의확률

대립가설이 맞다고 받아들일 때, 틀릴 확률과 5%를 비교한다.

• 5%보다 작다면 -> 대립가설을 채택한다.
• 5%보다 크다면 -> 귀무가설을 채택한다.

대립가설이 맞다고 받아들일 때 틀릴 확률이 유의확률, p-value이다.
유의수준 5%
• 5%: 피셔의 밀크티로 부터 유래
• 1%: 조금 더 보수적인 기준 (예: 의학, 제조 공정 분야)

08 과정 summary