01. review
상관계수의 절대값이 1에 가까울수록 상관관계가 크다.
p-value이 0.05보다 작을수록 상관관계가 있다. (귀무가설이 잘못되었고 우리가 주장하는 대립가설이 맞다)
02. 이변량 분석 ② - 범주형 → 수치형
Pclass별 age
Pclass별 Fare
Sex 별 Fare 평균을 구해서
02.1. 환경준비
import numpy as np
import pandas as pd
import random as rd
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.stats as spst
import warnings랜덤하게 추출할 떄 필요한 random 라이브러리도 가져온다.
고유한 티켓 번호는 삭제해준다. Cabin은 nan이 매우 많아서 컬럼을 삭제한다. name은 성별과 결혼 여부를 확인하는 부분만 남긴다.
02.2. 시각화
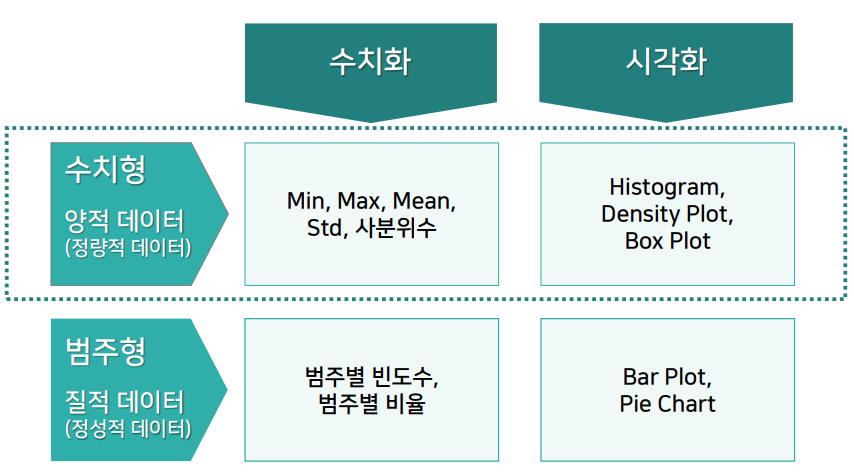
범주형 변수는 범주값 간의 개수와 범주값 간의 평균, 범주값 간의 값 분포를 시각화할 수 있다.
- Seaborn의 barplot() 함수는 범줏값 간의 평균을 비교해 표시합니다.
- Seaborn의 boxplot() 함수로 범줏값 간의 값 분포를 비교할 수 있습니다.
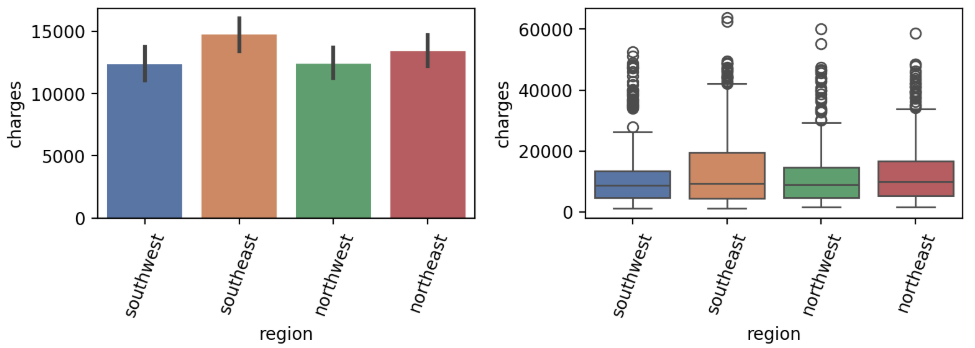
barplot은 자동으로 집계가 되어서 평균을 구해준다.
plt.figure(figsize=(8,3))
plt.subplot(1,2,1)
sns.barplot(x='region', y='charges', data=insurance, palette='deep')
plt.xticks(rotation=70)
plt.subplot(1,2,2)
sns.boxplot(x='region', y='charges', data=insurance, palette='deep')
plt.xticks(rotation=70)
plt.tight_layout()
plt.show()
02.3. 수치화
범주형 변수는 다음 두 가지 방법으로 수치화해 확인합니다.
- t-검정(두 범주)
- ANOVA(세 범주 이상)
1. t-검정
- 두 집단의 평균값이 서로 유의하게 다른지를 검정하는 통계적인 방법입니다.
- 데이터에 결측치가 있으면 계산이 안되니, notnull() 등으로 결측치를 제외한 데이터를 사용해야 합니다.
- scipy.stats 라이브러리의 ttest_ind() 함수로 t-검정을 수행합니다
자기의 이름을 숨기고 별칭을 만든다.
글자 하나를 부여한다.
p-value
t-value
f-vlaue
두 집단의 평균값에 차이가 있는지 확인한다.
표준편차는 개별값과 평균값의 차이를 의미한다. 표준편차가 크면 값들이 평균에서 멀리 위치한다. 평균 근처에 값들이 많으면 표준편차가 작다. (데이터의 분산을 보는 것과 유사)
표준오차는 전데 데이터인 모집단 안에 표본 데이터가 있다. 모집단 안에서 샘플링을 해서 데이터를 몇개 뽑아내 평균을 구한다. bootstrap(복원추출)을 통해 반복해서 구한 평균값들의 평균과 평균값들의 차이가 표준오차를 의미한다. 무작위 본원 추출을 통해서 뽑아낸 값들의 평균
📌 표준오차
- 모집단의 평균을 구하고 싶지만, 모집단이 너무 커서 구할 수 없습니다.
- 그래서 모집단에서 표본(Sample)을 뽑아 그 표본의 평균을 구합니다.
- 계속해서 표본을 뽑아 그 표본의 평균을 구합니다.
- 이 표본들의 평균의 평균이 모집단의 평균입니다.
- 그리고 이 표본들의 평균의 표준편차를 표준오차라고 부릅니다.
- 즉 추정값인 표본 평균들과 참값인 모평균과의 표준적인 차이라고 할 수 있습니다.
📌 t-statistics, t-통계량
- 두 집단 평균의 차이를 표준오차로 나눈 값입니다.
- 기본적으로는 두 평균의 차이로 이해해도 좋습니다.
- 우리의 가설(대립가설)은 차이가 있다는 것이므로, t-통계량 값이 크던지 작던지 하기를 바랍니다.
- 보통, t-통계량 값이 -2보다 작거나, 2보다 크면 차이가 있다고 봅니다.
📌 p-value
- t-검정에서 p-value는 유의확률(Significance Probability)로도 불립니다.
- 귀무가설(Null Hypothesis)을 검정할 때 사용되는 값입니다.
- p-value는 귀무가설이 맞을 때 표본에서 계산된 통계량이 나올 확률을 나타냅니다.
- 따라서, p-value가 작을수록 귀무가설이 틀릴 확률이 높아지므로, 귀무가설을 기각하게 됩니다.
- p-value 값이 작으면 통계적으로 유의미한 차이가 있다는 것을 의미한다고 보면 됩니다
s1 = rd.sample(pop1, 200)
s2 = rd.sample(pop1, 200)
t_test = spst.ttest_ind(s1, s2)
print('* t-statistic:', t_test[0])
print('* p-value:', t_test[1])
서로 같은 모딥단 pop1에서 뽑은 두개의 샘플 s1, s2 에 대해셔 ttest_ind를 통해서 t-value를 구해본다.
s1 = rd.sample(pop1, 200)
s2 = rd.sample(pop2, 200)
t_test = spst.ttest_ind(s1, s2)
print('* t-statistic:', t_test[0])
print('* p-value:', t_test[1])
서로 다른 모집단인 pop1과 pop2에서 각각 뽑은 두개의 샘플 s1, s2 에 대해셔 ttest_ind를 통해서 t-value를 구해본다. t-value는 절대값으로 확인하고, 평균의 차이가 매우 있다고 본다.
현재 대립가설은
p-value가 0.05보다 작으면 대립가설이 맞다는 것이고, 귀무가설이 틀리다.

p-value는 평균의 차이가 분명히 있다고 보임
t-statistic은 "두 평균의 차이"가 표준 오차 기준으로 얼마나 큰지를 나타내는 값이
t검증의 값만 보아도 절대값2보다 크면
2. ANOVA
집단이 3개이상일 때 차이가 있는지 없는지 확인한다.
- 세 개 이상의 집단 간 차이는 분산분석(ANOVA)으로 비교합니다.
- ANOVA: ANalysis Of VAriance
- 여기서 기준은 전체 평균 입니다.
- scipy.stats 라이브러리의 f_oneway() 함수로 분산분석을 수행합니다.
집단 간 분산 / 집단 내 분산
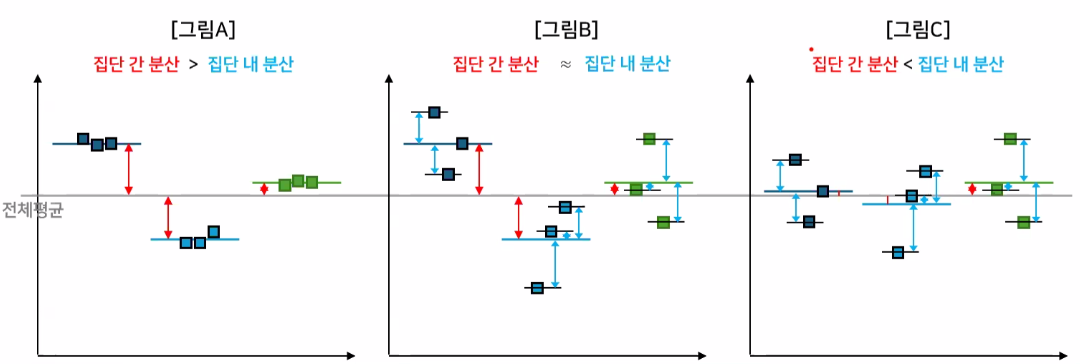
📌 f-statistics, f-통계량, f-value
- 두 개 이상의 집단 간 분산의 비율을 검정하는 데 사용되는 통계량입니다.
- 분산분석(ANOVA)에서 사용되며, 각 집단 내에서의 분산과 각 집단 간의 분산의 비율을 계산합니다.
- $f-통계량=\frac{집단간 분산}{집단내 분산} $
- 이 계산 결과로 각 집단이 모집단으로부터 동일한 분산을 가지는지를 검정합니다.
- 분산의 비율이 작을수록 1에 가까운 값을 가집니다.
- 분산의 비율이 클수록 f-통계량 값이 커집니다.
- f-통계량 값이 크다는 것은 각 집단 간 차이가 통계적으로 유의미하다는 것을 나타냅니다.
- 보통, f-통계량 값이 2~3 이상이면 차이가 있다고 봅니다.
temp = titanic.loc[titanic['Age'].notnull()]
p1 = temp.loc[temp['Pclass']==1, 'Age']
p2 = temp.loc[temp['Pclass']==2, 'Age']
p3 = temp.loc[temp['Pclass']==3, 'Age']
anova = spst.f_oneway(p1, p2, p3)
print('* f-statistic:', anova[0])
print('* p-value:', anova[1])
p-value는 -10^24로 0.05보다 매우 작기에 평균의 차이가 있다고 해석한다.
t-value는 2나 3보다 크기 때문에 평균의 차이가 있다고 해석한다.
temp = titanic.loc[titanic['Fare'].notnull()]
s = temp.loc[titanic['Embarked']=='S', 'Fare']
q = temp.loc[titanic['Embarked']=='Q', 'Fare']
c = temp.loc[titanic['Embarked']=='C', 'Fare']
anova = spst.f_oneway(s, q, c)
print('* f-statistic:', anova[0])
print('* p-value:', anova[1])
r1 = insurance.loc[insurance['region']=='southwest', 'charges']
r2 = insurance.loc[insurance['region']=='southeast', 'charges']
r3 = insurance.loc[insurance['region']=='northwest', 'charges']
r4 = insurance.loc[insurance['region']=='northeast', 'charges']
anova = spst.f_oneway(r1,r2,r3,r4)
print('* f-statistic:', anova[0])
print('* p-value:', anova[1])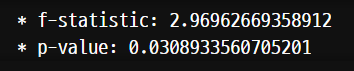
실습
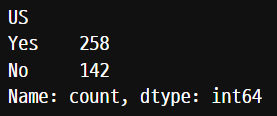
국내외 여부(US) → 판매량(Sales)
carseat['US'].value_counts() 를 통해서 컬럼의 범주값의 이름을 확인한다.
yes = carseat.loc[carseat['US']=='Yes', 'Sales']
no = carseat.loc[carseat['US']=='No', 'Sales']
t_test = spst.ttest_ind(yes, no)
print('* t-statistic:', t_test[0])
print('* p-value:', t_test[1])
p-value 가 0.05보다 낮음으로 귀무가설이 틀렸고 대립가설이 맞다.
그럼으로 대립가설인 두 평균의 차이가 있다고 본다.

300에서 299개는 어떤 것이 되어도 상관없지만 마지막 1개는 자유도가 없음.. 그럼으로 자유도는 299라고 구한다.
- df는 자유도를 의미한다.
- df는 전체값에 대해서 자유도를 구한다.
- 범주값이 2개임으로 (전체값-2)로 자유도를 구할 수 있다.
carseat['ShelveLoc'].value_counts()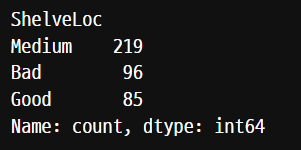
value_counts()를 통해서 범주형 변수의 범주값의 개수를 확인한다 .
m = carseat.loc[carseat['ShelveLoc']=='Medium', 'Sales']
b = carseat.loc[carseat['ShelveLoc']=='Bad', 'Sales']
g = carseat.loc[carseat['ShelveLoc']=='Good', 'Sales']
anova = spst.f_oneway(m,b,g)
print('* t-statistic:', anova[0])
print('* p-value:', anova[1])
t-value는 두 평균의 차이를 나타낸다. 절댓값 2보다 큼으로 두 평균의 차이가 있다고 해석한다.
03. 이변량 분석 ③ - 범주형 → 범주형
Sex나 Pclass와 Survived가 관련이 있을까? 에 대해서 알아본다.
03.1. 환경준비
import numpy as np
import pandas as pd
import random as rd
import matplotlib.pyplot as plt
import seaborn as sns
from statsmodels.graphics.mosaicplot import mosaic
import scipy.stats as spst
import warningsfrom statsmodels.graphics.mosaicplot import mosaic 시각화를 위해 필요한 라이브러리를 추가한다.
03.2. 교차표
범주값의 수치화 비교는 범주값의 비율을 통해서 확인한다.
- 범주 vs 범주 를 비교하기 위해서는 Pandas의 crosstab() 함수를 사용해 교차표를 먼저 만들어야 합니다.
- Sex → Survived 관계를 비교하기 위해 교차표를 만들어봅니다.
- noramlize 매개변수에 따라서 범주값의 비율을 행의 합, 열의 합, 전체의 합으로 다르게 표현할 수 있다.
pd.crosstab(titanic['Sex'], titanic['Survived'])crosstab() 메서도를 이용해서 교차표를 빠르게 그릴 수 있다.
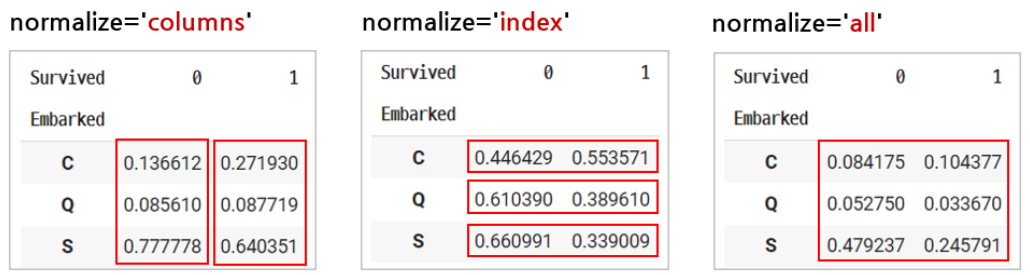
- index를 많이 사용한다.
03.3 시각화
1) 100% Stacked Bar
누적바를 의미한다.
- 우선 normalize='index' 를 설정한 교차표를 작성합니다.
- Pclass 변수가 세 개의 범줏값을 가지므로 세 개의 행이 생깁니다.
- normalize='index'를 지정했으므로 각 행의 합은 1이 됩니다.
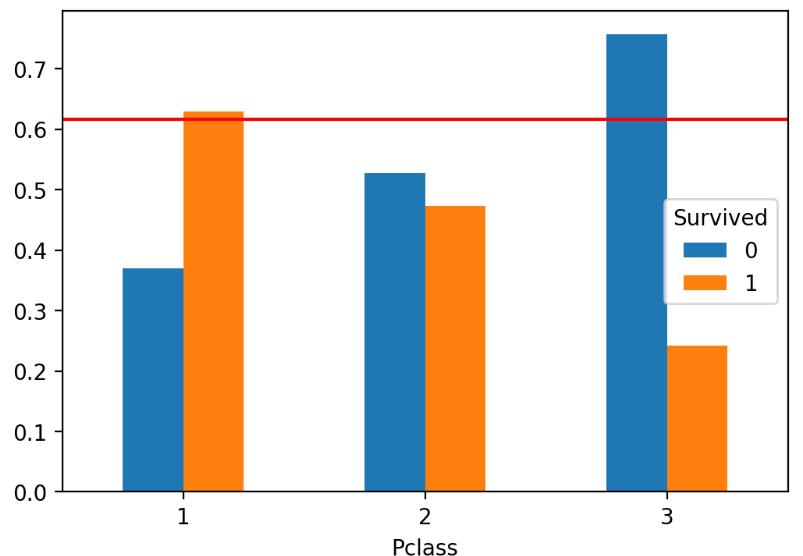
매개변수 stacked=True를 통해서 stacked bar를 그릴 수 있다.
table.plot(kind='bar', stacked=True)
plt.axhline(1-titanic['Survived'].mean(), color='r')
plt.xticks(rotation=0)
plt.show()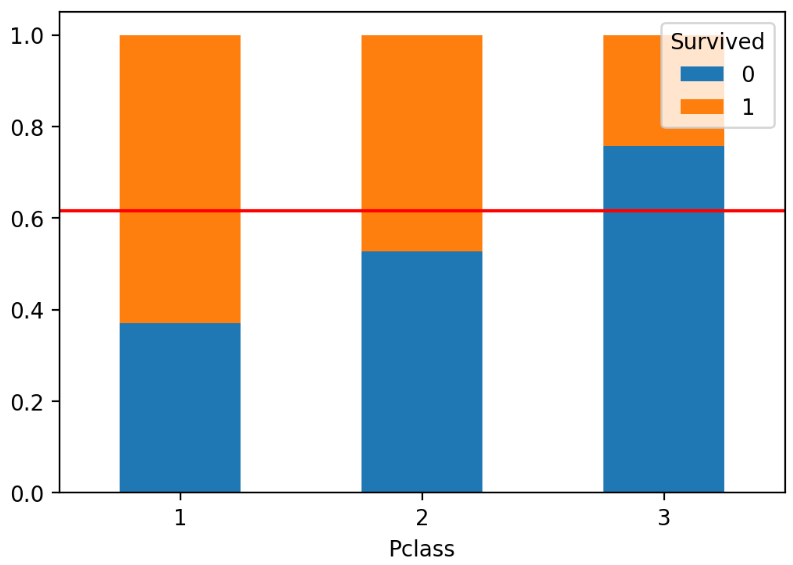
교차표 table를 통해서 plot() 메소드로 그래프를 그릴 때, normalize=index 를 설정하여 행의 합이 1이 되도록 설정하여 stacked bar를 그렸을 때 모두 합이 1인 그래프를 그릴 수 있다.
0과 1로 구성된 값의 평균은 율을 의미힌다.
1,1,1,0,0 과 같을 때 생존1, 사망0이면 생존율을 평균값과 같다.
이때 사망률은 1-생존율을 통해서 구할 수 있다.
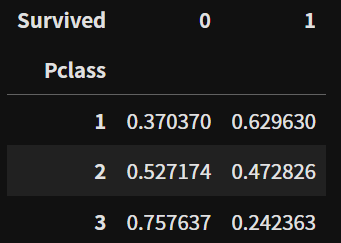
table = pd.crosstab(titanic['Embarked'], titanic['Survived'], normalize='index')
display(table)
table.plot(kind='bar', stacked=True)
plt.axhline(1-titanic['Survived'].mean(), color='r')
plt.xticks(rotation=0)
plt.show()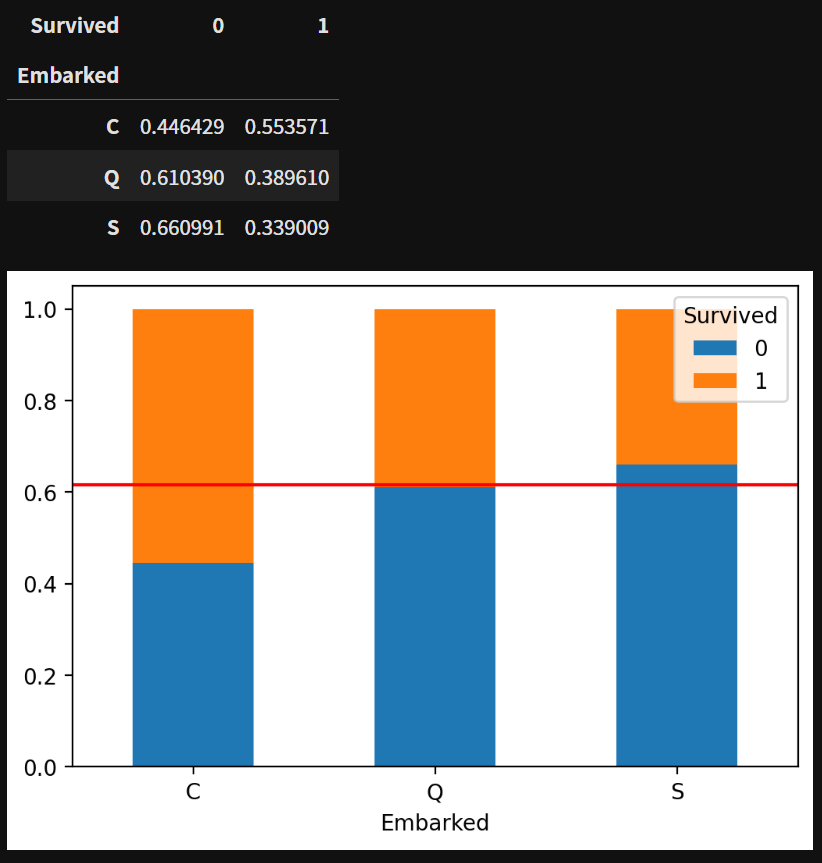
stacked bar는 몇명인지 정확히 알 수 없는 것이 단점이다. 이 때문에 mosaic bar가 생김
2) Mosaic Bar
stacked bar의 양에 대한 비교가 어려움 점을 보완하여 mosaic bar를 사용한다.
- 100% Stacked Bar는 비율만 비교하므로 양에 대한 비교는 할 수 없습니다.
- Mosaic Plot으로 양에 대한 비교를 해봅니다.
- tatsmodels.graphics.mosaicplot의 mosaic() 함수로 Mosaic Plot을 그립니다.
데이터를 넣을 때 정렬을 해서 넣으면 클래스를 정렬하여 그릴 수 있다.
mosaic(titanic.sort_values(['Pclass', 'Survived']), ['Pclass', 'Survived'], gap=0.01)
plt.axhline(1-titanic['Survived'].mean(), color='r')
plt.show()- sort_values() 메소드를 사용해 원하는 순서로 정렬해 표시할 수 있습니다.
- gap 옵션으로 영역들 사이 간격을 조정할 수 있습니다.
mosaic(titanic, ['Title', 'Survived'], label_rotation=(90,0))
plt.tight_layout()
plt.show()일반적인 귀무가설이 참인 경우에는 아래 그래프를 따른다. 이 그림에서 벗어난 경우가 차이가 있다라고 분석한다.
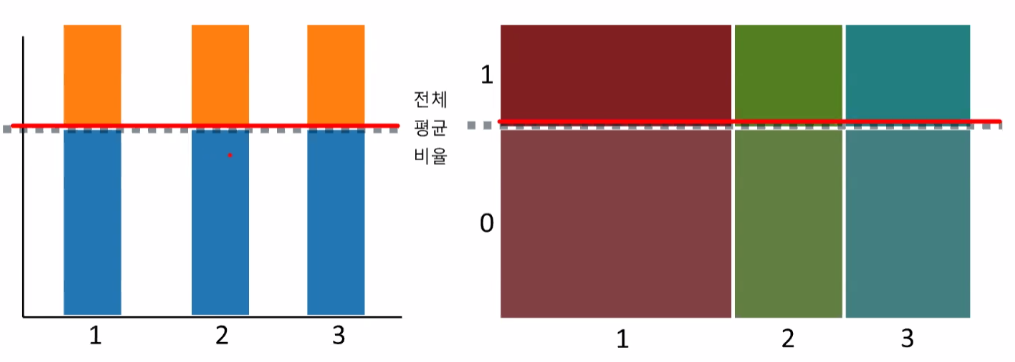
crosstab, 교차표
100% stacked bar 행의 합이 1이 되는 교차표를 기준으로 그린다.
mosaic 영역의 크기로 데이터를 예측
03.4. 수치화
카이제곱검정(chi-squared test)
- 범주형 → 범주형 관계를 수치와해 비교할 때는 카이제곱검정(Chi-Squared Test) 을 사용합니다.
- scipy.stats 라이브러리의 chi2_contingency() 함수로 카이제곱검정을 수행합니다.
- 카이제곱검정은 검정으로도 불립니다.

카이제곱은
observd
expected 기대값
- 카이제곱통계량은 자유도의 2-3배 보다 크면, 차이가 있다고 본다.
- 범주형 변수의 자유도는 (범주의 수-1)로 구한다.
- x 변수의 자유도 × y 변수의 자유도
- 두범주형 변수에 대해서 normalize 매개변수를 주지 않고 교차표 crosstab을 만든다.
- chi2_contingency() 메서드에 만든 교차표를 넣어서 구한다.
기대빈도의 공식에따라 기대빈도를 계산해 관계가 없음을 의미한다.

실제 기대빈도에 따라서 카이제곱이 계산된다. 기대빈도가 저렇게 계산되는 이유는 귀무가설에서 행과 열이 서로 독립적이라고 가정하기 때문이다.
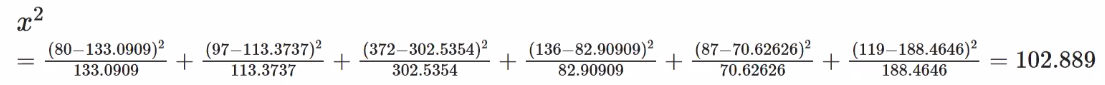
자유도에 따라서 카이제곱통계량의 의미를 분석한다.
2x1=2 2의 2에서 3배인 4-6 보다 크면 차이가 있다고 보고, 결과값인 102와 비교해 차이가 있음을 나타낸다.
p-value는 0.05보다 작음으로 대립가설이 채택된다. 현재 대립가설은 범주값이 관련이 있다/차이가 있다를 의미한다.
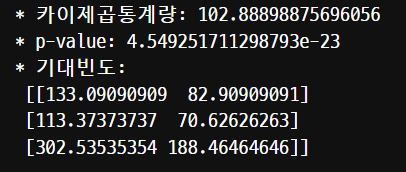
table = pd.crosstab(titanic['Embarked'], titanic['Survived'])
print(table)
print('-' * 20)
result = spst.chi2_contingency(table)
print(' * 카이제곱통계량:', result[0])
print(' * p-value:', result[1])
print(' * 기대빈도:', result[3])
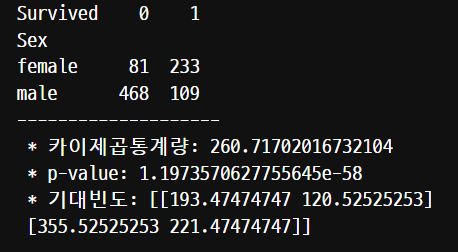
카이제곱통계량은 자유도인 2에 대해서 4-6보다 큰 값이 나오는 것으로 관련이 있음을 나타낸다.
p-value 는 0.05보다 작음으로 대립가설인 범주형 변수들이 관련이 있다가 채택된다.
pvalue가 0.05보다 크면 두 값의 차이가 통계량만큼 관련이 있다.
카이제곱통계량이 3.6이고, p-value이 0.3일 때의 경우)
자유도2에 대해서 4-6보다 작기 때문에 연관성이 없다고 볼 수 있는데, p-value가 0.05보다 작지 않아 우리의 대립가설인 '두 범주형 변수간의 연관이 있다'에 대해서 기각해야 한다.
카이제곱통계량의 분석을 p-value로 확정한다고 생각한다. p-value를 마지막 결정값이라고 본다.
카이제곱통계량의 분석에서 2-3배보다 커서 연관성이 있다고 나왔지만, p-value에서의 값이 커서 대립가설을 기각할 수도 있다.
target값에 대해서 어떤 컬럼이 관련이 있다는 결과가 나왔다면?
어떤 컬럼이라는 인사이트를 비즈니스에 연결해야 한다.
카이제곱통계량은 실제값에서 얼마나 벗어났는가에 대한 강도를 나타내는 값으로 카이제곱통계량이 100과 200에 대해서 200이 100에 대해서 2배 큰것이 아님. 그냥 두 범주형 변수가 연관성이 있는지만 판단한다. 카이제곱은 표본 크기에 영향이 커서 높은 카이제곱 값이 반드시 강한 연관성이 있다고 말할 수는 없다.
범주형-범주형 변수는
수치화는 카이제곱통계량
시각화는 bar plot과 mosaic plot
실습
1️⃣ 성별(Gender) → 이직 여부(Attrition)
table_gen = pd.crosstab(data['Gender'], data['Attrition'], normalize='index')
display(table_gen)
table_gen.plot(kind='bar', stacked=True)
plt.axhline(1-data['Attrition'].mean(), color='r')
plt.show()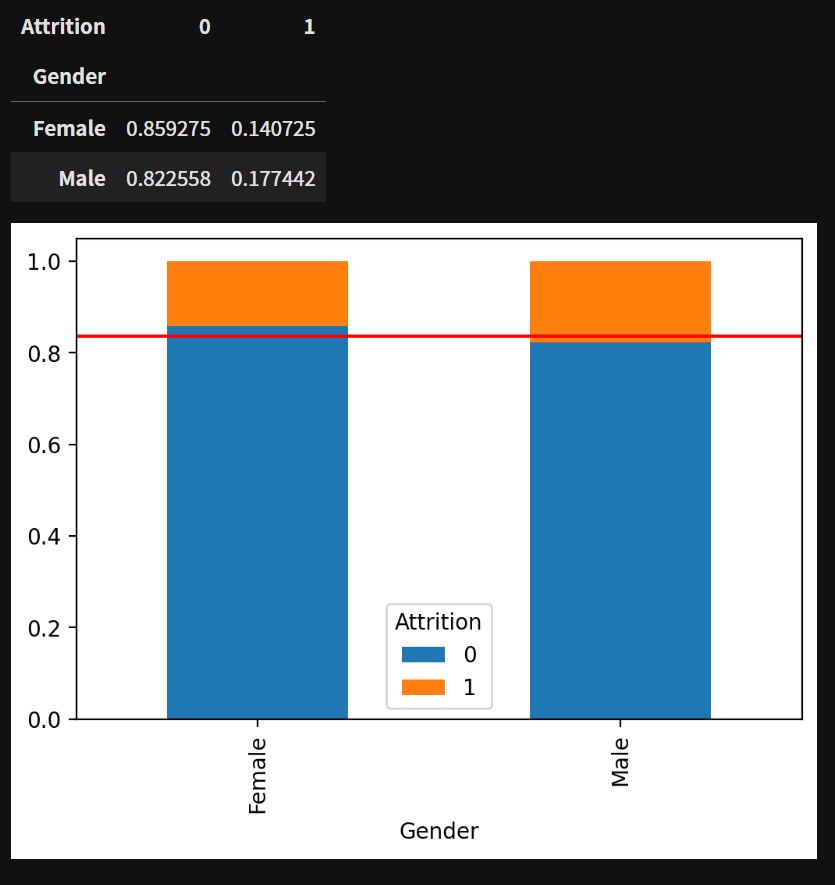
table_gen = pd.crosstab(data['Gender'], data['Attrition'])
print(table_gen)
result = spst.chi2_contingency(table_gen)
print(' * 카이제곱통계량:', result[0])
print(' * p-value:', result[1])
print(' * 기대빈도:', result[3])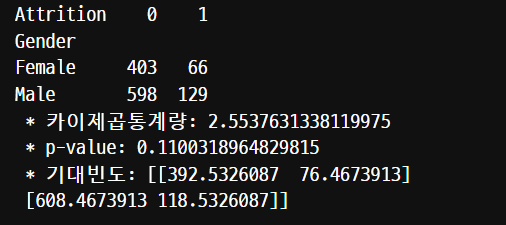
카이제곱통계량은 자유도인 2에 대해서 4-6보다 작기 때문에 연관이 없다고 해석한다.
p-value의 값이 0.05보다 큼으로 대립가설(두 범주형 변수가 연관이 있다)를 기각한다.
3️⃣ 결혼 상태(MaritalStatus) → 이직 여부(Attrition)
table_mar = pd.crosstab(data['MaritalStatus'], data['Attrition'], normalize='index')
display(table_mar)
table_gen.plot(kind='bar', stacked=True)
plt.axhline(1-data['Attrition'].mean(), color='r')
plt.show()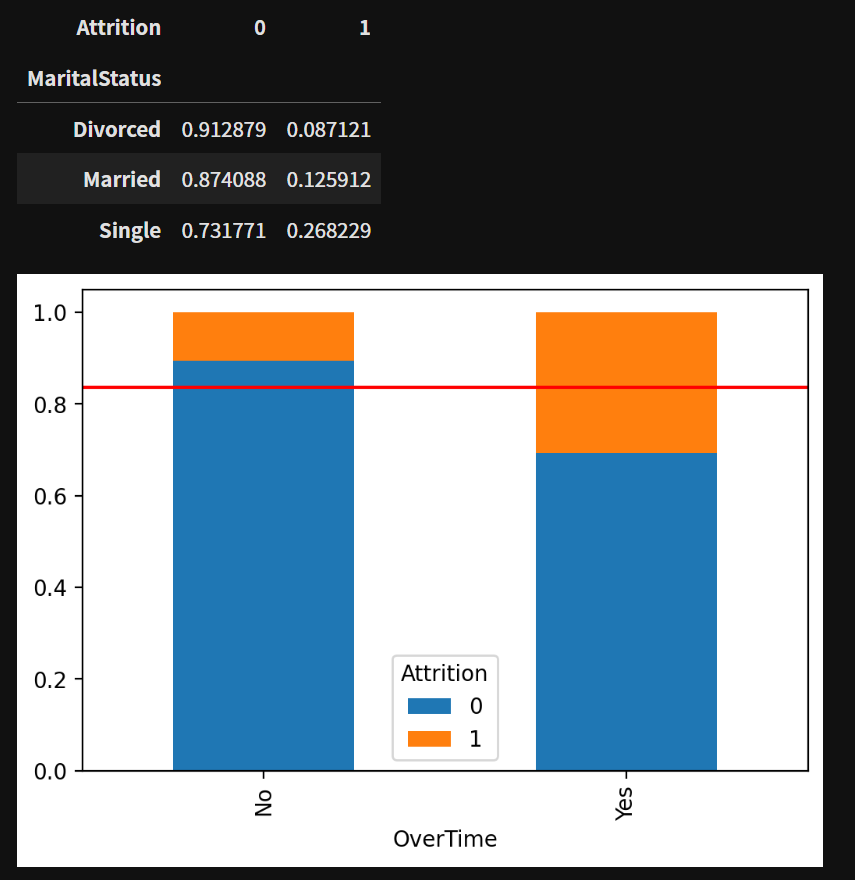
table_mar = pd.crosstab(data['MaritalStatus'], data['Attrition'])
print(table_mar)
result = spst.chi2_contingency(table_mar)
print(' * 카이제곱통계량:', result[0])
print(' * p-value:', result[1])
print(' * 기대빈도:', result[3])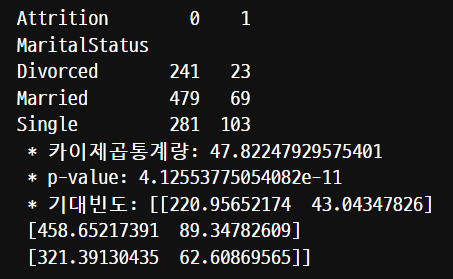
카이제곱통계량은 자유도인 2에 대해서 4-6보다 크기 때문에 연관이 있다고 해석한다.
p-value의 값이 0.05보다 작음으로 대립가설(두 범주형 변수가 연관이 있다)를 채택한다.
함수를 이용해서 한번에 할 수 있다.
vars = ['Gender','JobSatisfaction','MaritalStatus','OverTime']
for v in vars:
table = pd.crosstab(data[v], data['Attrition'])
result = spst.chi2_contingency(table)
print('*', v )
print(' * 카이제곱통계량:', result[0])
print(' * p-value:', result[1])
print(' * dof(자유도):', result[2])
print(' * 기대빈도:', result[3])
print('-' * 30)04. 이변량 분석 ④ - 수치형 → 범주형
수치화애서 분석하는 것은 큰 의미는 없지만 시각화에 대해서 의미가 크다.
범주형 변수인 survived에 대해서 수치형 변수인 age를 파악해보자
04.1. 환경준비
import pandas as pd
import numpy as np
import random as rd
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
import warnings04.2. 시각화
수치형 변수와 범주형 변수의 시각화는 histogram과 Density plot
1) histogram의 hue 매개변수
- Seaborn의 histplot() 함수로 Histogram을 그립니다.
- Histogram을 사용해 Age 변수의 값 분포를 Survived 변수를 기준으로 나눠서 표시해 봅니다.
sns.histplot(x='Age', hue='Survived', data=titanic, bins=20)
plt.show()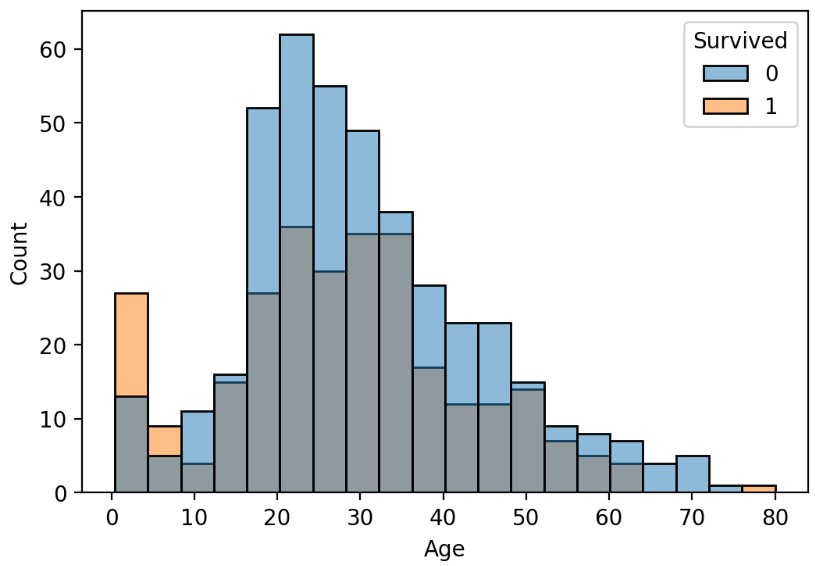
sns의 hue 매개변수를 사용하여 수치형 변수와 범주형 변수를 분석한다.
2) Density Plot의 hue 매개변수
- Seaborn의 kdeplot() 함수로 Density Plot을 그립니다.
sns.kdeplot(x='Age', hue='Survived', data=titanic)
plt.show()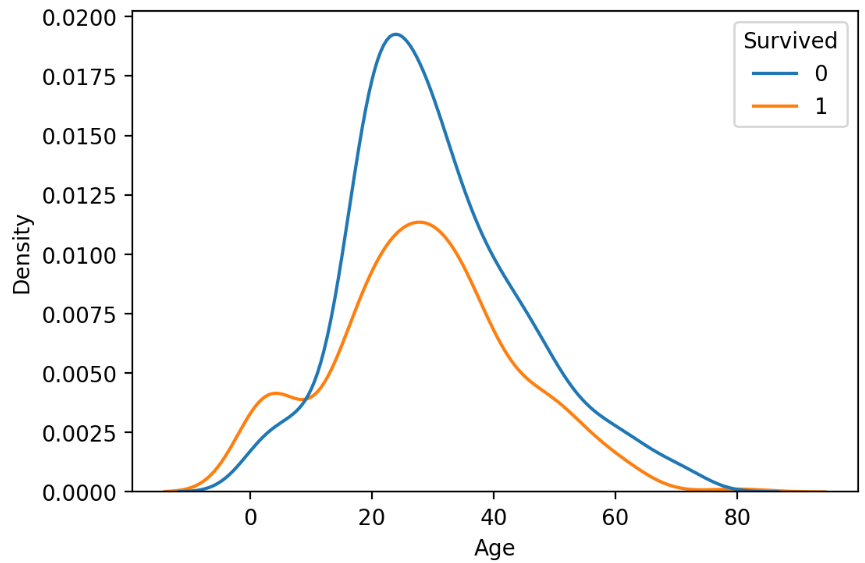
sns의 hue 매개변수를 사용하여 수치형 변수와 범주형 변수를 분석한다. 두 그래프의 아래 면적의 합이 1이 된다. (defult)
common_norm=False 로 설정하면 개별 그래프의 면적이 각각 1이 된다.
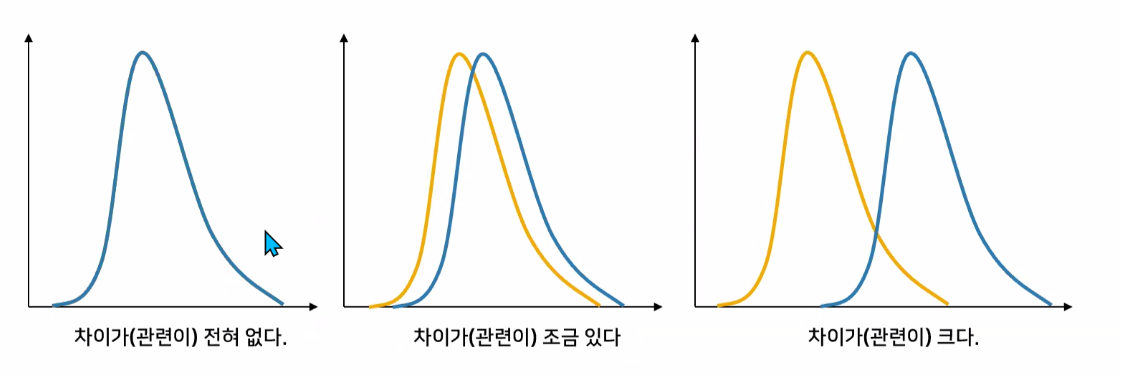
함수가 겹칠수록 차이가 없다 = 관련이 없다 를 보여준다.
3) multiple='fill' 지정
- multiple 매개변수 값을 'fill' 로 지정해 비율을 비교할 수 있습니다.
- 단, 양의 비교가 아닌 비율을 비교합니다.
sns.kdeplot(x='Age', hue='Survived', data=titanic, multiple='fill')
plt.axhline(titanic['Survived'].mean(), color='r')
plt.show()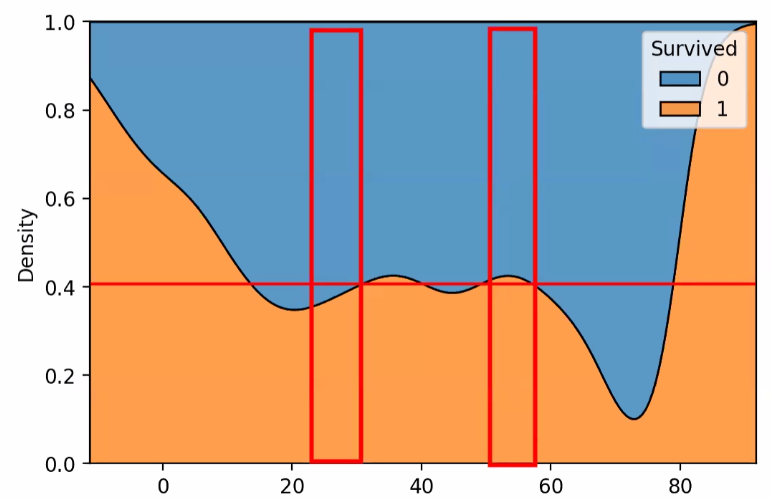
생존율을 붉은 선으로 그려준다. 1의 값이 아래로 깔렸기 때문에 1-생존율을 사용하지 않아도 된다.
전체적인 분포를 보여주기 위해 약간의 왜곡이 발생한다. (실제 데이터에서는 80세가 1명이지만 부드러운 곡선을 그리기 위해 왜곡이 발생한다) 분석할 때는 일정구간을 보고 범주형 변수에 대해서 해석한다 .
histplot를 이용해서 그리면 데이터가 없는 영역도 보여준다.
sns.histplot(x='Fare', hue='Survived', data=titanic, bins=20, multiple='fill')
plt.axhline(titanic['Survived'].mean(), color='r')
plt.show()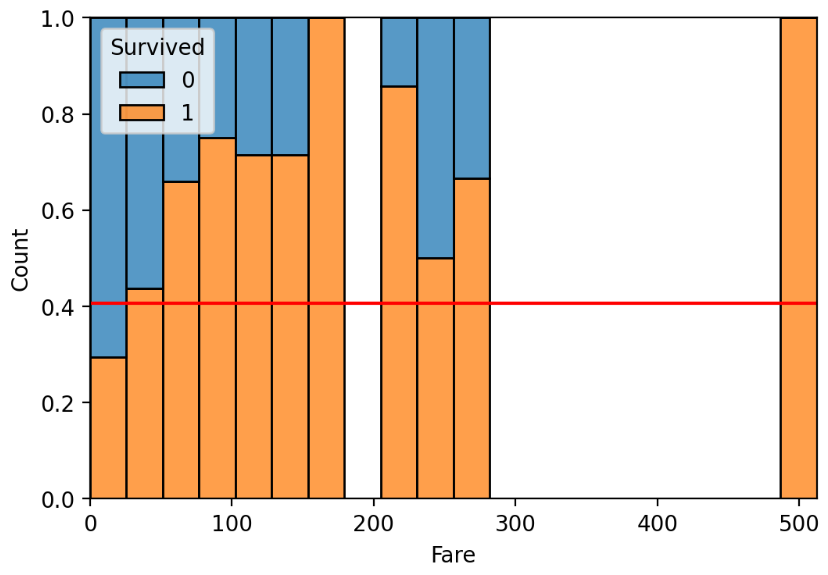
subplot으로 한번에 그린다.
target='ADMIT'
plt.subplot(1,3,1)
sns.histplot(x='TOEFL', hue='ADMIT', data=admission)
plt.subplot(1,3,2)
sns.kdeplot(x='TOEFL', hue='ADMIT', data=admission)
plt.subplot(1,3,3)
sns.kdeplot(x='TOEFL', hue='ADMIT', data=admission, multiple='fill')
plt.axhline(admission[target].mean(), color='r')
plt.tight_layout()
plt.show()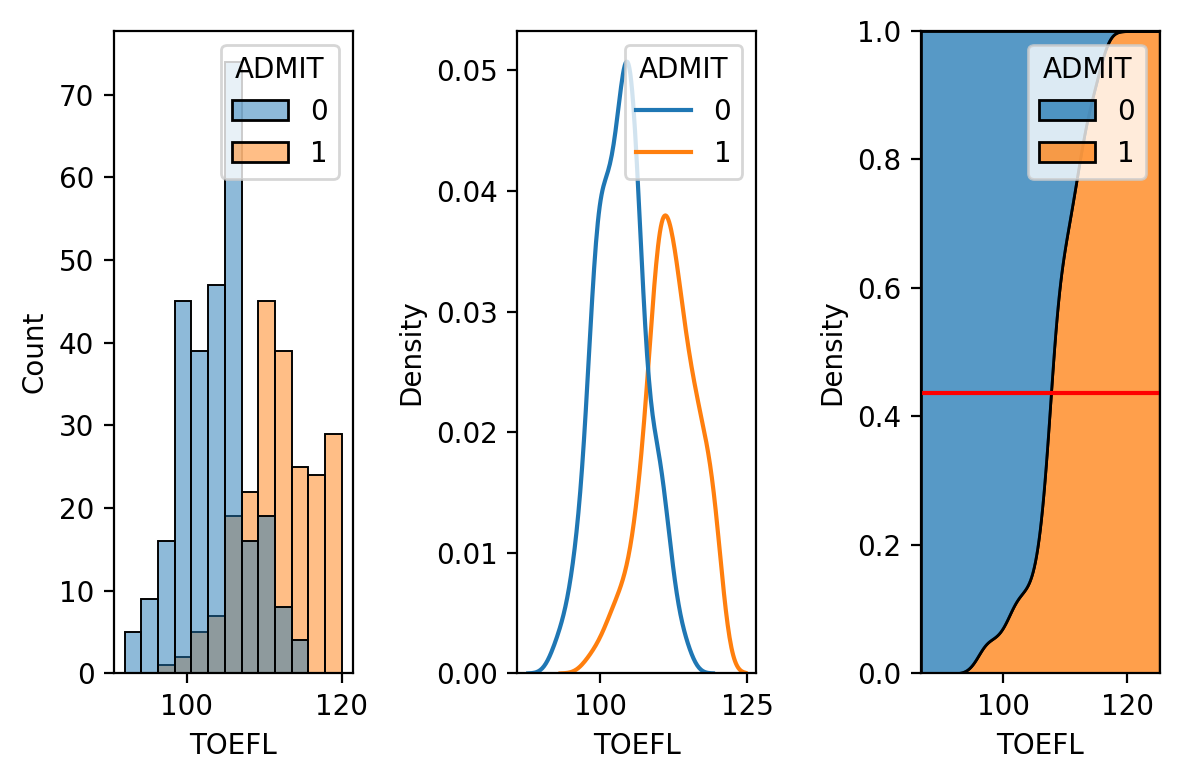
04.2. 수치화
- 숫자 vs 범주에 대해 딱 맞는 가설검정 도구가 없으므로, 로지스틱 회귀모델로 부터 p-value를 구해봅니다.
머신러닝은 x변수들을 이용해서 target값을 맞추는 것이다.
로지스틱 회귀모델은 하나의 x에 대해서 target을 예측하도록 하는 것이다. 예측하는 과정에서 p-value를 구할 수 있다.
model = sm.Logit(titanic['Survived'], titanic['Age'])
result = model.fit()
print(result.pvalues)sm.Logit(endog, exog)로 endog은 응답 vaiable이다.
Logit(taregt, x변수) 순서로 작성해주어 x변수에 대해서 target값을 예측한다.
print(result.summary()) 으로 아래와 같은 통계값에서 확인할 수 있다.
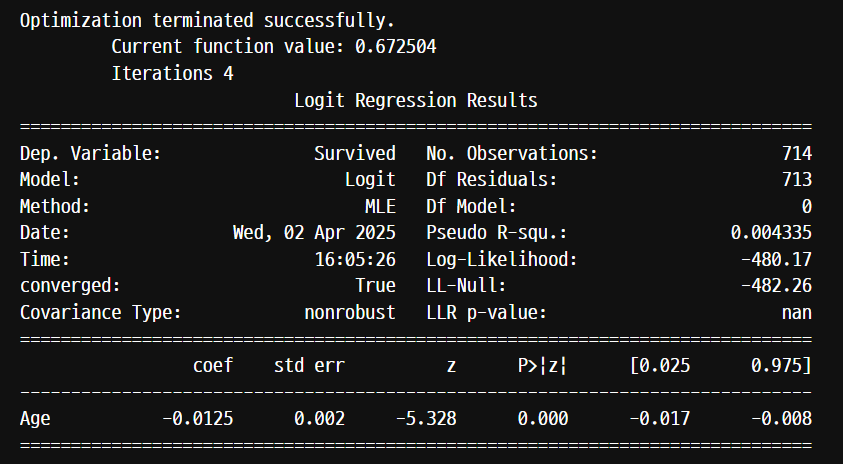
model = sm.Logit(titanic['Survived'], titanic['Parch'])
result = model.fit()
print(result.pvalues)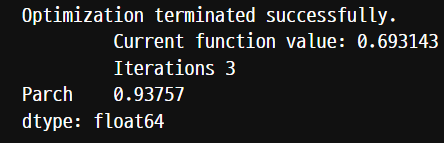
p-value의 값이 0.05보다 값이 큼으로 Parch와 Survived는 거의 관계가 없음을 의미한다. 대립가설이 기각된다.
실습
model = sm.Logit(attrition['Attrition'], attrition['TotalWorkingYears'])
result = model.fit()
print(result.pvalues)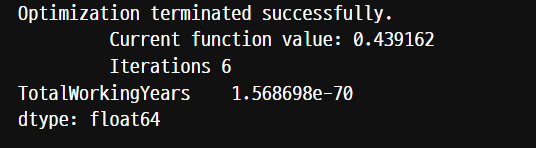
p-value의 값이 0.05보다 작음으로 대립가설이 채택된다.
대립가설은 수치형변수와 범주형 변수 사이의 연관이 있다
아래처럼 순서를 바꿔서 입력하면 오류가 발생한다.
target변수는 이진값이 되어야 한다.
model = sm.Logit(attrition['TotalWorkingYears'], attrition['Attrition'])
result = model.fit()
print(result.pvalues)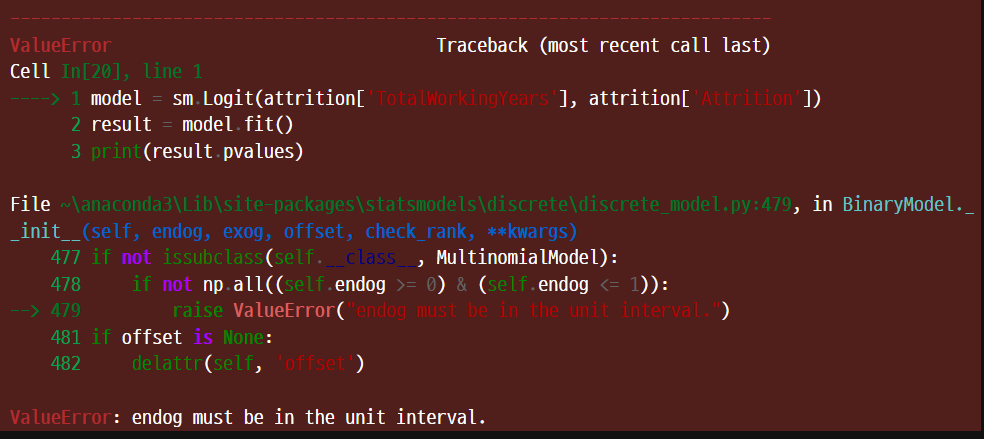
t-value의 통계량이 자유도 2~3배 범위에 포함된다면 관련성이 없다. 이후의 p-value로 확정짓는다.
정리
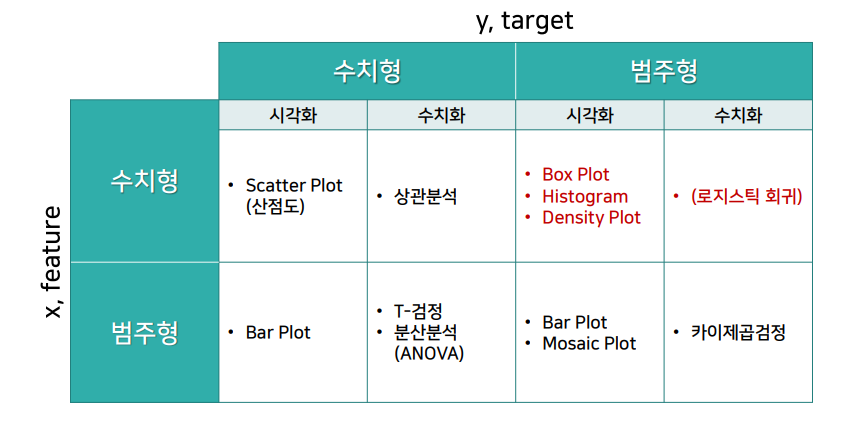
추가
jupyter lite
chrome 창에서 jupyter lite를 사용하면 anaconda의 jupyter lab과 동일하게 사용할 수 있다.
기존의 로컬에 있던 폴더를 드래그 앤 드롭으로 넣을 수 있다.
- anaconda에 오류가 발생한 경우
- anaconda가 설치되지 않은 경우
- 시간이 좀 지나면 파일이 사라져버린다
구글 드라이브에서 새 폴더를 만들어서 실행할 파일을 넣고, 파일을 colab으로 열면됨
설정해주면 된다.