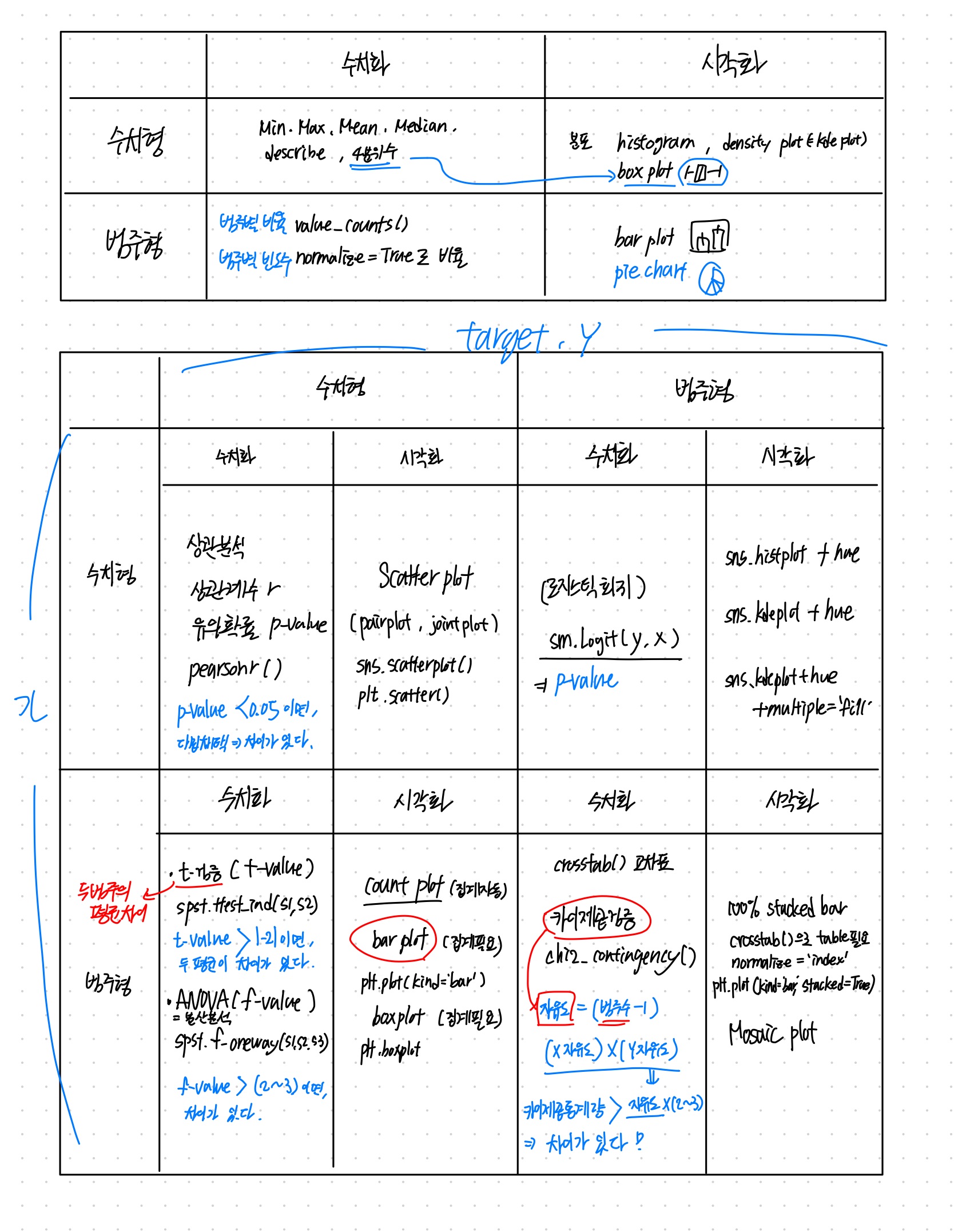
차이가 있다는 것은 관련이 있다는 것과 같은 의미이다.
수치형 -> 수치형
x 수치형과 y 수치형 간의 관계를 분석할 때, 상관계수 r (-1 ~ 1)과 유의확률 p-value를 떠올린다. spst.pearsonr()을 통해서 모두 구할 수 있다.
상관계수는 0에 가까울수록 관련이 없다.
상관계수는 -1과 가까울수록 관련이 있다.(음의 강한 상관관계)
상관계수는 1과 가까울수록 관련이 있다.(양의 강한 상관관계)
- 귀무가설: 상관계수가 0이다.
- 대립가설: 상관계수가 0이 아니다.
범주형 -> 수치형
x 범주형과 y 수치형 간의 관계를 분석할 때, 범주값별로 나누고 샘플링을 떠올리면서 두 범주의 평균 차이를 나타내는 t-검증을 기억한다.
t-value > 절대값|-2| 이면, 차이가 있다.
- 귀무가설: 객실 등급별 나이는 차이가 없다.
- 대립가설: 객실 등급별 나이는 차이가 있다.
범주형 -> 범주형
x 범주형과 y범주형 간의 관계를 분석할 때, 수치형에서는 범주형의 자유도를 떠올리면서 (x범주형의 자유도) (y범주형의 자유도) 를 통해 판단하는 카이제곱통계량을 떠올린다.
카이제곱통계량 > {(x범주형의 자유도) (y범주형의 자유도)} * 2~3 이면, 차이가 있다.
- 귀무가설: 객실 등급과 생존여부(혹은 생존율)가 아무런 관련(차이)이 없다.
- 대립가설: 객실 등급과 생존여부가 관련이 있다.
수치형 -> 범주형
x 수치형과 y 범주형 간의 관계를 분석할 때, 시각화에서는 큰 의미를 두지 않는다는 것을 떠올리며 hue 매개변수를 떠올린다. 특별한 가설 검증 도구가 없어서 수치화에서는 로지스틱회귀로 p-value를 구한다.
- 귀무가설: 해당 변수의 회귀 계수가 0이다. (범주형 y와 아무런 관련이 없다)
- 대립가설: 해당 변수의 회귀 계수가 0이 아니다. (관련이 있다)
