이틀에 걸쳐 공부했지만 역시 난 통계에 너무 약한 거 같다 (분명히 고등학교 때 국어는 잘했는데 ..) 그래도 최대한 아는 내용 선에서 써보겠다!
📘 참고서적
- 딥러닝을 위한 수학 - 신경망 수학기초부터 역전파와 경사하강법까지
확률분포
-
확률분포란?
확률 변수가 특정한 값을 가질 확률을 나타내는 함수 (값들은 무작위로 생성된다. 흔한 예로 주사위의 눈이 나올 확률이다.)- 확룰분포의 근사로 취급 (히스토그램으로 표현)
- 이산확률분포 (정수 생성)
- 연속확률분포 (부동소수점 생성)
히스토그램
해당 표는 명확한 '대칭성'을 보여준다. 히스토그램은 이산적인 분류함(bin)들 각각에 몇 개의 항목이 들어갔는지를 보여주는 그래프이다. 이미지의 픽셀 값 분포를 살펴볼 때 자주 쓰인다.
이산확률분포
이산확률분포는 '개별 정수값에 특정 확률을 배정'하는 것과 같다. 이는 연속분포와 다른 점이기도 하다. 이산확률분포는 다음 세 가지로 나뉜다.
- 이항분포 (binomial distribution)
- 베르누이 분포 (Bernoulli distribution)
- 푸아송 분포 (Poisson distribution)
🏷️ 이항분포 (binomial distribution)
이항분포를 수식으로 표현하면 위와 같다.
각 사건에 구체적인 확률(p)이 배정된 상황에서 주어진 횟수(n)만큼 시행(x)을 거듭할 때 각 사건의 기대 빈도를 나타낸다.
즉, 발생확률 p인 사건이 n번의 시행 중에 x번 발생할 확률을 의미!
🏷️ 베르누이 분포 (Bernoulli distribution)
베르누이 분포는 이항분포의 특수 사례이다.
위의 식에서 n을 1로 고정하면 된다. 해당 분포는 이분법적인 결과(0 or 1 / 사건이 발생하지 않는가 or 발생하는가)를 낼 때 매우 유용하게 쓰인다.
🏷️ 푸아송 분포 (Poisson distribution)
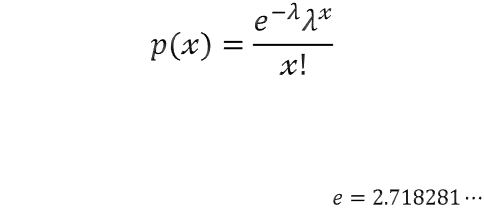
푸아송 분포를 수식으로 표현하면 위와 같다.
푸아송 분포는 임의의 특정 시행에서 사건이 발생할 확률은 구체적으로 알지 못하고, 일정 구간에서 사건의 평균 발생 횟수만 알고 있을 때 사용된다. 주로 방사선 붕괴 실험에 자주 쓰인다.
일정한 시간 구간에서 사건이 발생한 횟수를 평균적으로 λ라고 하면, 그 시간 구간에서 사건이 x번 발생할 확률을 의미!
연속확률분포
연속확률분포는 특정한 하나의 값이 선택되는 것이 아닌, 선택된 값이 '특정한 범위에 속하는' 것과 같다.
위의 그림은 연속확률분포의 가장 대표적인 예시인 🔵감마🔵(파랑), 🔴베타🔴(빨강), 🟡정규🟡(노랑)분포를 나타낸 그래프이다. (그래프에 표시되지는 않았지만, 일자형에 가까운 고른 분포도 존재한다.)
연속확률분포는 하나의 값이 특정 구간에 속할 확률이 구간에서 곡선 아래의 면적에 해당한다. 이를 구하기 위해서는 '적분'이 필요하다.
(책에서는 정규분포에 대한 내용만 자세하게 다루어서, 개인적으로 감마분포, 베타분포에 대한 내용을 짤막하게나마 첨부한다.)
🏷️ 감마분포 (Gamma distribution)
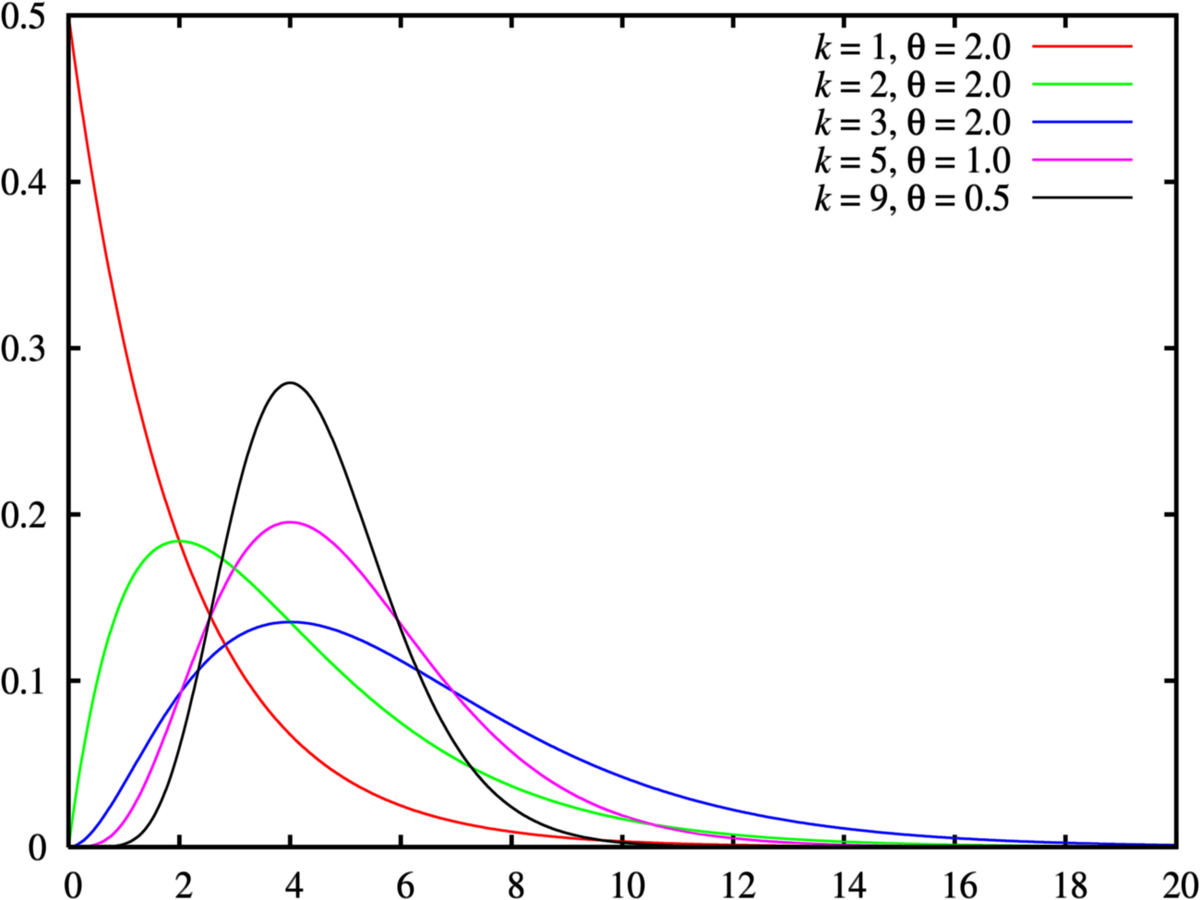
위의 사진과 같이 왼쪽으로 분포가 치우쳐 있는 것을 우리는 '감마분포'라고 부른다. 일반화하면 안 되지만 여튼 말이다
감마분포를 알기 전에 알아야 할 것은 바로 '감마함수'이다.
감마함수는 팩토리얼 함수를 복소수까지 확장 시켜 만든 새로운 함수이다. 아래 식과 같이 표현할 수 있다.
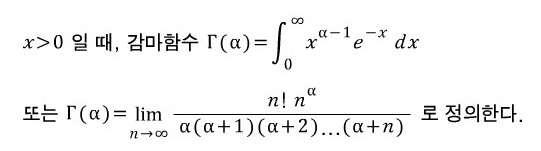
감마분포는 2개의 매개변수로 이루어져 있다. 하나는 곡선의 형태(k), 또 다른 하나는 축척 또는 규모(s)라고 결정한다.
k가 클수록 감마곡선의 융기부가 중앙으로 이동해 정규분포의 곡선과 모양이 비슷해진다. 또, s는 융기부의 너비에 관여한다.
그렇다면 대체 감마분포는 무엇일까?
α번째 사건이 일어날 때까지 걸리는 시간에 대한 연속확률분포를 의미!
감마함수, 감마분포의 정의와 특징에 관련하여 설명을 잘 해둔 블로그가 있어 링크를 첨부한다.
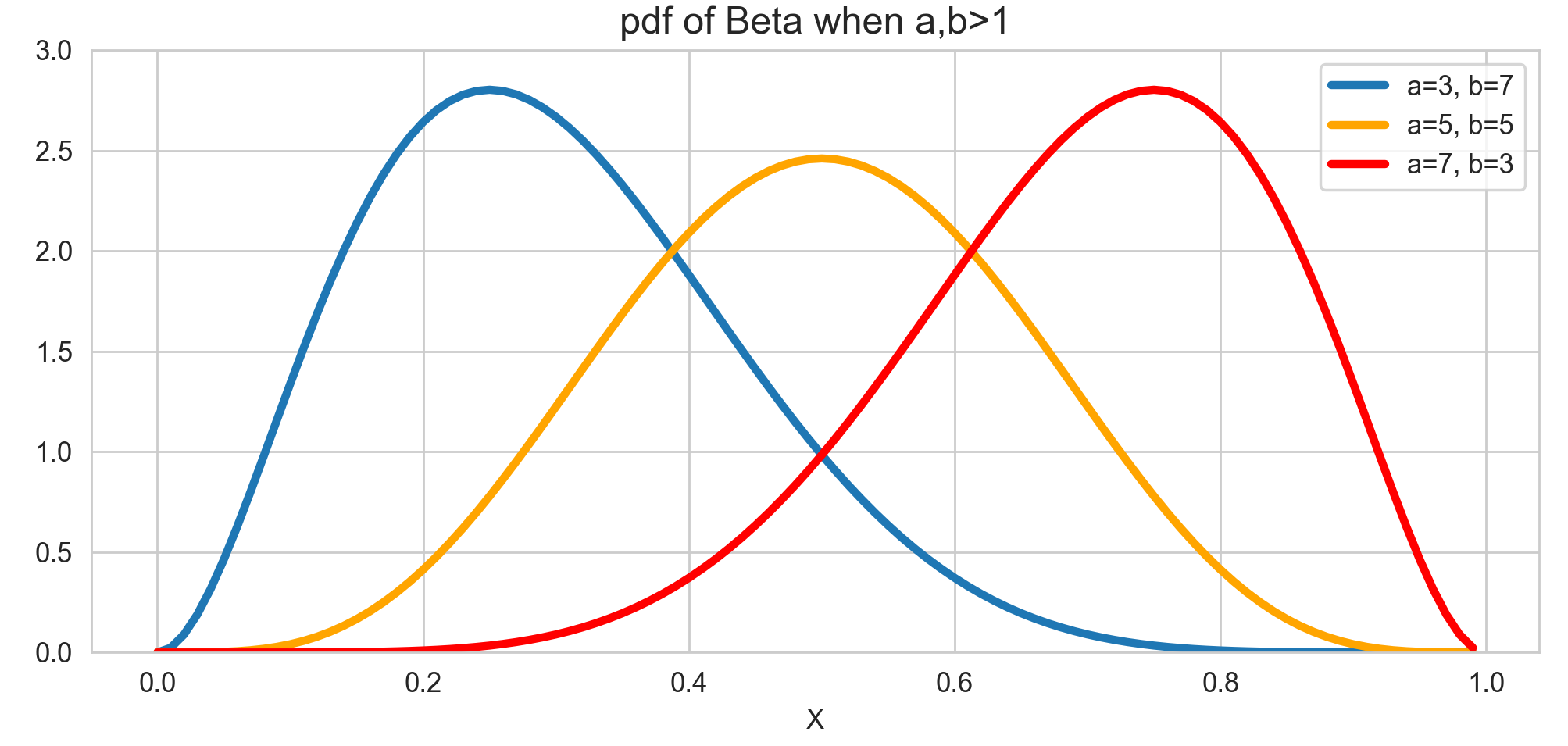
🏷️ 베타분포 (Beta distribution)
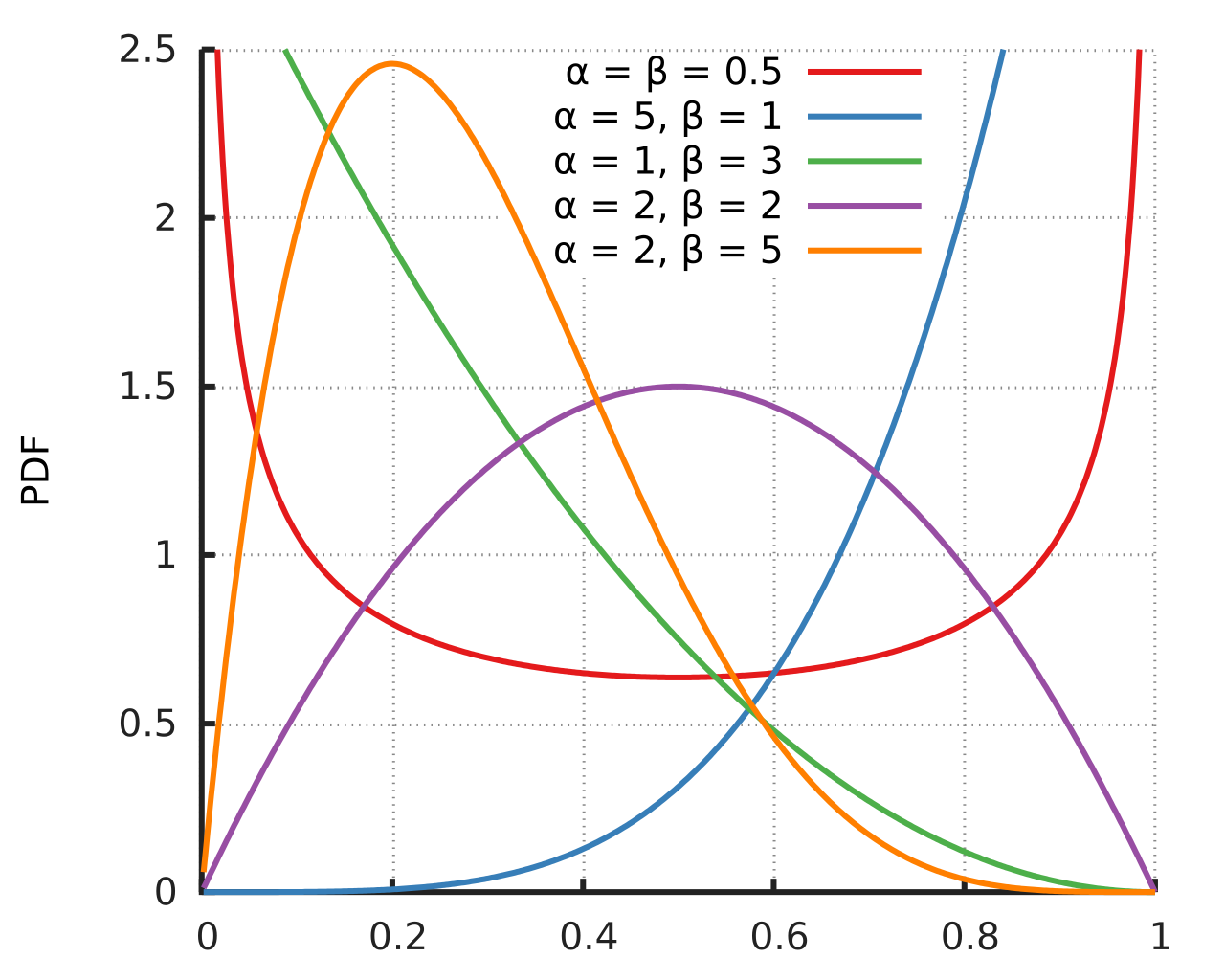
베타분포는 사실 정확히 뭔지를 잘 모르겠다. 모양이 중구난방 내 정신머리 같음
베타분포를 알기 위해서는 역시 베타함수를 알아야 한다. 베타함수는 내가 고등학교 때 배웠던 이항계수를 실수 범위까지 확장한 함수이다. 아래 식과 같이 표현할 수 있다.
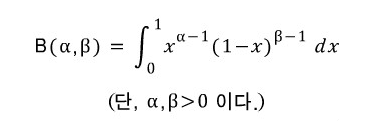
베타분포 역시 두 개의 매개변수를 사용한다. 이를 각각 a, b라고 결정한다.
- a > b일 때
베타곡선의 융기부가 오른쪽으로 치우침 - a < b일 때
베타곡선의 융기부가 왼쪽으로 치우침 - a==b일 때
정규분포가 됨
베타함수에 대해서는 잘 모르겠어서, 참고한 블로그 링크를 올린다.
- https://blog.naver.com/PostView.nhn?isHttpsRedirect=true&blogId=mykepzzang&logNo=220843077734
- https://soohee410.github.io/beta_dist
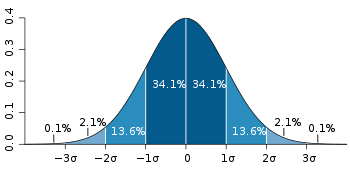
🏷️ 정규분포 (Normal distribution)
정규분포는 가우스 곡선 혹은 종 곡선으로 불리는데, 곡선의 모양이 똑 닮았기 때문이다. 그림은 아래와 같다.
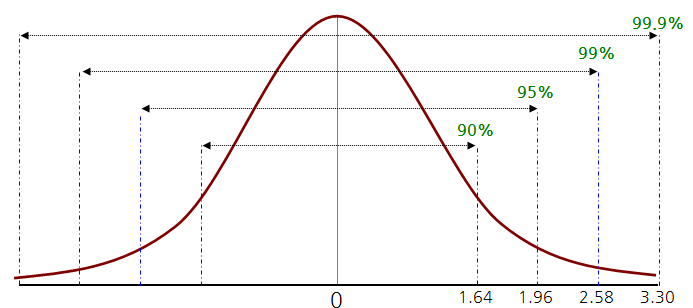
정규분포는 평균, 표준편차가 주어졌을 때 엔트로피를 최대화하는 분포이다.
정규분포는 다섯 가지 특징을 갖고 있다.
- 평균을 중심으로 좌우 대칭 (Symmetric)
- 종 모양 (Bell Shaped)
- 봉우리가 하나 (Single Peaked)
- 모든 곡선의 넓이는 1
- 그래프가 0에 닿을 거 같아 보이지만 실제로는 아님 (0.0001에 속함)
그 외 알아두면 좋을 내용들
중심극한정리 (Central Limit Theorem)
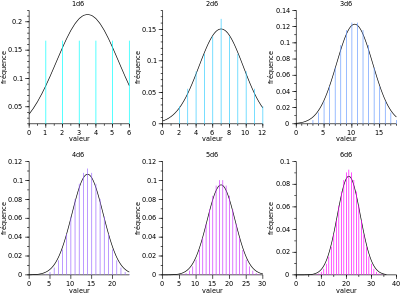
중심극한정리는 간단하게 말해서, 표본의 크기 N이 커질수록 곡선의 모양이 정규분포에 가까워지는 것이다.
이는, 표본평균집합에서 생성한 확률 분포는 표본을 추출한 실제 바탕 표본의 형태와는 무관하게 점점 정규분포에 가까워진다는 의미와도 같다.
이를 통해 알 수 있는 점은 표본크기 N이 커지면 커질수록 표준오차가 점점 더 줄어들어서 모수 예측이 정확해진다는 것이다.
큰 수의 법칙 (Law Of Large Number)
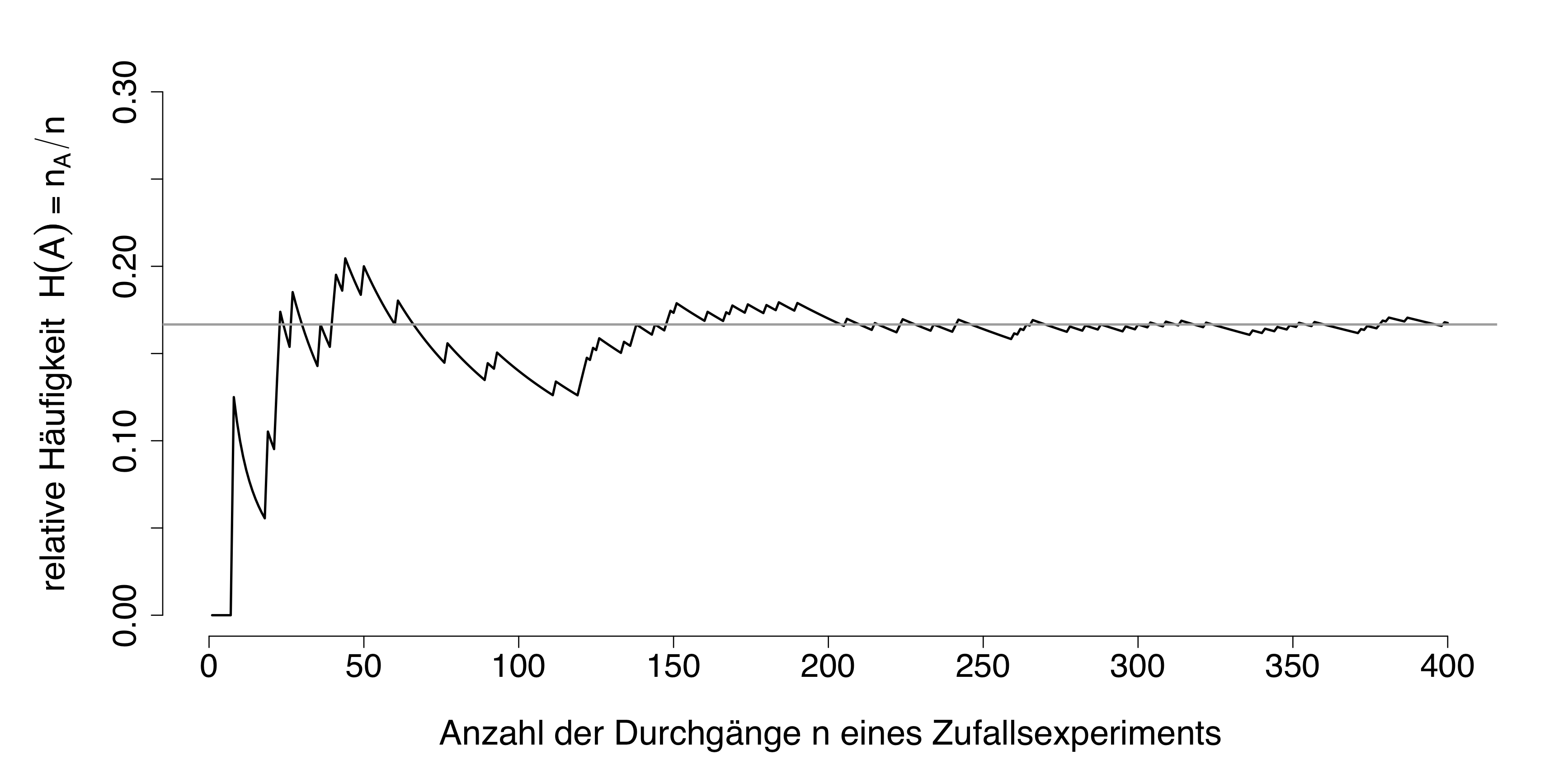
분포에서 추출한 표본의 크기가 클수록 표본평균이 점점 평균에 가까워지는 것이다.
중심극한정리 VS 큰 수의 법칙
- 중심극한정리
분포에서 다수의 표본을 추출했을 때, 그 표본평균들의 분포가 어떠한가? - 큰 수의 법칙
분포에서 추출한 표본 하나의 평균과 모평균의 관계가 어떠한가?
🗂️ 중심극한정리 VS 큰 수의 법칙 정리
- 중심극한정리
크기가 큰 표본 N을 추출했을 때, 그 표본평균의 분포가 정규분포에 가까운가?- 큰 수의 법칙
자신이 추출한 표본 N의 크기가 크면 클수록 모평균이 표본평균에 점점 가까운가?
다음은 전에 한 번 다루었던 베이즈 정리와 이를 기계학습에 적용시킨 베이즈 분류기에 대한 내용을 소개하겠다!
