매출하락 최소화 - kakao blind recruitment 2021 - python

intro

이 글을 읽었으면 하는 사람은 최소한 이 문제를 풀려고 시도해보다가 도저히 안되겠을때 포인트를 얻어가려는 사람이 읽으면 좋겠다고 생각한다. 그러므로 문제 설명은 하지 않을 것 이고 바로 문제풀이로 들어간다. 마지막 문제라 굉장히 막막할 수 있는데 카카오의 마지막 문제 치고는 극악의 난이도는 아니다. DP와 트리구조에 대한 기본적인 이해가 있으면 누구든 이 문제를 풀 수 있다.

문제 링크

https://programmers.co.kr/learn/courses/30/lessons/72416

풀이

포커스되는 n번 노드는 팀장이라고 치자.
팀장이 포함되는 경우

• 팀원들이 포함이 될수도 있고 안될수도 있다. (팀원들이 또 그 팀의 팀장인 경우 다른팀에서 포함될 수 있기 때문)
• 결국 자식들의 모든 combination을 조합해 최소값을 구한다

팀장이 포함되지 않는 경우

• 팀원들중 한명은 꼭 참여해야 한다.
• 그러므로 자식노드들이 모두 참여 안함을 제외한 나머지 모든 combination을 조합해 최소값을 구해야 한다.

팀장이 될 수 없는 경우 (리프노드인 경우)

• 포함이 되는 경우 자신의 판매량이 곧 최솟값이고 포함이 안되는 경우는 0이다.
• 별도로 처리해준다.

case1 : DP[n][0] => n번 노드가 포함이 되는 최소값
case2 : DP[n][1] => n번 노드가 포함이 되지 않는 최소값

그림으로 보면 노드별로 다음과 같은 숫자가 나와야한다.
노드 위의 빨간 번호는 (dp_include_self, dp_exclude_self)
(직접 손으로 해보길 바란다..)

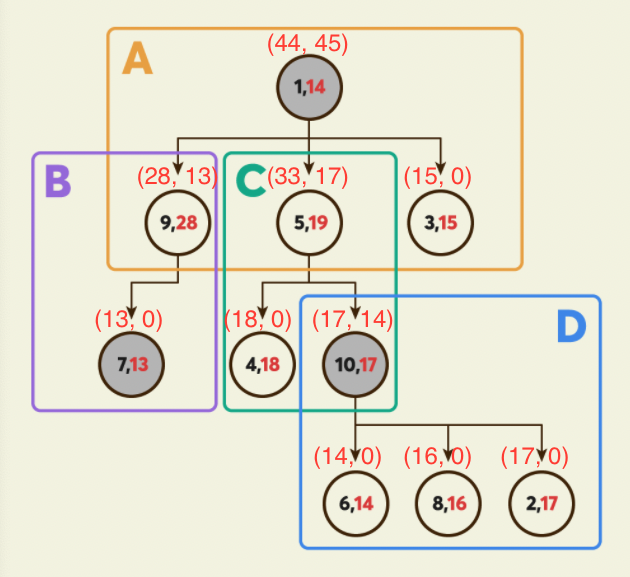
point

• 후위순회로 탐색해야 리프노드일때와 아닐때로 계산을 할 수 있다.

위의 방식을 그대로 구현해보면

위와 같이 case 18~20에서 시간초과가 난다.
괜찮다. 나머지 90%는 맞았기 때문에 접근방식(logic)은 맞았다는 것 이다.
당황하지 않고 이제 어디부분에서 조금 더 효율적이게 돌릴 수 있을까를 찾으면 된다.

최적화

현재 팀장이 포함인경우 모든 children의 combination을 구한다.
생각해보면 팀장이 이미 포함되었기 때문에 바로 아래 자식들도 포함되는 경우는 그 자식들이 다른 팀의 팀장으로 포함되는 경우일 것 이다. 그렇다는건 리프노드는 combination에 포함 할 필요가 없다는 말이다.

그렇다면 현재 팀장을 포함하지 않는 경우에도 성립할까?
성립하지만 예외가 있다.
최소한 팀내에서 한명이상은 워크숍에 포함되어야 하기 때문에 combination에서 제외는 하지만 leaf node들중 하나가 대표로 나가고 나머지 internal node들은 포함하지 않는 경우 하나만 생각해주면 된다.

정리해보자

1. n번째 노드는 항상 팀장노드이고 자신이 포함될때, 안될때 두가지로 DP를 한다.
2. 리프노드인경우 dp[n][0] = nodes[n].sales, dp[n][1] = 0 이다.
3. 후위순외로 돌아야 internal node의 계산을 정상적으로 할 수 있다.
4. combination을 internal children의 조합으로 구한다.
5. 자신을 포함하지 않는경우 leaf 노드중 최소값 하나가 포함되는 경우를 예외처리 해준다.

Before

After

Code

import sys
from dataclasses import dataclass, field
from itertools import combinations
from typing import List


@dataclass
class Node:
    sales: int
    dp_include_self: int = field(default=sys.maxsize)
    dp_exclude_self: int = field(default=sys.maxsize)
    children: list = field(default_factory=list)
    parent: int = field(default=-1)


def calculation_sales(idx: int, sales: int, include_set: set, nodes: List[Node]) -> int:
    exclude_set = set(nodes[idx].children) - include_set
    for child in include_set:
        sales += nodes[child].dp_include_self
    for child in exclude_set:
        sales += nodes[child].dp_exclude_self

    return sales


def dfs(idx: int, nodes: List[Node]) -> None:
    # 리프노드인 경우
    if not nodes[idx].children:
        nodes[idx].dp_include_self = nodes[idx].sales
        nodes[idx].dp_exclude_self = 0
        return

    # 자식들 먼저 순회
    for child in nodes[idx].children:
        dfs(child, nodes)

    # leaf node인 child와 internal node인 child를 구별
    children = set(nodes[idx].children)
    leaf_children = set((child for child in children if not nodes[child].children))
    internal_children = children - leaf_children
    internal_child_count = len(internal_children)

    combs = []  # combination
    for i in range(internal_child_count + 1):
        combs += list(combinations(internal_children, i))

    # 자신을 포함하는 경우 (사실 이것도 한줄로 가능..)
    for comb in combs:
        _sales = calculation_sales(idx=idx, sales=nodes[idx].sales, include_set=set(comb), nodes=nodes)
        nodes[idx].dp_include_self = min(nodes[idx].dp_include_self, _sales)

    # 자신을 포함하지 않는 경우
    for comb in combs:
        if not comb:  # 최소 한개 자식은 포함되어 있어야 함
            continue
        _sales = calculation_sales(idx=idx, sales=0, include_set=set(comb), nodes=nodes)
        nodes[idx].dp_exclude_self = min(nodes[idx].dp_exclude_self, _sales)

    # 자신을 포함하지 않는 경우에서의 예외처리 (리프노드 하나만 포함하고 나머지는 포함하지 않는 경우)
    if leaf_children:
        leaf_children_min_sales = min((nodes[child].sales for child in leaf_children))
        _sales = sum(map(lambda child: nodes[child].dp_exclude_self, internal_children)) + leaf_children_min_sales
        nodes[idx].dp_exclude_self = min(nodes[idx].dp_exclude_self, _sales)


def solution(sales, links):
    nodes = [None] + [Node(sales=sale) for sale in sales]  # 구현 편의상 인덱스가 1부터 시작
    for parent, child in links:
        nodes[parent].children.append(child)
        nodes[child].parent = parent

    dfs(1, nodes)

    return min(nodes[1].dp_include_self, nodes[1].dp_exclude_self)