
Intro
이번 포스트에서는 지난편의 목적함수가 어떻게 Global Optimal을 갖는지 알아보겠다. 목적함수를 뜯어봐야하기 때문에 이전 포스트의 목적함수를 그대로 가져오겠다.
Object Function
Object function discription 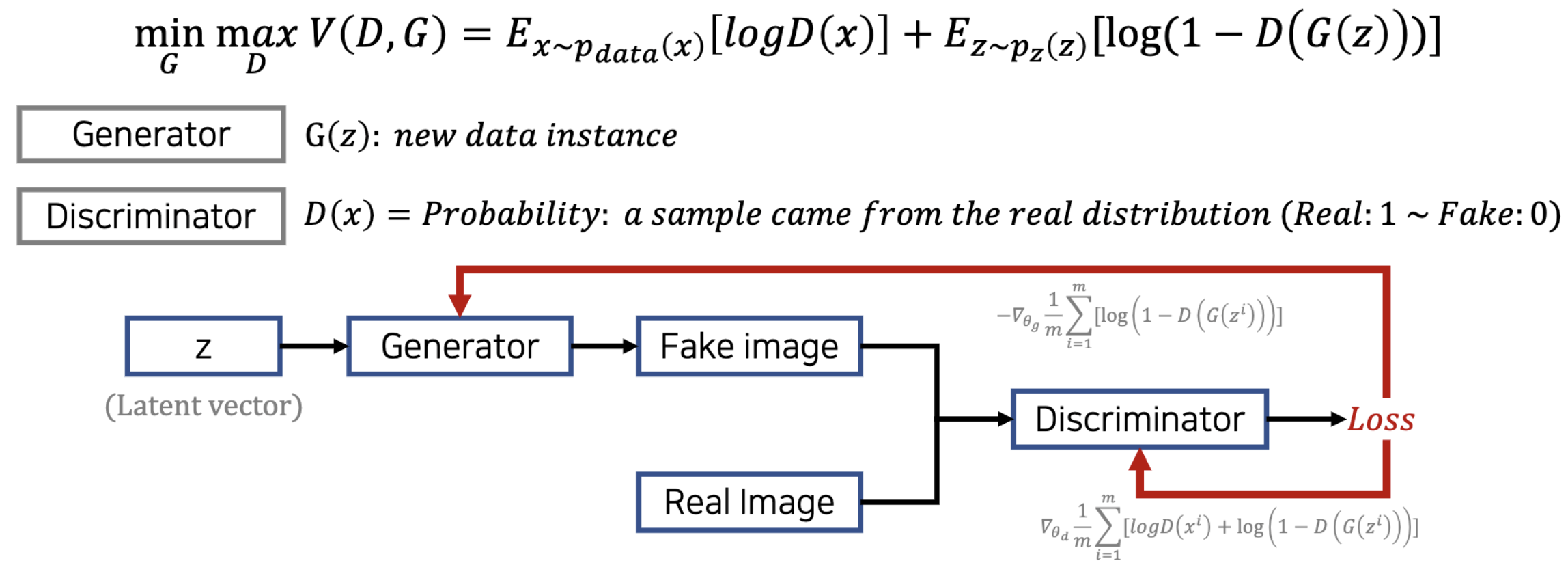
-
Discriminator는 Real Image는 1 Fake Image는 0으로 분류하도록 학습해야하기 때문에 위의 두 기댓값중 앞의 기댓값(원본 이미지)은 1이 되도록, 뒤의 기댓값(Generator가 만든 가짜 이미지)은 0이 되도록 목적함수가 설계되어있다. [Maximizing]
-
Generator는 뒤의 기댓값만 보면 된다. 최대한 Discriminator가 1으로 내뱉을 수 있도록 Discriminator의 학습을 교란시킨다. (이러한 컨셉에서도 서로 Adversarial의 컨셉이 들어가 있다) [Minimizing]
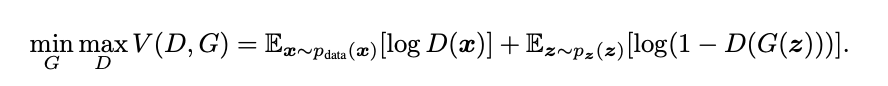
수식이라는게 직접 써야 이해가 되는 부분이 있어서 나의 아름다운 필채와 함께 설명을 해보겠다.
Decompose Object Function

설명이 모호한부분은 첫줄의 변환은 이산확률분포에서 연속확률분포식으로의 변환이다.
Discriminator는 목적함수를 최대화 시켜야한다. 위의 식은 목적함수를 미분해 극댓값을 구하는 과정이고 그 결과 일때 최적이라는 식이 나온다.
는 원본 이미지고 는 가짜 이미지인데 약간 precision, recall과 비슷하다는 느낌도 든다. 만약 나중에 가짜 이미지의 분포가 원본 이미지의 분포와 비슷하게 된다면 == 가 되어 에 수렴이 될것이다.

그렇다면 이제 == 로 학습한다는걸 증명해야한다.
이번 증명에서는 KL Divergence와 Jensen Shannon Divergence라는걸 활용한다.
이번 주제가 Divergence를 설명하는건 아니기 때문에 자세한 설명은 생략하고 왜 사용하는지부터 알아보자.
KL Divergence는 Distance metric이 아니다. 단지 정보량의 차이를 계산하는 함수이다. 우리가 실제로 사용할 metric은 JSD(Jensen Shannon Divergence)이고 JSD자체가 KL Divergence를 사용하기 때문에 먼저 KL Divergence로 표현하는 식으로 바꾸고 그다음 JSD식으로 변환한다.
최종적으로 라는 식이 나오는데 거리가 최소값이 나오려면 일때 최소값인 를 갖는 것 이다.
Code
code
Todo : code 설명
Outro
GAN은 Vision분야에서 빼놓을 수 없는 혁신적인 논문이다. 실제 논문에서는 GAN에서 사용한 방법들이 되는 이유가 대강 설명되어 있는 느낌인데 후속으로 나오는 다양한 논문들에서 이 내용들을 보충하기 때문에 더 찾아봐야 할 것 같다.
DCGAN, LSGAN, SGAN, ACGAN, CycleGAN 등등 다양한 GAN방법들이 나오고 더더욱 똑똑한 Generation 방법들을 제안한다. Vision분야를 꿈꾸는 학생이라면 GAN 논문을 완벽하게 이해하고 후속으로 나오는 방법론들을 꼭 읽어보길 추천한다.
