문제

문제 링크

해설

• 굉장히 어려운 문제였습니다. 행과 열에 대해 각각 2²⁰가지 조합을 어떻게 시간초과 없이 해낼 것인지 도무지 감을 잡기 어렵기 때문입니다.

• 문제를 풀기 위해서는 세 가지 아이디어가 필요합니다.

  1. 앞면(H)/뒷면(T) 두 가지 상태가 있다는 점에서 이진법(bool)을 생각해야 하고,
  2. '뒤집는 연산'은 비트연산자 '~'(NOT)으로 가능하며,
  3. 행을 임의의 조합으로 뒤집으면, 열은 조합이 자동으로 결정된다는 점입니다.

• 위 3번이 특히 이 문제의 핵심입니다.
  

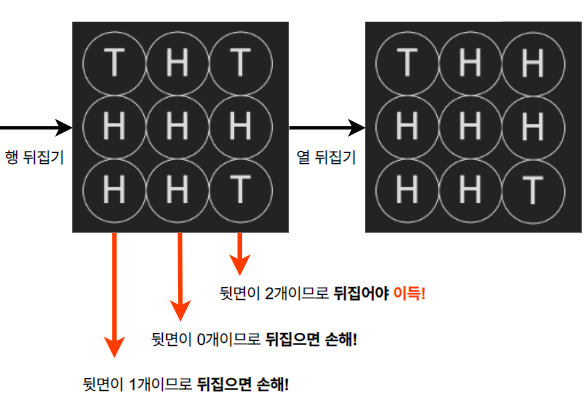
  • 행을 임의의 조합으로 뒤집었다고 가정합시다.
  • 0번 열은 뒷면이 1개이므로 뒤집으로 오히려 손해입니다. 1번 열도 마찬가지입니다.
  • 2번 열은 뒷면이 2개이므로 뒤집어야 뒷면이 1개로 줄어들어 이득입니다.
  • 이런 의미에서 행을 먼저 뒤집으면, 열은 조합이 자동으로 결정됩니다.
  • 즉, 우리가 예상했던 것과 달리 열에 대해 2²⁰가지 조합을 생각할 필요가 없습니다.

• 여기까지 아이디어를 떠올리고 이해했다면, 나머지는 정말 간단하게 재귀문으로 구현할 수 있습니다.

• 0번 행부터 (N - 1)번 행까지 (1 << N)가지 조합을 재귀함수를 이용해서 구합니다.

• 이때, k번째 행을 뒤집고 → 재귀함수 호출 → 다시 뒤집으면 복구됩니다.

• 행에 대한 뒤집는 조합을 구했다면, 이제 열 뒤집기를 시작합니다.

  • 열 뒤집기는 행 뒤집기와 다르게, 조합이 자동으로 결정된다고 말씀드렸습니다.
  • 즉, k번째 열의 '뒷면(T)' 개수에 따라 뒤집는 것이 이득이라면 뒤집고, 아니라면 뒤집지 않습니다.
  • 따라서 해당 행 조합에서 최소한의 뒷면 개수를 구할 수 있습니다.

코드

#include <iostream>
using namespace std;

int N, coin[20], answer = 1e9;

void flip(int row) {
	// N개의 행 뒤집기가 끝났으니 N개의 열 뒤집기 시작
	if (row == N) {
		int cnt = 0;
		for (int x = 0; x < N; ++x) {
			int cntTemp = 0;
			// 임의의 열에서 뒷면 동전 개수를 'cntTemp'에 저장한 뒤
			for (int y = 0; y < N; ++y)
				if (coin[y] & (1 << x)) cntTemp++;
			// 앞면 동전 개수 or 뒷면 동전 개수 중 적은 쪽을 cnt에 더합니다.
			cnt += min(cntTemp, N - cntTemp);
		}
		answer = min(answer, cnt);
		return;
	}
	flip(row + 1);
	coin[row] = ~coin[row];
	flip(row + 1); 
}
int main() {
	ios::sync_with_stdio(false); cin.tie(nullptr);
	cin >> N;
	for (int y = 0; y < N; ++y) {
		string line;
		cin >> line;
		for (int x = 0; x < N; ++x)
			if (line[x] == 'T') coin[y] |= (1 << x);
	}
	flip(0);
	cout << answer << '\n';
}

소스코드 링크

결과