문제

문제 링크

해설

• 어떤 노드(선거구) A와 B가 서로 연결돼있는지 확인하기 위해서는 DFS 또는 BFS를 사용해야 합니다.
• 노드는 총 10개고 두 그룹으로 나누는 경우의 수는 2^10가지로 충분히 시간내에 풀 수 있습니다.
• 우선, N개의 노드를 두 그룹으로 나눈 뒤
  1. 각 그룹이 적어도 하나의 노드를 포함하고 있는지?
  2. 각 그룹에 포함된 노드들이 서로 연결돼있는지?
  3. 인구 차이 최솟값 갱신
• 위 세 가지 순서로 로직을 진행하면 됩니다.
• 그룹을 나누는 경우의 수는 재귀를 사용하면 편하고, 역시 Set - Call - Reset 전략을 사용하면 됩니다.

코드

#include <iostream>
#include <cstring>
using namespace std;

int N, populations[11], answer = 1e9;
bool regions[11][11], group[11], visited[11];

// 출발지 s와 목적지 e가 서로 연결돼있는지 여부 반환.
bool is_they_connected(int s, int e)
{
	if (s == e) return true;
	bool ret = false;
	visited[s] = true;  // 무한루프 방지용 방문표시
	for (int i = 1; i <= N; i++) {
		// 두 지역이 연결돼있고, 같은 선거구일 때
		if (regions[s][i] && group[s] == group[i] && !visited[i]) {
			ret = is_they_connected(i, e);	// DFS 수행
			if (ret) break;
		}
	}
	return ret;
}

void solve(int region_num)
{
	if (region_num == N + 1) {
		// 선거구 A, B에 적어도 하나의 지역이 포함돼있는지 검사.
		int cnt_a = 0, cnt_b = 0;
		for (int i = 1; i <= N; i++) (group[i]) ? cnt_b++ : cnt_a++;
		if (cnt_a == 0 || cnt_b == 0) return;
		
		// 선거구 A, B에 포함된 모든 지역이 서로 연결돼있는지 검사.
		for (int i = 1; i <= N; i++) {
			for (int j = 1; j <= N; j++) {
				if (i == j) continue;
				// 같은 선거구인데, 서로 연결돼있지 않다면 불가능한 경우의 수다.
				memset(visited, false, sizeof(visited));
				if (group[i] == group[j] && !is_they_connected(i, j)) return;
			}
		}
		// 선거구 A, B의 인구수 차이를 구하고 최소값 갱신.
		int sum_a = 0, sum_b = 0;
		for (int i = 1; i <= N; i++)
			(group[i]) ? (sum_b += populations[i]) : (sum_a += populations[i]);
		answer = min(answer, abs(sum_a - sum_b));
		return;
	}
	// region_num 지역을 선거구 B에 포함한 후 경우의 수 계산
	group[region_num] = true;
	solve(region_num + 1);
	// region_num 지역을 선거구 A에 포함한 후 경우의 수 계산
	group[region_num] = false;
	solve(region_num + 1);
}

int main()
{
	ios::sync_with_stdio(false), cin.tie(nullptr);
	cin >> N;
	for (int i = 1; i <= N; i++) cin >> populations[i];
	for (int i = 1; i <= N; i++) {  // 선거구를 인접행렬로 입력받는다.
		int edges;
		cin >> edges;
		while (edges--) {
			int region_num;
			cin >> region_num;
			regions[i][region_num] = true;
		}
	}
	solve(1);
	cout << ((answer == 1e9) ? -1 : answer) << '\n';
	return 0;
}

• 선거구 그룹은 bool타입 변수 group로 구분하는데, 0일 때 A그룹, 1일 때 B그룹으로 구분합니다.
• Set-Call-Reset 전략을 재귀함수에 사용했습니다. region_num 지역을 각 그룹에 set 시킨 뒤 다음 번 노드를 call한 뒤 reset 합니다.
• 그렇게 N개의 노드에 대한 조합을 만들면, 조건을 검사합니다.
• 두 노드 A, B에 대한 연결성 검사는 DFS로 검사합니다.

소스코드 링크

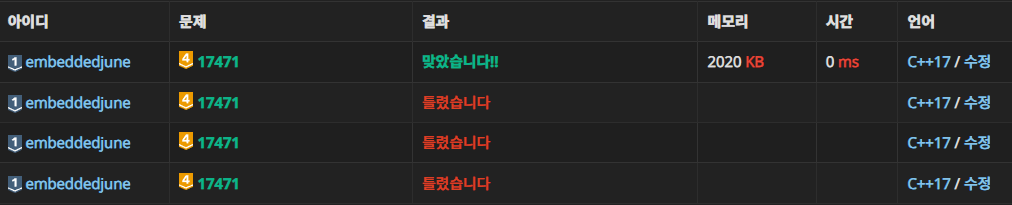
결과