문제

문제 링크

해설

• 까다로운 문제입니다.
  • (()(()과 (()()) 는 한 글자 차이인데 답은 2와 6으로 차이가 납니다.
  • 위 반례를 근거로 단순히 (, ) 문자로 스택에 push(), pop() 하는 방법으로는 어떤 (를 만났을 때 이후 ) 존재할 지 여부를 알 수 없다는 것을 알 수 있습니다.
  • 정리하자면, '올바른 괄호 문자열 길이'를 증가하는 판단기준을 명확히 정의하는 것이 이 문제의 핵심입니다.

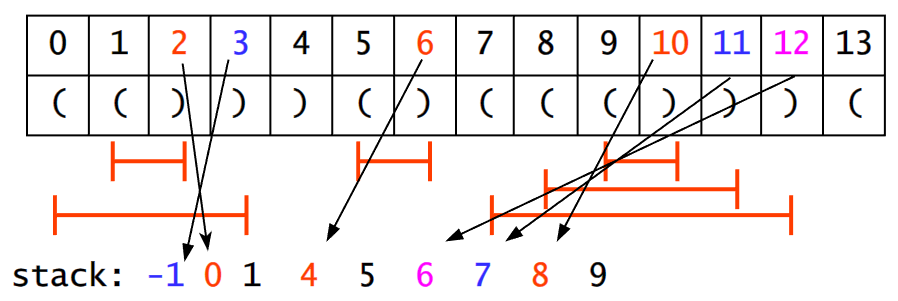
• 조금 난잡해서 이해하기 어려운 그림일 수 있지만, 핵심은 스택에 '인덱스 번호'를 넣는 것입니다. 그래야 길이를 구할 수 있으니까요.
• 가장 처음에 스택에 -1 를 넣어줍니다.
• 여는 괄호 (를 만났을 때는 무조건 스택에 인덱스 번호를 push() 합니다.
• 닫는 괄호 )를 만났을 때는 무조건 스택에서 요소 하나를 pop() 합니다.
  • 만일 스택이 비어있다면, 현재 인덱스 번호를 push() 합니다.
    • 왜냐하면, 방금 pop() 해서 스택이 비었다는 것은 부분적인 '올바른 괄호 문자열' 하나가 끝났음을 의미하기 때문입니다.
    • 연속해서 '올바른 괄호 문자열'이 올 수도 있고, 길이를 올바르게 계산하기 위해 현재 인덱스 번호를 넣어줘야 합니다.
    • 맨 처음에 -1을 넣어줬던 것과 같은 이치입니다.
  • 스택이 비어있지 않다면, 현재 인덱스 - 스택 top() 이 최댓값인지 갱신합니다.
  • 위 그림의 대응하는 화살표를 보면, 현재 인덱스 - 스택 top()은 올바른 부분 문자열의 길이를 의미합니다.
• 기존 방법과 비교해서 덜 직관적인 알고리즘이기 때문에 직접 손으로 그려보시면 조금 더 쉽게 이해하실 수 있을 것 같습니다.

코드

#include <iostream>
#include <stack>
using namespace std;

int main() {
    int N;
    cin >> N;
    
    string str;
    cin >> str;
    
    stack<int> stk;
    stk.push(-1);    // dummy
    
    int answer = 0;
    for (int i = 0; i < N; ++i) {
        if (str[i] == '(') stk.push(i);
        else {
            stk.pop();
            if (stk.empty()) stk.push(i);
            else answer = max(answer, i - stk.top());
        }
    }
    cout << answer << '\n';
}

소스코드 링크

결과