문제

문제 링크

해설

• N이 최대 50만이므로 O(N)~O(NlogN)에 풀어야 하는 어려운 문제였습니다.

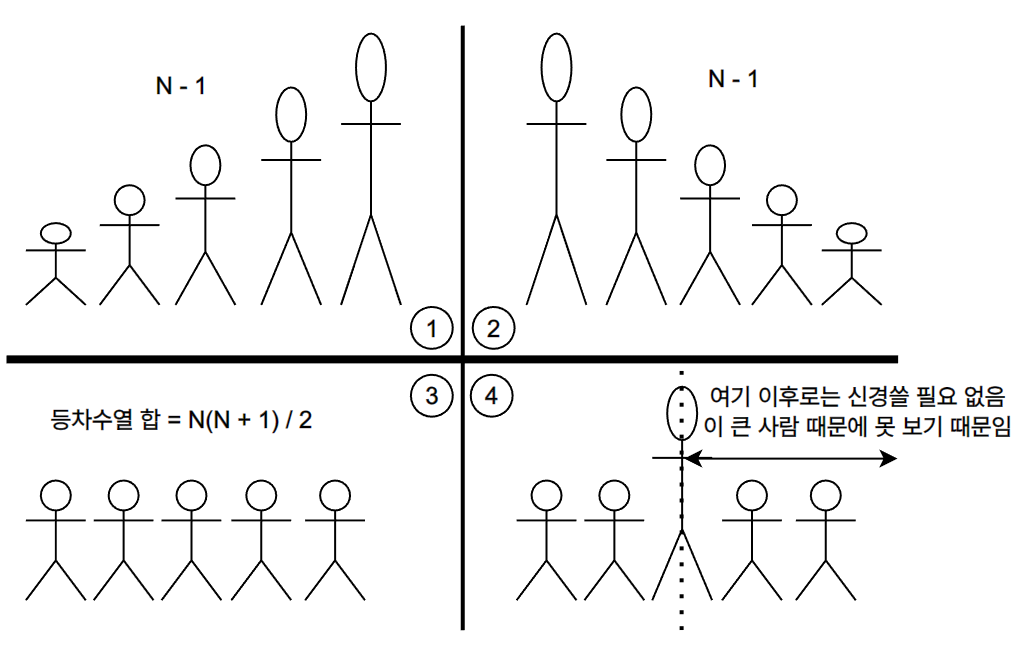
• 위와 같이 사람이 서 있을 수 있는 경우의 수는 4가지 입니다.
  • 1, 2번처럼 오름차순/ 내림차순으로 서있는 경우, 절대로 자기 옆사람 이외에는 다른 사람을 볼 수 없기 때문에 N명이 있을 때 N-1쌍이 만들어집니다.
  • 3번처럼 모든 사람의 키가 같을 경우, 모든 사람이 서로를 볼 수 있기 때문에 등차수열의 합 공식에 따라 N(N+1)/2쌍이 만들어집니다.
  • 4번이 가장 일반적인 형태, 중간에 키가 큰 사람이 있는 경우입니다.
    • 키가 큰 사람 오른쪽에 있는 사람은 신경쓰지 않아도 됩니다.
    • 왜냐하면, 어차피 그 사람 오른쪽에 있는 사람은 이 사람에게 가려서 안 보이기 때문입니다.
    • 따라서, 키가 큰 사람을 만났을 때, 어떠한 사건이 발생한다! 라는 점을 여기서 눈치채면 됩니다.
• 이 문제에 적절한 자료구조는 std::stack 스택입니다.
  • 스택에는 pair<int, unsigned long long> 형을 저장합니다.
  • 왜냐하면, 위 3번 등차수열 합 공식에 따라, 50만 명의 사람이 모두 같은 키일 경우 나올 수 있는 쌍의 개수가 int 범위를 초과하기 때문입니다.
  • 그리고, 데이터 두 개를 저장하는 이유는
    • 상호간에 키를 비교 하기 위해서는 '키' 정보가 필요하고,
    • 쌍의 개수를 구하기 위해서는 '쌍 개수' 정보가 필요하기 때문입니다.
• 스택이 비어있지 않거나, 입력된 키가 stack.top()보다 크거나 같다면, 작은 사람들을 pop() 하면서 카운팅을 해주면 됩니다.
• 이때, 입력받은 키와 같은 키는 특별하게 취급해야 합니다! 왜냐하면, 위 3번 그림과 같이, 키가 같을 때는 옆사람을 넘어서 더 많은 사람을 볼 수 있기 때문입니다. (아래 코드를 보면 조금 더 이해가 가실 겁니다.)

코드

#include <iostream>
#include <stack>
using namespace std;

int main() {
	ios::sync_with_stdio(false); cin.tie(nullptr);
	
	int N;
	cin >> N;
	
	// 50만 개 원소가 모두 동일할 때 등차수열 합만큼 답이 나오며 int 범위를 넘는다.
	stack<pair<int, unsigned long long>> stk;
	unsigned long long answer = 0;
	
	for (int i = 0; i < N; ++i) {
		int tall;
		cin >> tall;
		
		int cnt = 1;
		while (!stk.empty() && stk.top().first <= tall) {
			answer += stk.top().second;
			cnt = (stk.top().first == tall) ? stk.top().second + 1 : 1;
			stk.pop();
		}
		/* while() 문에서 스택은 빈 공간이 되게 되는데,
		  빈 공간이 아니라면, 요소들이 내림차순으로 배치돼있기 때문이다. */
		if (!stk.empty()) answer++;
		stk.push({tall, cnt});
	}
	cout << answer << '\n';
}

소스코드 링크

• 앞서 말씀드렸다시피 '쌍 갯수'는 int 범위를 초과할 수 있으므로 unsigned long long을 사용합니다.
• 입력받은 키가 현재 스택의 top()과 같다면, 3번 경우의 수에 해당하므로 top() 이 볼 수 있는 쌍의 개수에 1을 더해줍니다.
• 그 외에는 모두 자기 옆사람만 볼 수 있기 때문에 cnt = 1 입니다.
• 마지막 while()문 밖에 if() 문이 있습니다.
  • while()문은 1, 3, 4번 경우의 수는 대응할 수 있지만, 2번 경우의 수처럼 내림차순으로 사람들이 서있는 경우에는 진입할 수 없습니다.
  • 따라서, 일반적으로는 while()문을 지나면 스택이 빈 스택이 되는데, 빈 스택이 아니라면 answer를 1 증가시켜줘서 내림차순에 대한 예외처리를 해줍니다.

결과