문제

문제 링크

해설

• 우선 N, K의 범위가 30만이므로 적어도 O(N*logK) 알고리즘을 사용해야 하며, 최대 무게 Ci가 1억이고, 이게 K개 있을 수 있기 때문에 답은 int 범위를 넘을 수 있다는 점을 먼저 확인합니다.
  
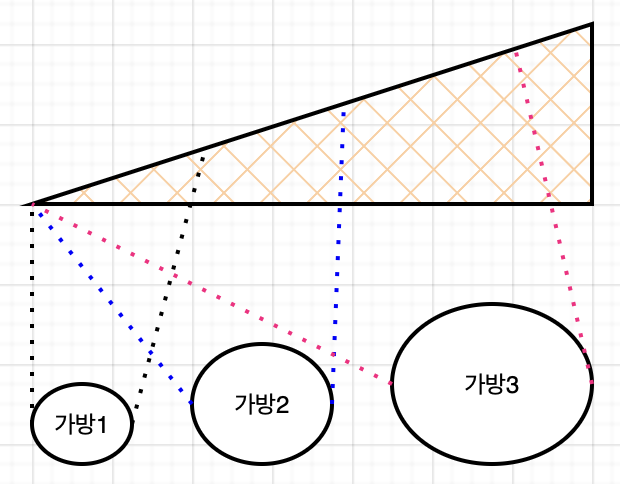
• 우선, 보석의 무게와 가방의 용량을 오름차순으로 정렬합니다.
• 위 그림처럼, n번째 가방에 담을 수 있는 보석들을 우선순위 큐에 넣습니다. 이때 우선순위 큐는 max heap(기본값)입니다.
• pop()을 하면, n번째 가방에 담을 수 있는 보석들 중 가장 가치가 높은 보석을 알 수 있습니다.
• 이를 K번 반복하면, 그리디하게 최적해를 구할 수 있습니다.
• 즉, 정렬에 O(NlogN), O(KlogK) 시간복잡도가 소요되고 오히려 정답은 O(K)에 찾을 수 있게 됩니다.

코드

#include <bits/stdc++.h>
using namespace std;
using ull = unsigned long long;

int main() {
	cin.tie(0)->sync_with_stdio(0);
	int N, K;
	cin >> N >> K;
	
	vector<pair<int, int>> jewel(N);
	for (int i = 0; i < N; ++i) cin >>jewel[i].first >> jewel[i].second;
	
	vector<int> bag(K);
	for (int i = 0; i < K; ++i) cin >> bag[i];
	
	sort(begin(jewel), end(jewel));
	sort(begin(bag), end(bag));
	
	ull ans = 0;
	priority_queue<ull> pq;
	for (int idx_jewel = 0, idx_bag = 0; idx_bag < K; ++idx_bag) {
		while (idx_jewel < N && jewel[idx_jewel].first <= bag[idx_bag])
			pq.emplace(jewel[idx_jewel++].second);
		if (!pq.empty()) ans += pq.top(), pq.pop();
	}
	cout << ans;
}

소스코드 링크

결과