문제

문제 링크
해설
- 문제를 풀기 전에 먼저 점의 위치가 음수 -10억부터 양수 10억까지 int 범위가 가능하기 때문에, 점의 위치를 나타내는 변수의 초깃값을
0으로 하는 실수에 유의합시다.
- 당연히 20억 + 1개의 점이 존재할 수 있기 때문에 수직선을 의미하는 배열은 만들 수 없습니다.
- 따라서 점들을 입력받은 뒤, 오름차순으로 정렬한 뒤 시작점부터 끝점까지 훑으면서 선을 합쳐나가며 총 길이를 구하면 O(N)에 문제를 해결할 수 있습니다.
- 대표적인 라인스위핑 알고리즘 문제인데, '훑는다'라는 추상적인 개념 덕분에 대부분의 라인스위핑 문제는 이렇게 어렵습니다.
- '정렬된 요소들을 시작지점부터 끝지점까지 일정한 방향으로 훑으면서 특정 조건을 만족하는지 판단해 기존 방법보다 빠르게 최적해를 구하는 알고리즘'으로 이해하면 되겠습니다.
- 어쨌든 우리는 모든 선을 오름차순으로 정렬한 뒤 겹치는 선들을 최대한 긴 직선으로 합칠 것입니다.
- 그러기 위해서는 시작점과 끝점에 대한 정보가 필요하므로
- 시작점은
sIdx, 끝점은 eIdx라는 변수로 나타내겠습니다.
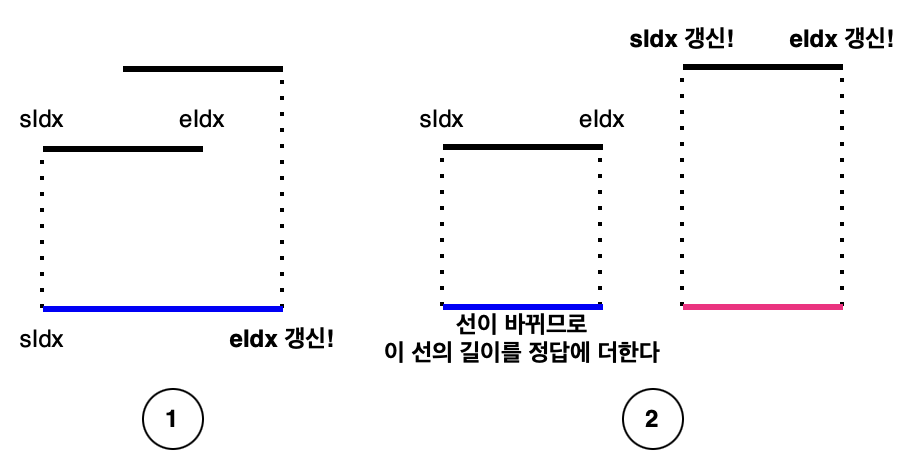
- 선이 겹칠 때는
eIdx만 갱신해주면 됩니다.
- 새로운 선으로 옮겨질 때는
sIdx, eIdx 모두 갱신해줘야 합니다. 또한, 지금까지 합쳐진 선의 길이를 정답에 더해줘야 합니다.
코드
#include <bits/stdc++.h>
using namespace std;
int main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int N;
cin >> N;
vector<pair<int, int>> vec(N);
for (int i = 0; i < N; ++i) cin >> vec[i].first >> vec[i].second;
sort(begin(vec), end(vec));
unsigned long long answer = 0;
int sIdx = -1'000'000'001, eIdx = -1'000'000'001;
for (const auto& line : vec) {
if (line.first > eIdx) {
answer += (eIdx - sIdx);
sIdx = line.first;
eIdx = line.second;
}
else if (line.first <= eIdx && eIdx <= line.second) {
eIdx = line.second;
}
}
answer += (eIdx - sIdx);
cout << answer << '\n';
}
소스코드 링크
결과