문제

문제 링크

해설

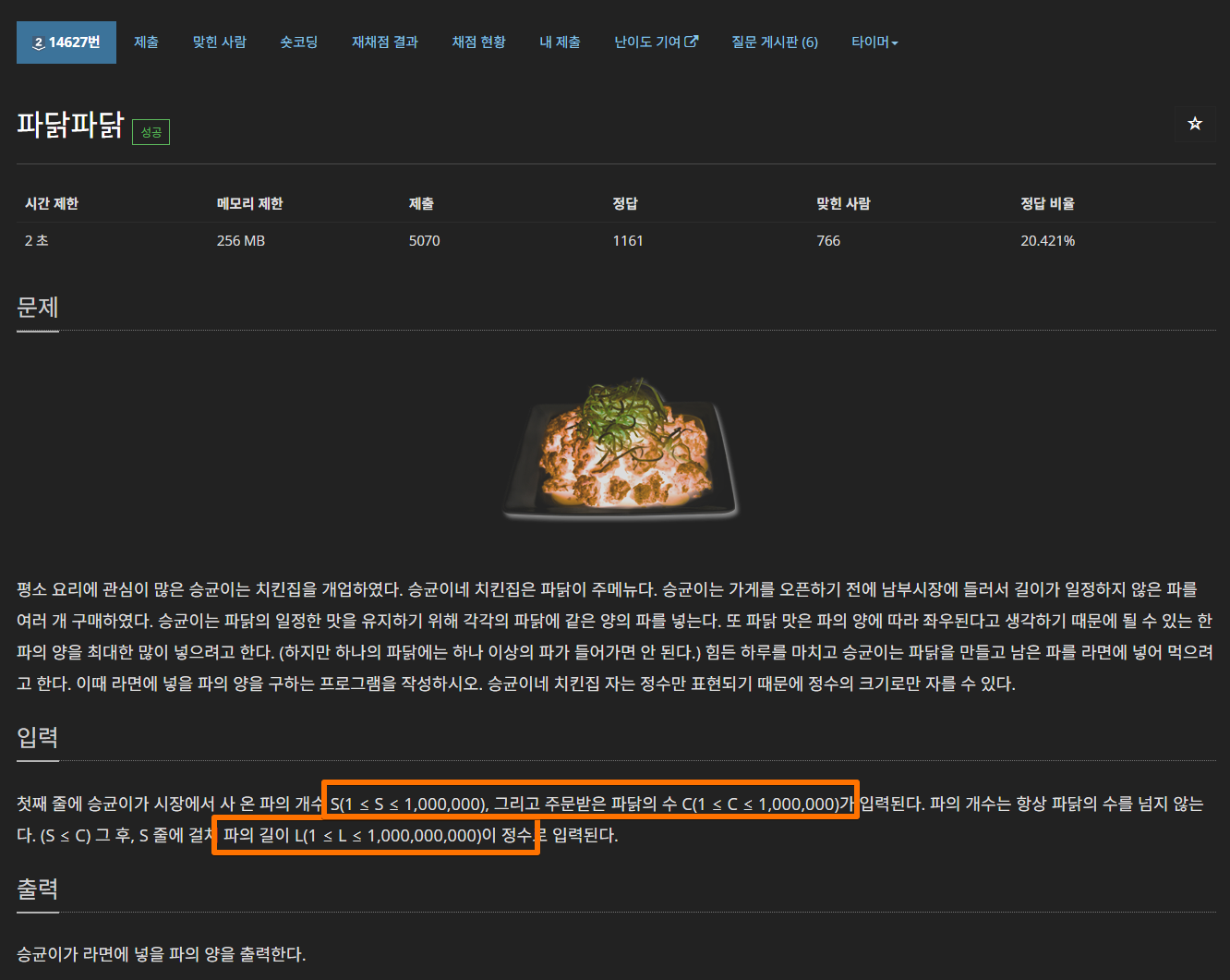
• 문제를 요약하면,
  • ' S개의 파를 길이 L의 파로 자를 때 C개의 덩어리를 만들 수 있는가? '
  • ' 이때 L의 최댓값을 구하고, 정답은 요소의 합 - L을 출력하시오. ' 입니다.
• L은 최대 10억, S는 최대 100만이기 때문에 일반적인 방법으로는 100% 시간초과가 날 것임을 알 수 있습니다. 그러므로 이분탐색을 이용해서 최적화문제를 결정문제로 변경합시다.
  • 즉, '파의 길이가 mid일 때, C개의 덩어리를 만들 수 있는가? Yes or No? '로 문제를 변경합니다.
• i번째 파를 길이 L인 파로 몇 개의 덩어리를 만들 수 있을까요? floor((double)파 / 파의 길이)로 계산할 수 있습니다. 왜냐하면, 소수점은 버려야 할 테니까요.
• 이렇게 최대 길이를 구했다면 전체 길이의 합에서 최대 길이 × C를 뺀 값을 출력하면 정답입니다.

주의할 점

• 이분탐색의 범위 중 오른쪽 범위의 포인터를 담당하는 high 변수의 초깃값에 대한 이야기를 하고 싶습니다.
• S와 C가 1부터 시작되는데, 둘 다 1인 경우에는 그냥 입력받은 파를 파닭에 넣으면 됩니다.
• 하지만, 저희의 이분탐색 알고리즘은 가장 처음에 mid 부터 시작되기 때문에, S와 C가 1인 경우를 처리할 수 없어서 실패가 뜰 것입니다.
• 따라서, high를 입력받은 S개의 파 중 최댓값의 2배로 설정해서 mid가 S개의 파 중 최댓값부터 시작할 수 있도록 처리합니다. 이렇게 하면 예외를 처리할 수 있습니다.

코드

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

int S, C, A[1'000'001]; 
ll low, high, mid, len, sum;

bool isAvailable() {
	ll cnt = 0;
	for (int i = 0; i < S; ++i) cnt += floor((double)A[i] / mid);
	return cnt < C;
}

int main() {
	cin.tie(0)->sync_with_stdio(0);
	
	cin >> S >> C;
	for (int i = 0; i < S; ++i) {
		cin >> A[i];
		sum += A[i];
		if (high < A[i]) high = A[i];
	}
	high <<= 1;
	while (low <= high) {
		mid = low + (high - low) / 2;
		if (isAvailable()) high = mid - 1;
		else low = mid + 1, len = mid;
	}
	cout << sum - len * C;
}

소스코드 링크

결과