문제

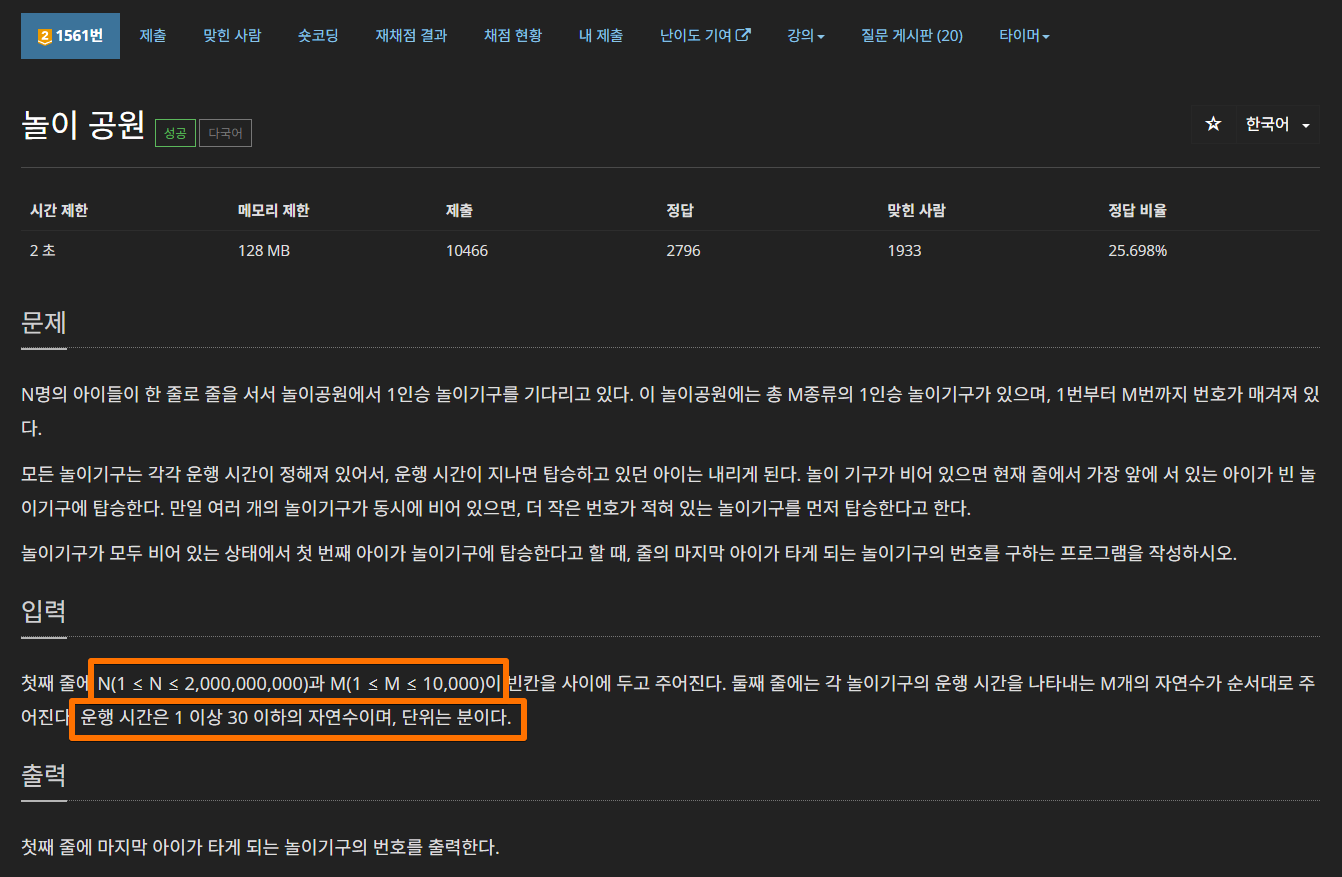
문제 링크

해설

• 어려운 문제입니다.
• 우선, 언듯 보기에는 차근차근 각 1분씩 진행하거나 또는 입력받은 M개의 놀이기구의 최소공배수씩 시간을 늘려가면서 N명의 아이들이 놀이기구에 탑승할 수 있도록 처리해야 할 것 같습니다.
• 하지만, N의 범위가 최대 20억까지이며, M도 1만까지므로 시간을 1분 또는 x분씩 늘려가면서 해결하는 문제는 아닌 것을 빠르게 알아차려야 합니다. 그리고 이분탐색을 이용한 결정문제 변환 전략을 떠올려야 합니다.
• ' 특정 시간 t분일 때 N명의 아이들이 모두 놀이기구에 탈 수 있는가? Yes or No? '를 판단합니다.
  • t분이 주어질 때, i번째 놀이기구에 탈 수 있는 아이들의 수는 t / 놀이기구[i] 입니다.
  • 하지만 주의해야합니다. t분이 끝나자마자 아이가 내리고 바로 연달아서 다른 아이가 이어서 타기 때문에 실제로는 (t / 놀이기구[i]) + 1 입니다. 한 명을 더 카운팅해야 한다는 뜻입니다.
  • 즉, t분에 탈 수 있는 모든 아이들의 수를 구하는 함수는 다음과 같습니다.

int count(int t) {
	int ret = M;     // 위에서 설명했듯, M개의 놀이기구가 마지막에 1명씩 더 타므로 초깃값 M
	for (int i = 0; i < M; ++i) ret += t / arr[i];
	return ret;
}

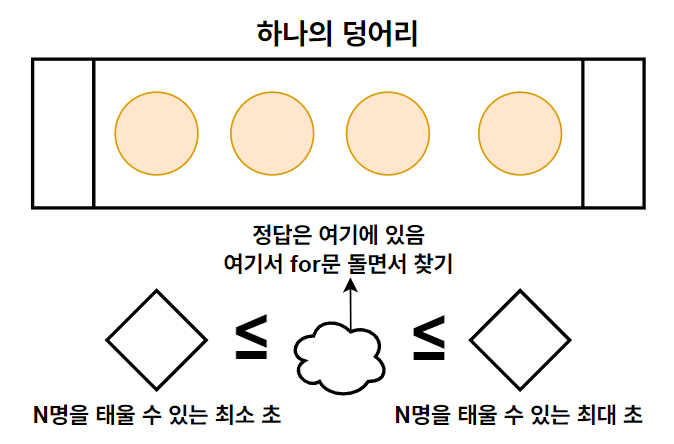
• 즉, 저희의 전략은 위와 같습니다.
  • N명을 태울 수 있는 최대 특정 시간 t분을 이분탐색을 이용해 구합니다.
  • 그리고, t - 1분일 때는 최대 몇 명을 태울 수 있는지를 구합니다.
  • 그 뒤부터는 for문을 돌면서 어떤 놀이기구가 N번째 학생이 타는 놀이기구인지 찾고 놀이기구 번호를 반환합니다.
  • (주석 꼭 참고해주세요)

코드

#include <bits/stdc++.h>
using namespace std;
using ull = unsigned long long;

constexpr ull MAX_TIME = 60'000'000'001;    // 20억 × 30분
constexpr int MAX_M = 10'001;

ull N, M, A[MAX_M];
ull low = 1, high = MAX_TIME, mid, ans;

ull countStudents(ull time) {
    ull ret = M;
    for (int i = 0; i < M; ++i) ret += time / A[i];
    return ret;
}

int main() {
    cin.tie(0)->sync_with_stdio(0);
    cin >> N >> M;
    for (int i = 0; i < M; ++i) cin >> A[i];

    if (N <= M) { cout << N; return 0; }

    while (low <= high) {
        mid = low + (high - low) / 2;
        if (countStudents(mid) < N) low = mid + 1;
        else high = mid - 1, ans = mid;
    }
    ull temp = countStudents(ans - 1);    // (ans-1)분일 때 최대 수용인원
    // temp + 1번째 학생부터는 ans분일 때의 덩어리에 포함됩니다. 
    for (int i = 0; i < M; ++i) {
        // 해당 놀이기구에 탈 수 있다면, 태우고 temp를 늘립니다.
        if (ans % A[i] == 0) temp++;
        // N번째 학생이라면 놀이기구 번호 출력하고 프로그램 종료합니다.
        if (temp == N) { cout << i + 1; break; }
    }
}

소스코드 링크

결과