Neural Network

Neural Network 영역은 원래 생물학적 신경계통을 모델링한다는 영감에서 시작되어 공학적으로 발전하여 기계학습 과제에서 좋은 성과를 얻고 있습니다.

뇌의 기본적인 계산 단위는 뉴런입니다.

각각의 뉴런은 10^14 - 10^15개의 시냅스와 연결되어 있으며 단일 생물학적 뉴런(위)과 이를 수학적으로 나타낸 이미지(아래)는 아래와 같습니다.

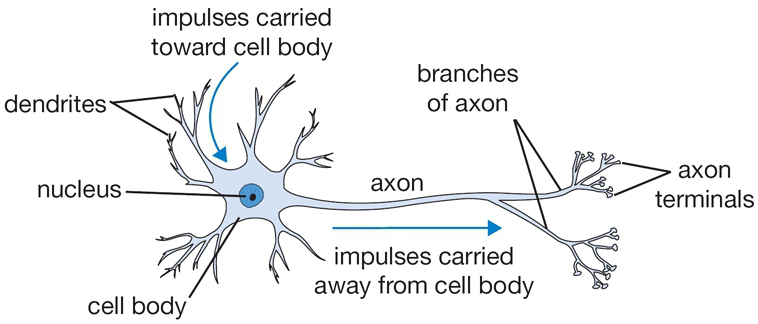
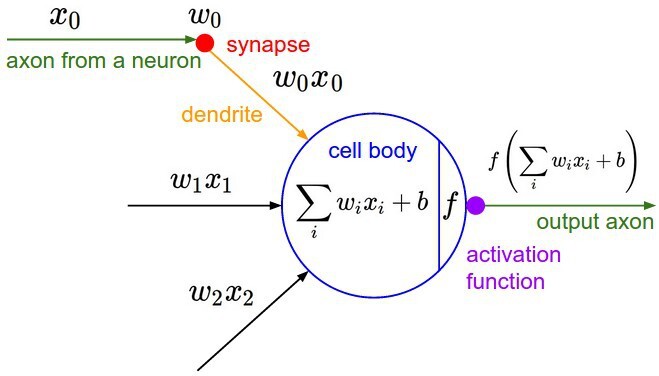
각각의 뉴런은 수상돌기(Dendrites)들로부터 입력신호를 수신하고 단일 축색돌기(Axon)를 따라 출력이 되게 되며 시냅스를 통해 다른 뉴런의 수상돌기에 연결되어 신호가 전달되게 됩니다.

이러한 모델에서 이동하는 신호(x0)는 해당 시냅스(w0)의 시냅스 강도에 기초하여 다른 뉴런의 수상돌기와 상호작용(x0 * w0)되어 새로운 input이 됩니다.

시냅스 강도(w)는 학습이 가능하며, 한 뉴런이 다른 뉴런에 대한 영향력의 강도(bias)를 흥분(+) 또는 억제(-)가 가능하다는 아이디어가 됩니다.

기본적인 모델에서는 수상돌기들은 그들이 합산되는 세포로 신호를 운반합니다.

전달받은 신호를 모아 최종 합계가 일정 한계치를 넘으면 뉴런이 발화되어 축색돌기를 따라 계산된 결과를 보낼 수 있습니다.

이를 통해 우측의 수학적 모델에서는 신호전달의 정확한 타이밍은 고려하지 않고 입력받은 신호를 발화하는 비율을 활성화함수(Activation Function) f로 모델화합니다.

전통적으로는 실수값을 입력받아 0-1의 범위로 output을 내는 sigmoid함수를 activation function으로 사용하였습니다.

하나의 뉴런의 역할에 해당하는 간단한 코드는 다음과 같습니다

이렇듯 하나의 뉴런은 특정 input에 대해 '발화'하거나 '비활성화'하는 능력을 갖고 있기 때문에 단일 뉴런을 하나의 Linear Classifier로 사용할 수도 있습니다

• Binary Softmax Classifier
• Binary SVM Classifier
• Regularization Interpretation

그러나 Sigmoid 함수를 Activation 함수로 사용함으로써 발생하는 문제와 다른 활성화 함수들은 따로 알아보도록 하겠습니다.