Activation Function

(과거 포스팅 내용으로 최근 내용과 다를 수 있습니다.)

Activation Function (non-linear function)은 뉴런에서 단일 입력값을 받아 특정 연산을 수행한 output을 출력하는 역할을 하며 주로 사용되는 활성화 함수를 소개하겠습니다.

1. Sigmoid
   
   $f(x) = \frac{1}{1+e^{x}}$
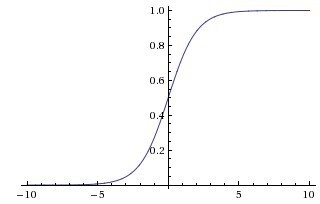
   Sigmoid 함수는 위 함수처럼 뉴런으로부터 실수의 값을 넘겨 받아 위와 같이 0-1사이의 값으로 넘겨줍니다.
   절대값이 큰 음수는 0, 절대값이 큰 양수는 1로 반환이 됩니다.
   이러한 Sigmoid 함수는 뉴런의 발화 (0->>비활성화, 1->>발화) 컨셉을 잘 나타낸 이유로 초기에는 많이 사용되었지만 현재는 아래와 같은 문제로 인해 다른 활성화 함수로 대체되었습니다.

• Gradient Vanishing
  Sigmoid의 매우 좋지 않은 특징은 뉴런의 활성화 값이 0 또는 1의 어느 한쪽 끝에서 포화될 때, 해당 지역의 경사(Gradient)는 거의 0이 된다는 점입니다.
  경사가 거의 0이 됨으로써 발생하는 문제는 각 파라미터의 cost 함수에서의 기울기를 구하는 역전파기법(Back-Propagation)에서 나타나는데 최종 output에서 앞쪽으로 뉴런을 거슬러 올라가면서 전달되는 값에 해당 뉴런의 활성화값의 기울기를 곱하게 됩니다.
  이러한 과정에서 활성화 값이 0 또는 1에 가까워 해당 기울기(local-gradient)가 매우 작은 값이라면 앞쪽의 가중치와 데이터에 전달되는 기울기를 소실시키게 되며 신경망의 layer의 깊이가 깊어질수록 이러한 문제는 더욱 심해지게 됩니다.
  게다가 이러한 이유로 활성화값이 가운데로 모이도록 가중치를 과도히 신중하게 초기화해야하는 문제 또한 발생합니다.

• Not zero-centered
  0중심이 아닌 Sigmoid의 함수값이 발생시키는 문제는 어떤 뉴런의 입력값(x)가 모두 양수라 가정하면 편미분의 Chain Rule에 의해 Loss함수(L)에 대한 파라미터 w의 Gradient는 다음과 같습니다.
  $(a = w^t*x + b)$
  $\frac{∂L}{∂w}=\frac{∂L\times∂a} {∂a\times∂w}$
  $\frac{∂a}{∂w}=x$
  $\frac{∂L}{∂w}=\frac{∂L}{∂a}\times x$
  즉 Parameter w의 Gradient는 입력값 x에 의해 영향을 받으며, 만약 입력값이 모두 양수라면 파라미터의 부호는 모두 같게 됩니다.
  이렇게 되면 Gradient Descent를 할 때 정확한 방향으로 가지 못하고 지그재그로 수렴하는 문제가 발생하게 됩니다.
  즉, Sigmoid 함수를 거친 활성화 값은 다음 레이어의 입력값이 되기 때문에 not zero-centered 특성의 Sigmoid는 학습에 부적합합니다.

2. Tanh
   
   $tanh(x)=2σ(2x)−1$
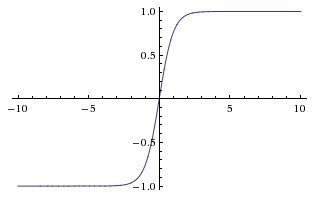
   Tanh 함수는 Sigmoid와 비슷한 모양이지만 -1과 1사이의 값을 리턴하여 zero-centered의 특성을 갖고있으며 Sigmoid보다 다양한 기울기를 표현할 수 있어 Sigmoid보다는 선호되는 활성화 함수입니다.

3. ReLU (Rectified Linear Unit)
   
   $f(x)=max(0,x)$
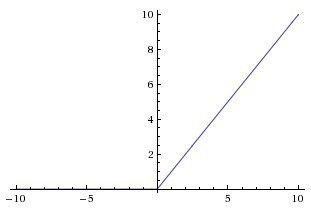
   ReLU함수는 현재까지 가장 많이 사용되는 활성화함수로써 위 식과 같이 단순히 0보다 작으면 0, 그보다 크면 x값을 그대로 리턴하는 매우 간단한 함수입니다.
   하지만 이러한 선형적 특징때문에 앞선 기울기소실문제가 줄어들며 sigmoid/tanh에 비해 수렴하는 속도가 빠르며 sigmoid/tanh의 비교적 복잡한 연산에 비해 max(0, x)의 단순한 계산으로 연산비용을 줄일 수 있는 장점이 있습니다.
   하지만 활성화함수로 ReLU를 사용하는 뉴런은 0이하의 수는 0으로 리턴하는 특성 때문에 한 번 비활성화된 뉴런은 학습이 끝날때까지 비활성화되는 경우가 발생합니다.
   예를 들어, 학습속도가 너무 높게 설정되어 있다면 파라미터가 자칫 dead-point로 빠지기 쉬워, 전체 뉴런의 40%는 죽은채 학습이 진행됩니다.
   이를 고려하여 적절한 학습률 설정으로 이러한 문제를 줄일 수 있습니다.
   하지만 이러한 문제점에도 현존하는 활성화 함수 중에서는 안정되고 높은 수렴 속도 때문에 많이 사용되는 활성화함수입니다.

4. Leaky ReLU
   
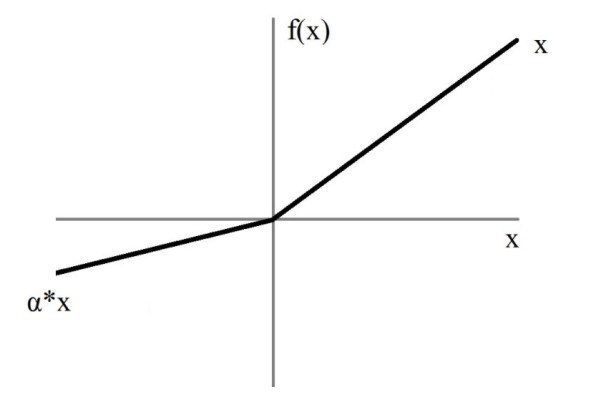
   f(x)=𝟙(x<0)(αx)+𝟙(x>=0)(x)
   Leaky ReLU함수는 위에서 다룬 ReLU의 뉴런이 죽는 문제를 해결하기 위해 탄생했습니다
   0이하의 수는 0으로 리턴하는 대신에 α(0.01 or so) 라는 수를 곱해 약간의 slope를 두어 리턴하게 됩니다.
   하지만 해당 함수가 잘 동작할 때도 있고 그렇지 않은 경우가 있어 일관성이 아직 증명되지 않았기 때문에 필요 시, 해결하고자하는 문제에 따라 적용하여 테스트가 필요합니다.

5. Maxout
   $max(w1 * x + b1, w2 * x + b2)$
   지금까지 다뤘던 활성화 함수의 functional form( f(w^tx + b) )과는 달리 ReLU, Leaky ReLU함수의 일반화된 형태의 함수로써 Maxout은 위의 수식처럼 ReLU의 선형적 특징의 양끝으로 포화하지 않는 장점을 가져감과 동시에 Leaky ReLU의 'Dead Neuron'문제를 해결하는 장점 또한 가져가는 활성화 함수입니다.
   하지만 하나의 뉴런에 기존의 두 배의 파라미터를 필요로 한다는 단점이 있습니다

Summary
ReLU 함수의 'Dead Neuron'문제를 고려한다면 'Leaky ReLU', 'Maxout' 사용을 고려해볼만 합니다.
또한 sigmoid 함수는 위에서 설명한 문제로 사용은 권장하지 않으며 굳이 사용을 원한다면 tanh 사용이 권장되지만 대부분의 경우에는 ReLU/Maxout 보다는 낮은 성능을 보여줍니다